This document describes the simulation of a quadrature mirror filter (QMF) bank using MATLAB software. It provides background on QMF banks, describing their use in signal processing applications like subband coding. The document then gives details on implementing a two-channel QMF bank in MATLAB, including generating the analysis and synthesis filters and processing a sample input signal through the filter bank. It concludes by showing the output of the MATLAB simulation and citing references.

1. ADVANCED DIGITAL
SIGNAL
PROCESSING
(CECNG-522)
13-07-2022 1

2. ‘SIMULATION OF QMF(QUADRATURE MIRROR FILTER)
BANK
USING MATLAB SOFTWARE
SUBMITTED TO:
PROF. DR. K . ANUSUDHA
SUBMITTED BY:
MOHAMMAD HANNAN(21304014)
M-TECH ELECTRONICS AND COMMUNICATION ENGINEERING
DEPARTMENT OF ELECTRONICS ENGINEERING
SCHOOL OF ENGINEERING AND TECHNOLOGY
PONDICHERRY UNIVERSITY , KALAPET
PUDUCHERRY-605014
13-07-2022 2

3. Quadrature-Mirror Filter
Bank
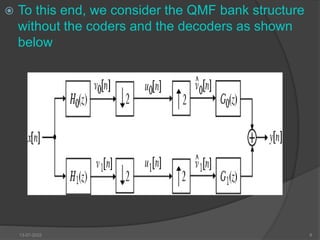
 In many applications, a discrete-time signal x[n] is
split into a number of sub-band signals by
means of an analysis filter bank
 The sub-band signals are then processed
 Finally, the processed sub-band signals are combined
by a synthesis filter bank resulting in an output signal
y[n]
 If the sub-band signals are band limited to
frequency ranges much smaller than that of the
original input signal x[n], they can be down-sampled
before processing
 Because of the lower sampling rate, the processing of
the down-sampled signals can be carried out more
efficiently
]}
[
{ n
vk
]}
[
{ n
vk
13-07-2022 3

4.  After processing, these signals are then up-sampled
before being combined by the synthesis filter bank
into a higher-rate signal
 The combined structure is called a quadrature-mirror
filter (QMF) bank
 If the down-sampling and up-sampling factors are
equal to or greater than the number of bands of the
filter bank, then the output y[n] can be made to retain
some or all of the characteristics of the input signal
x[n] by choosing appropriately the filters in the
structure
 If the up-sampling and down-sampling factors are
equal to the number of bands, then the structure is
called a critically sampled filter bank
 The most common application of this scheme is in the
efficient coding of a signal x[n]
13-07-2022 4

5. Two-Channel QMF Bank
 Figure below shows the basic two-channel QMF
bank-based subband codec (coder/decoder)
The analysis filters and have typically a low-pass
and high-pass frequency responses, respectively, with a cutoff at
p/2
)
(z
H0
)
(z
H1
13-07-2022 5

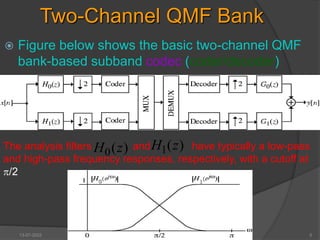
6.  Each down-sampled subband signal is encoded
by exploiting the special spectral properties of the
signal, such as energy levels and perceptual
importance
 It follows from the figure that the sampling rates of
the output y[n] and the input x[n] are the same
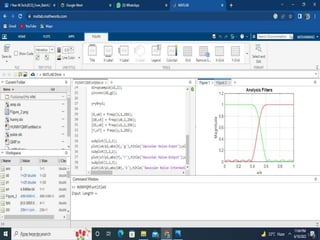
 The analysis and the synthesis filters are chosen
so as to ensure that the reconstructed output y[n]
is a reasonably close replica of the input x[n]
 Moreover, they are also designed to provide good
frequency selectivity in order to ensure that the
sum of the power of the subband signals is
reasonably close to the input signal power
13-07-2022 6

7.  In practice, various errors are generated in this
scheme
 In addition to the coding error and errors caused
by transmission of the coded signals through the
channel, the QMF bank itself introduces several
errors due to the sampling rate alterations and
imperfect filters
 We ignore the coding and the channel errors
 We investigate only the errors caused by the
sampling rate alterations and their effects on the
performance of the system
13-07-2022 7

8.  To this end, we consider the QMF bank structure
without the coders and the decoders as shown
below
13-07-2022 8

9. Analysis of the Two-Channel
QMF Bank
 Making use of the input-output relations of the
down-sampler and the up-sampler in the z-domain
we arrive at
 From the first and the last equations we obtain
after some algebra
),
(
)
(
)
( z
X
z
H
z
V k
k 
)},
(
)
(
{
)
( /
/ 2
1
2
1
2
1
z
V
z
V
z
U k
k
k 


)
(
)
( 2
z
U
z
V k
k 
)}
(
)
(
{
)
( z
V
z
V
z
V k
k
k 


2
1
)}
(
)
(
)
(
)
(
{ z
X
z
H
z
X
z
H k
k 



2
1
^
k = 0, 1
^
13-07-2022 9

10.  The reconstructed output of the filter bank is given
by
 From the two equations of the previous slide we
arrive at
 The second term in the above equation is due to
the aliasing caused by sampling rate alteration
)
(
)
(
)
(
)
(
)
( z
V
z
G
z
V
z
G
z
Y 1
1
0
0 

^ ^
)
(
)}
(
)
(
)
(
)
(
{
)
( z
X
z
G
z
H
z
G
z
H
z
Y 1
1
0
0
2
1


)
(
)}
(
)
(
)
(
)
(
{ z
X
z
G
z
H
z
G
z
H 



 1
1
0
0
2
1
13-07-2022 10

11.  The input-output equation of the filter bank can be
compactly written as
 where T(z), called the distortion transfer function,
is given by
 And
)
(
)
(
)
(
)
(
)
( z
X
z
A
z
X
z
T
z
Y 


)}
(
)
(
)
(
)
(
{
)
( z
G
z
H
z
G
z
H
z
T 1
1
0
0
2
1


)}
(
)
(
)
(
)
(
{
)
( z
G
z
H
z
G
z
H
z
A 1
1
0
0
2
1




13-07-2022 11

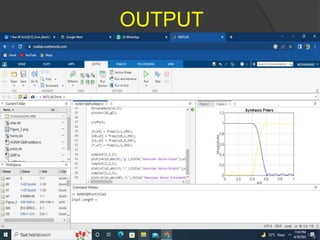
12. MATLAB CODE
 [N,fpts,mag,wt]=firpmord([0.395 0.605],[1 0],[0.0005
0.0005]);[q,err]=firpm(N,fpts,mag,wt);q(18)=q(18)+err;h0=firminphase(q)
;g0=fliplr(h0);k=0:17;h1=((-1).^k).*g0;g1=-((-1).^k).*h0;[H0,w0] =
freqz(h0,1,256);[H1,w1] = freqz(h1,1,256);[G0,w2] =
freqz(g0,1,256);[G1,w3] =
freqz(g1,1,256);plot(w0/pi,abs(H0),'g',w1/pi,abs(H1),'r'),title('Analysis
Filters');xlabel('omega/pi');
ylabel('Magnitude');grid;figure;plot(w2/pi,abs(G0),'b',w3/pi,abs(G1),'y'),titl
e('Synthesis Filters');grid;xlabel('omega/pi'); ylabel('Magnitude');m =
input('Input Length =
');x=randn(1,m);v0=conv(h0,x);u0=downsample(v0,2);d0=upsample(u0,
2);y0=conv(d0,g0);v1=conv(h1,x);u1=downsample(v1,2);d1=upsample(u
1,2);y1=conv(d1,g1);y=y0+y1;[X,w4] = freqz(x,1,256);[U0,w5] =
freqz(u0,1,256);[U1,w6] = freqz(u1,1,256);[Y,w7] =
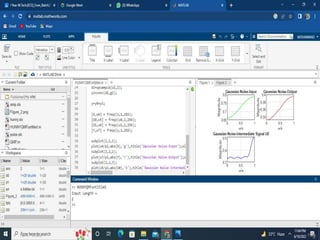
freqz(y,1,256);subplot(2,2,1);plot(w4/pi,abs(X),'g'),title('Gaussian Noise-
Input');xlabel('omega/pi');
ylabel('Magnitude');grid;subplot(2,2,2);plot(w7/pi,abs(Y),'r'),title('Gaussia
n Noise-Output');xlabel('omega/pi');
ylabel('Magnitude');grid;subplot(2,2,3);plot(w5/pi,abs(U0),'b'),title('Gaussi
an Noise-Intermediate Signal U0');xlabel('omega/pi');
ylabel('Magnitude');grid;
13-07-2022 12

13. OUTPUT
13-07-2022 13

14. 13-07-2022 14

15. 13-07-2022 15

16. REFERENCES
 Gershenfeld, Neil (1998), The Nature of
Mathematical Modeling, Cambridge,
England: Cambridge University Press, pp.
132–135, ISBN 0521570956
 Design of Quadrature Mirror filter banks
using complex half-band filters-
https://ieeexplore.ieee.org/document/59574
13
 Quadrature mirror filter bank--
https://slideplayer.com/slide/15977224/
13-07-2022 16

17. THANK
YOU
13-07-2022 17