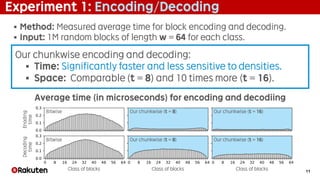
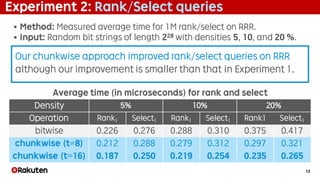
The document presents a study on faster practical block compression techniques for rank/select dictionaries, which are crucial for analyzing large volumes of web log data. It introduces a new chunkwise processing approach that improves encoding and decoding time while maintaining a competitive space efficiency compared to existing methods. Experimental results highlight the advancements in speed and stability of the proposed method over traditional blockwise and bitwise approaches.

1. Faster Practical Block Compression
for Rank/Select Dictionaries
Yusaku Kaneta | yusaku.kaneta@rakuten.com
Rakuten Institute of Technology, Rakuten, Inc.

2. 2
Background
§ Compressed data structures in Web companies.
• Web companies generate massive amount of logs in text formats.
• Analyzing such huge logs is vital for our decision making.
• Practical improvements of compressed data structures are important.
§ RRR compression [Raman, Raman, Rao, SODA’02]
• Basic building block in many compressed data structures.
• Rank/Select queries on compressed bit strings in constant time:
‣ Rankb(B, i): Number of b’s in B’s prefix of length i.
‣ Selectb(B, i): Position of B’s i-th b.
B is an input bit string
b: a bit in {0, 1}

3. 3
RRR = Block compression + succinct index
§ Represents a block B of w bits into a pair (class(B), offset(B)).
• class(B): Number of ones in B.
• offset(B): Number of preceding blocks of class same as B for some
order (e.g., lexicographical order of bit strings).
§ log w bits for class(B) and log2
w
class(B)
bits for offset(B).
§ Two practical approaches to block compression:
• Blockwise approach [Claude and Navarro, SPIRE’09]
• Bitwise approach [Navarro and Providel, SEA’12]

4. 4
Block compression in practice
Good: O(1) time.
Bad: Low compression ratio.
§The tables limit use of larger w.
§log w bits for class(B) become non-
negligible.
§Ex) 25% overhead for w = 15.
1. Blockwise approach
[Claude and Navarro, SPIRE’09]
2. Bitwise approach
[Navarro and Providel, SEA’12]
Idea: O(2ww)-bit universal tables. Idea: O(w3)-bit binomial coefficients.
Good: High compression ratio.
Bad: O(w) time.
§Count bit strings lexicographically
smaller than block B bit by bit.
§In practice, heuristics of encoding
and decoding blocks with a few
ones in O(1) time can be used.
Less flexible in practice

5. 5
Main result
§ Practical encoder/decoder for block compression
• Generalization of existing blockwise and bitwise approaches.
• Idea: chunkwise processing with multiple universal tables.
• Faster and more stable on artificial data.
Method Encode Decode Space (in bits)
Blockwise [Claude and Navarro, SPIRE’09] O(1) O(1) O(2ww)
Bitwise [Navarro and Provital, SEA’12] O(w) O(w) O(w3)
Chunkwise (This work) O(w/t) O((w/t) log t) O(w3 + 2t t)
This talk uses w and t for block and chunk lengths, respectively.

6. 6
Our algorithm

7. 7
Overview of our algorithm
§ Main idea: Process a block B in a chunkwise fashion.
• Bi: The i-th chunk of length t. (Suppose t divides w.)
‣ Encoded/Decoded in O(1) time using O(2tt)-bit universal tables.
• Efficiently count up blocks X satisfying X < B by using a combination
formula and chunkwise order:
A lexicographical order with:
1. class(Xi) < class(Bi) or
2. class(Xi) = class(Bi) and offset(Xi) < offset(Bi)
t
c
×
n − t
m − c
c m − c
n − tt
Number of ones:
Number of bits:
Block X
Combination formula: Chunkwise order: X < B

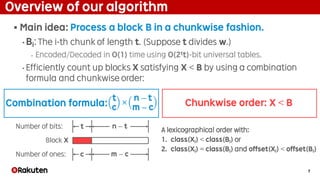
8. 8
Block encoding in O(w/t) time
Lemma: Block encoding can be implemented in
O(w/t) time with O(w3+2tt)-bit universal tables.
` 1
oi+1
B0···Bi-1
oi
2
X[0, i) X[i] •••
Blocks X of class same as B
in descending order of offset(X)
from top to bottom.
oi = X X0···Xi-1 < B0···Bi-1
ci
ni
class(B)
− ci − class(Bi)
w − ni − t#bits
#ones
Bi Bi+1···Bw/t-1
• w− ni − t is in {0, t, 2t, …, (w/t)t=w}.
• class(B) − ci − c ranges in [0, w).
• class(Bi) ranges in [0, t).
• Each value can be represented in w bits.
2. class(Xi) = class(Bi) and offset(Xi) < offset(Bi)
Idea:
Multiplication
offset(Bi)×
w − ni − t
class(B) − ci − class(Bi)
1. class(Xi) < class(Bi):
Idea:
Summation
%
t
c
×
w − ni − t
class(B) − ci − c
class(Bi)&1
c = 0

9. 9
Block decoding in O((w/t)log t) time
§ Reverse operation of block encoding.
• class(Bi): O(log t) time by a successor query on a universal table.
• offset(Bi): O(1) time by integer division.
min k ∑ t
c
×
w − ni − t
class(B) − ci − c
≥ offset(B) − oi
k
c = 0
Lemma: Block decoding can be implemented in
O((w/t)log t) time with O(w3+2tt)-bit universal tables.
Idea:
Successor
query

10. 10
Experimental results

11. 11
Experiment 1: Encoding/Decoding
§ Method: Measured average time for block encoding and decoding.
§ Input: 1M random blocks of length w = 64 for each class.
Our chunkwise encoding and decoding:
§ Time: Significantly faster and less sensitive to densities.
§ Space: Comparable (t = 8) and 10 times more (t = 16).
Average time (in microseconds) for encoding and decodiing
Bitwise
Bitwise
Our chunkwise (t = 8)
Our chunkwise (t = 8)
Our chunkwise (t = 16)
Our chunkwise (t = 16)
Class of blocks Class of blocks Class of blocks
Decoding
time
Enoding
time

12. 12
Experiment 2: Rank/Select queries
§ Method: Measured average time for 1M rank/select on RRR.
§ Input: Random bit strings of length 228 with densities 5, 10, and 20 %.
Density 5% 10% 20%
Operation Rank1 Select1 Rank1 Select1 Rank1 Select1
bitwise 0.226 0.276 0.288 0.310 0.375 0.417
chunkwise (t=8) 0.212 0.288 0.279 0.312 0.297 0.321
chunkwise (t=16) 0.187 0.250 0.219 0.254 0.235 0.265
Average time (in microseconds) for rank and select
Our chunkwise approach improved rank/select queries on RRR
although our improvement is smaller than that in Experiment 1.

13. 13
Conclusion
§ Practical block encoding and decoding for RRR
• New time-space tradeoff based on chunkwise processing:
‣ O(w/t) encoding
‣ O((w/t)log t) decoding
‣ O(w3 + 2tt) bits of space.
• Generalize previous blockwise and bitwise approaches.
• Fast and stable on artificial data with various densities.
§ Future work:
• More experimental evaluation on real data.

14. THANK YOU