Our techniques provide fast wavelet tree construction in practice based on recent theoretical work. Experiments on real datasets show our methods using the PEXT and PSHUFB CPU instructions outperform previous approaches. For wavelet trees, our methods are 1.9x faster than naive construction on average and competitive with state-of-the-art. For wavelet matrices, we achieve speedups of 1.1-1.9x over the state-of-the-art. This work provides the first practical implementation of the fastest known wavelet tree construction algorithms.

1. Fast Wavelet Tree Construction
in Practice
2018/10/10
Yusaku Kaneta
Rakuten Institute of Technology
Rakuten, Inc.

2. 2
Background
§ Wavelet tree [Grossi+,SODA’03] / Wavele matrix [Claude+,SPIRE’12]
• Fundamentaltoolsinmodernstringprocessing.
• Fastaccess,rank,andselectonanarrayofnintegersin[0,σ).
10 1 1 0 1 1 000 10 10 01
11 0 01 1 0100 11 00 0 1
1 0 100 01 1 00 0 11 1 10
00 101 10 1 10 1 01 00 1
Awavelettreeson[6,8,9,4,14,11,1,0,5,7,12,13,15,2,3,10]

3. 3
Fast WT construction has attracted much attension!!
Papers
Sequential?
Parallel?
Impl.?
[Fuentes-Sepúlveda+,SEA’14] P Yes
[Shun+,DCC’15] P Yes
[Labeit+,DCC’16] P Yes
[Fischer+,ALENEX’18] S+P Yes
[Munro+,SPIRE’14][Babenko+,SODA’15](Bestupperbound) S No
[Shun+,DCC’17](Bestupperbound) P No
§ Gap between theory and practice:
• Nopracticalimplementationof[Munro+,SPIRE’14][Babenko+,
SODA’15]:Thecurrentfastestwavelettreeconstructionalgorithm.

4. 4
First* practical implementation of wavelet tree construction
based on [Munro+, SPIRE’14][Babenko+, SODA’15]
Main result
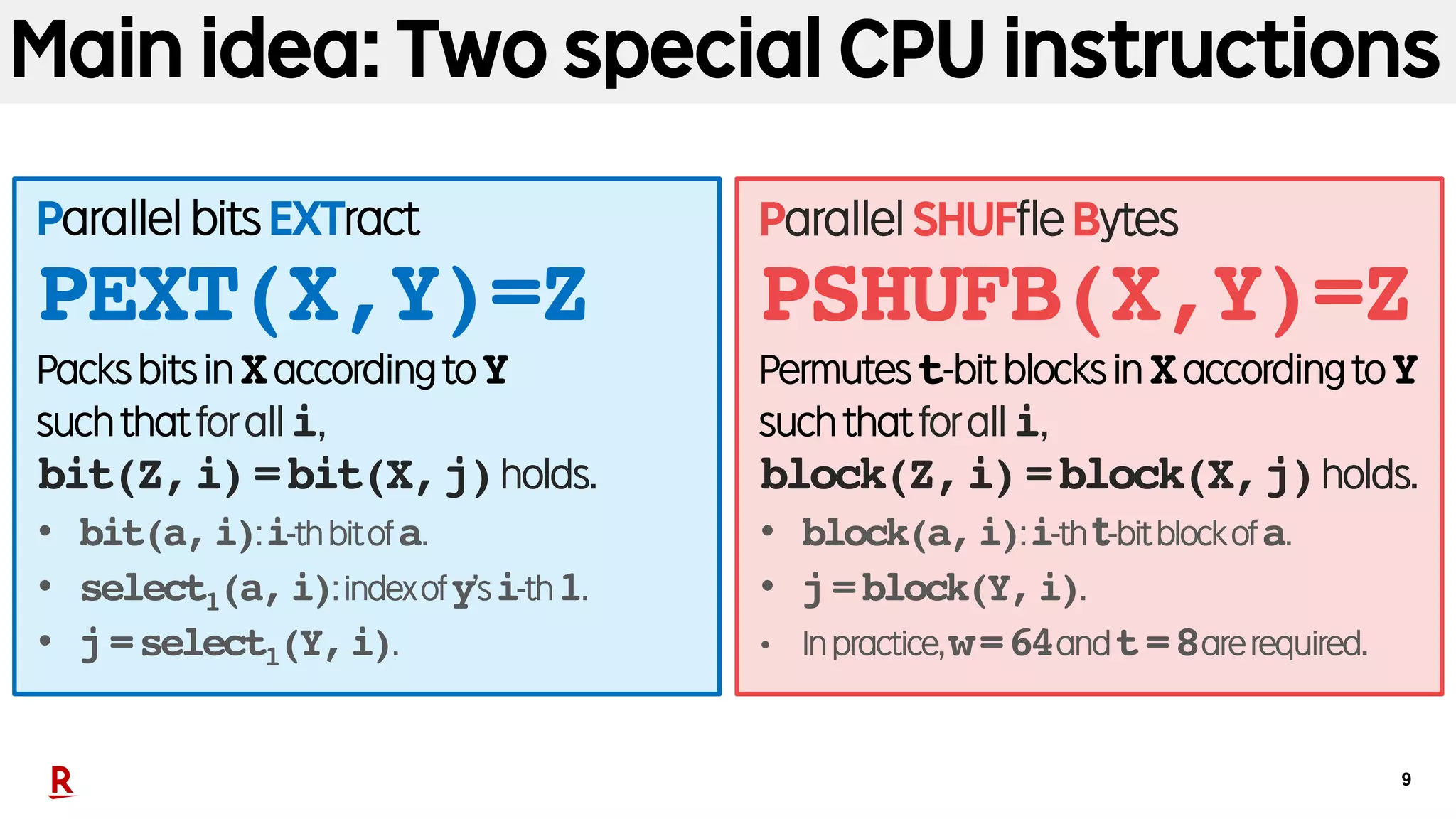
§ Our idea: Replace precomputed tables w/
• SpecialCPUinstruction:PEXTin(BMI2)orPSHUFB(inSSSE3).
• Broadwordcomputation(omitted).
§ Experiments on real datasets:
• Wavelettree:ourswerecompetitivetoSOTA[Fischer+,ALENEX'18]
• Waveletmatrix:ourswere1.1–1.9xfasterthanSOTA.
*SzymonGrabowskikindlypointedthatTuukkaNorrialsotriedsimilarapproaches:
github.com/tsnorri/wt-construct-gn

5. 5
Our Techniques
for Practical Implementation

6. 6
Basic construction of wavelet trees
§ Recursivelysplita(sub)arrayofelements
accordingtotheiri-thtargetbits.
• Processoneelementatatime.
• Appenditstargetbittoabitvector.
• Appendittotheleft(resp.,right)subarray
ifitstargetbitis0(resp.,1).
Assumewordlengthw = 32,inputintegerwidtht =4,andthusw/t = 8 forexplanation.
6
0110
8
1000
9
1001
4
0100
14
1110
11
1011
1
0001
0
0000
5
0101
7
0111
12
1100
15
1111
13
1101
2
0010
3
0011
10
1010

7. 7
Basic construction of wavelet trees
§ Recursivelysplita(sub)arrayofelements
accordingtotheiri-thtargetbits.
• Processoneelementatatime.
• Appenditstargetbittoabitvector.
• Appendittotheleft(resp.,right)subarray
ifitstargetbitis0(resp.,1).
Assumewordlengthw = 32,inputintegerwidtht =4,andthusw/t = 8 forexplanation.
6
0110
8
1000
9
1001
4
0100
14
1110
11
1011
1
0001
0
0000
5
0101
7
0111
12
1100
15
1111
13
1101
2
0010
3
0011
10
1010

8. 8
6
0110
8
1000
9
1001
4
0100
14
1110
11
1011
1
0001
0
0000
5
0101
7
0111
12
1100
15
1111
13
1101
2
0010
3
0011
10
1010
6
0110
8
1000
9
1001
4
0100
14
1110
11
1011
1
0001
0
0000
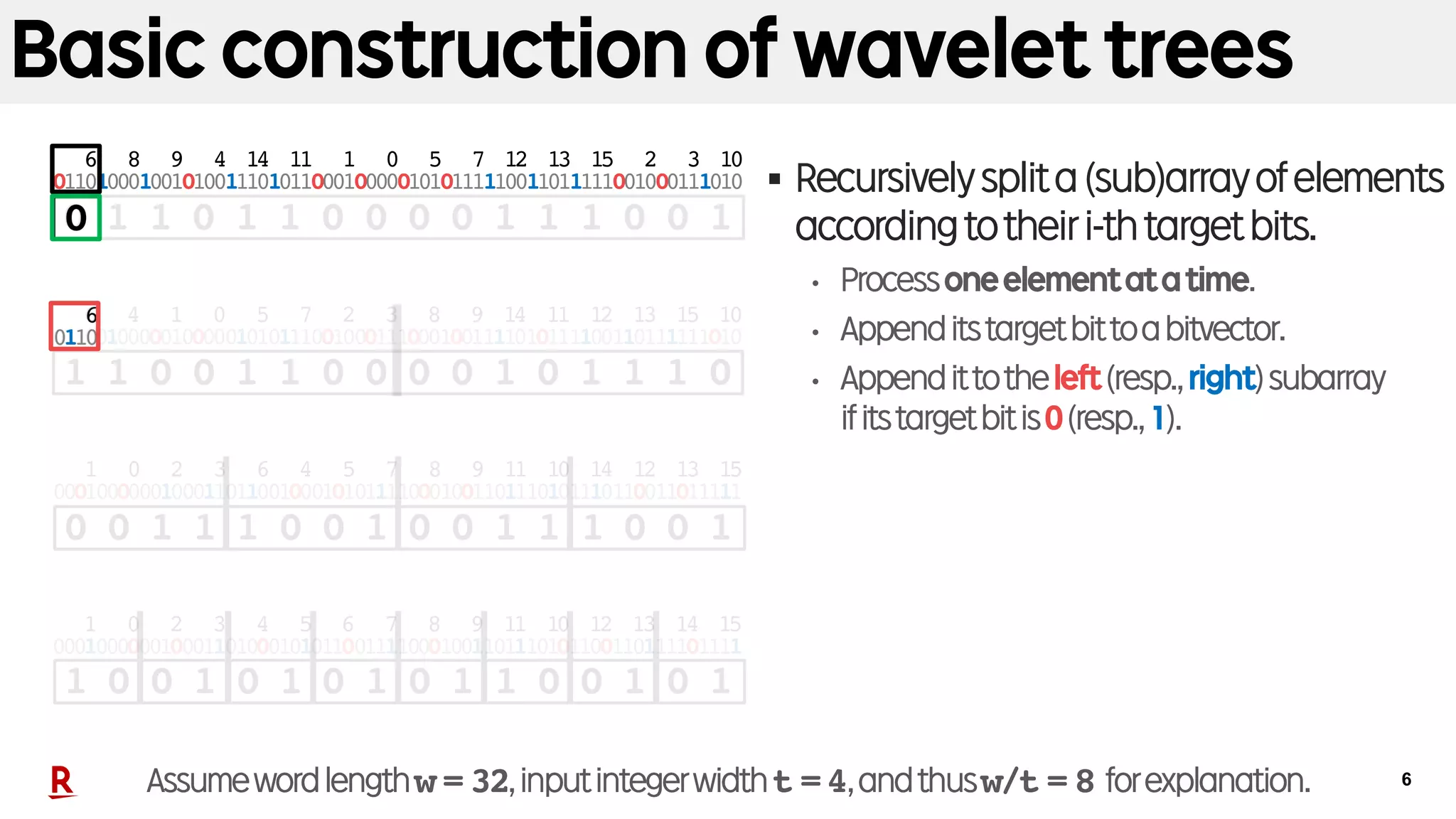
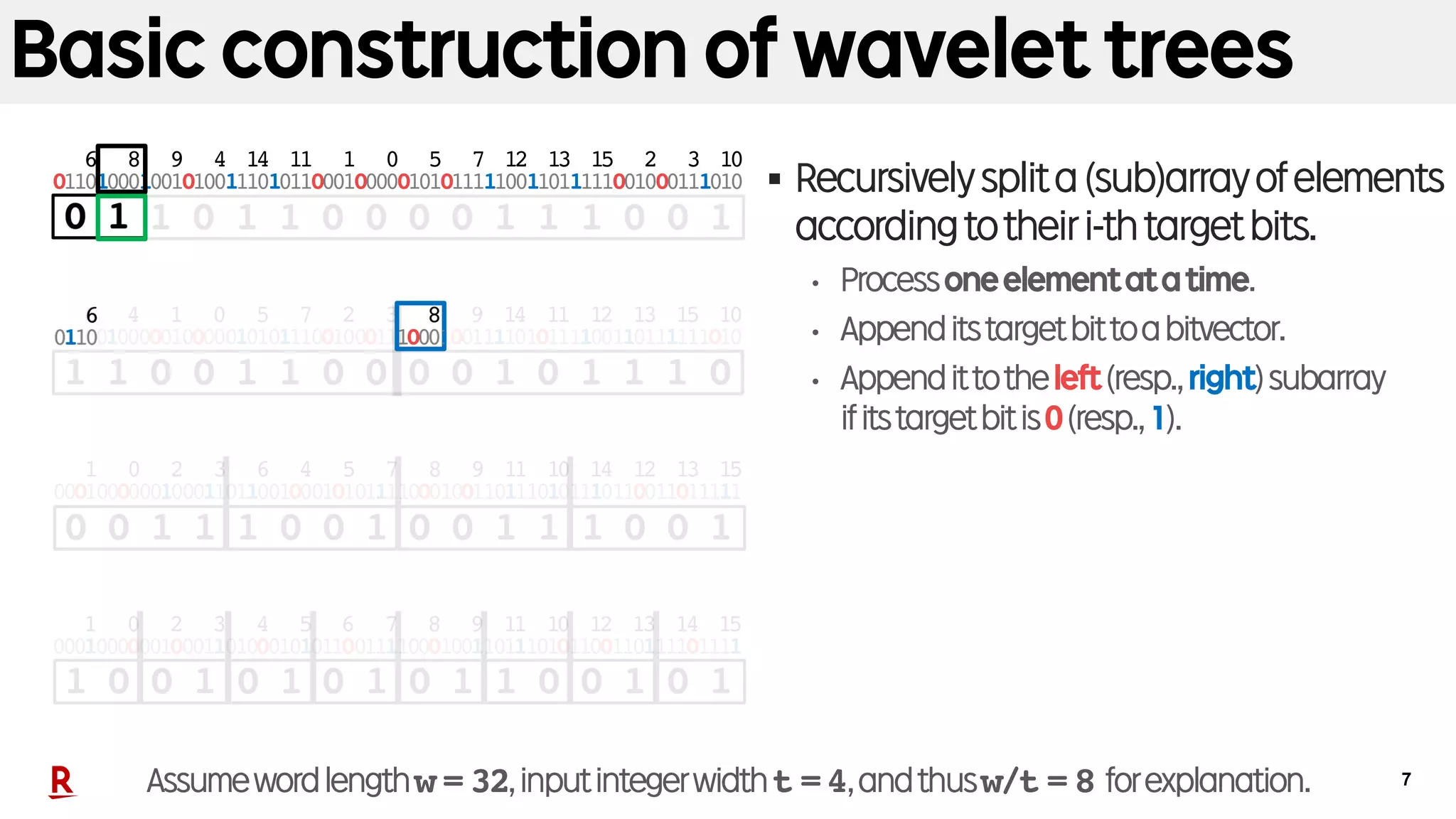
Fast construction of wavelet trees
§ Fastwavelettreeconstruction
[Munro+, SPIRE’14][Babenko+,SODA’15]
• Processmultipleelementsatatime.
• w/toft-bitelementscanbereadtogether.
§ Primitiveoperations:
X Bbitpack ( ,i)=
X X0listsplit( ,i)=( , )X1
X1
A subarray consisting of
X’s elements whose 0th bit 1
A subarray consisting of
X’s elements whose 0th bit 0
X0
First w/t elements in a word of w bits (e.g., w = 32 and t = 4)
X
Packed 0th bits of elements contained in X.
B
Assumewordlengthw = 32,inputintegerwidtht =4,andthusw/t = 8 forexplanation.
Assumption:
• ThestandardwordRAM
• w:wordlength(inbits)
• t:inputintegerwidth(inbits)
• t≤w justforexplanation.
(Thisconditioncanbeeliminated.)

9. 9
Main idea: Two special CPU instructions
ParallelbitsEXTract
PEXT(X,Y)=Z
PacksbitsinXaccordingtoY
suchthatforalli,
bit(Z,i)=bit(X,j)holds.
• bit(a,i):i-thbitofa.
• select1(a,i):indexofy’si-th1.
• j=select1(Y,i).
ParallelSHUFfleBytes
PSHUFB(X,Y)=Z
Permutest-bitblocksinXaccordingtoY
suchthatforalli,
block(Z,i)=block(X,j)holds.
• block(a,i):i-tht-bitblockofa.
• j=block(Y,i).
• Inpractice,w=64andt=8arerequired.

10. 10
PEXT-based technique for bitpack
§ Preprocessing:
• L: Packedarraywithblock(L,i) = 1foreveryiin[0,w/t)
(i.e.,eacht-bitblockhas1onlyatitslowestbit).
Assumewordsizew = 32,elementsizet =4,andthusw/t = 8 forexplanation.
01100100000100000101011100100011
00011001000001000001010111001000
>>t-i-1
00011001000001000001010111001000
00010001000100010001000100010001L
Z
Y
Y
X
11001100000000000000000000000000
1. Shift X by t-i-1=2 2. Perform PEXT(Y,L)=Z
PEXT(Y,L)
bitpack(X= ,i=1):01100100000100000101011100100011
6 4 1 0 5 7 2 3

11. 11
PEXT-based technique for listsplit
§ Preprocessing:
• H: Packedarraywithblock(H,i) = 2t-1foreveryiin[0,w/t)
(i.e.,eacht-bitblockhas1onlyatitshighestbit).
2. Perform PEXT(X,M1)=Z1 w/
M1=~M0
6 4 01 2 3
0 0 046 05 7
f f 0ff 00 0
75
M1
Z1
X
1. Perform PEXT(X,M0)=Z0 w/
M0=(H-((X>>(t-i-1))&L)^H)^H
0 0 f00 ff f
6 4 701 5 2 3
0 0 001 02 3
M0
Z0
X
listsplit(X= ,i=1):
PEXT(X, M0) PEXT(Z, M1)
6 4 701 5 2 3
01100100000100000101011100100011
Assumewordsizew = 32,elementsizet =4,andthusw/t = 8 forexplanation.
01100100000100000101011100100011 01100100000100000101011100100011

12. 12
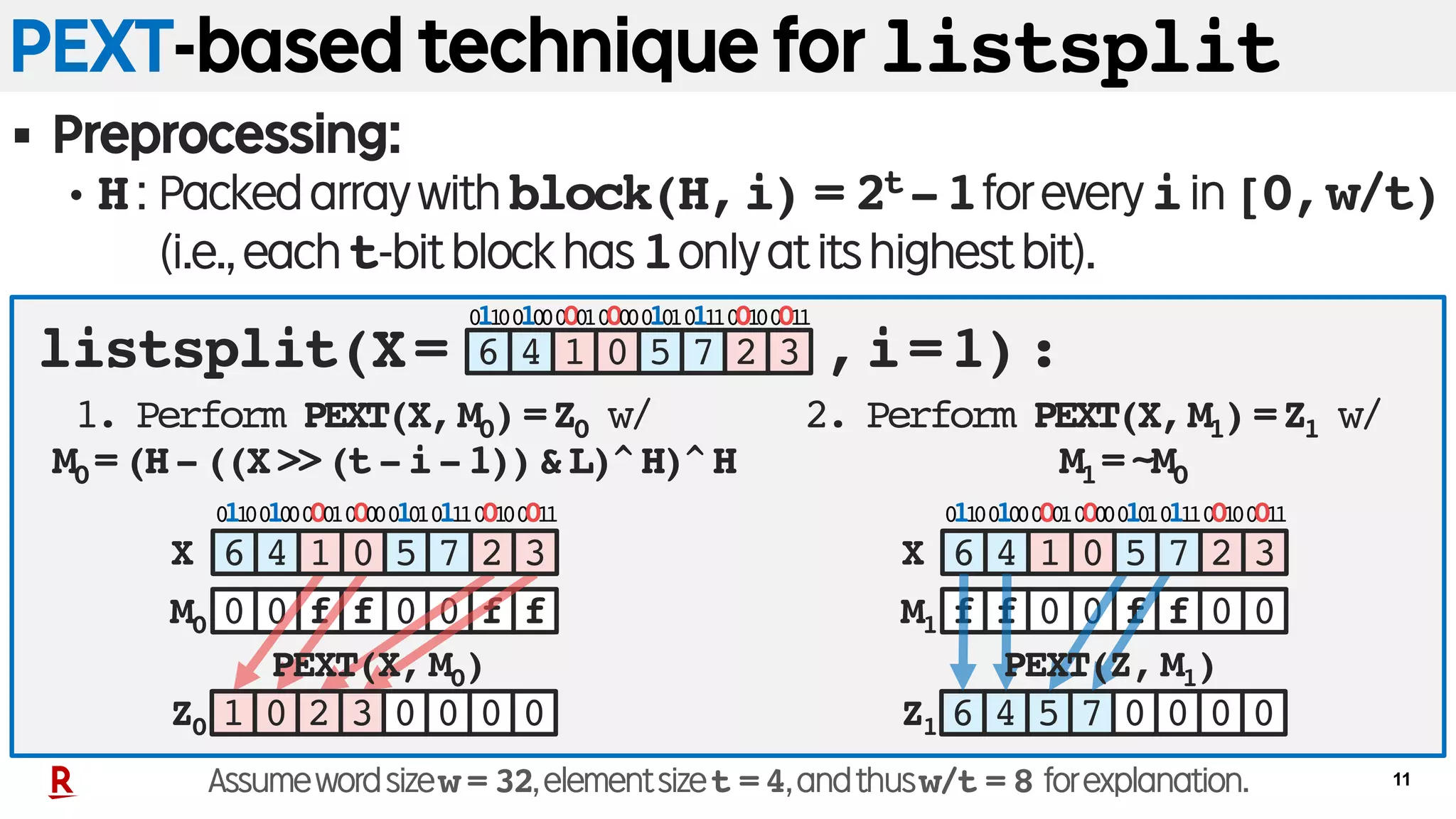
PSHUFB-based technique for listsplit
§ Preprocessing: Let m=2w/t be # of blocks in a word.
• T[a]forallain[0,m):Packedarraycontaininginascendingorder
(1)allindexesof0’sfollowedby(2)allindexesof1’sin a.
2. Extract each part from Y.
|a|1: Number of ones in a.
<<t|a|1
6 4 701 52 3
0 0 001 02 3Z0
Y 6 4 701 52 3
0 0 046 05 7Z1
Y
00010000001000110110010001010111 00010000001000110110010001010111
1. Perform PSHUFB(X,T[a]) w/
a=bitpack(X,i)=11001100
0 1 532 46 7
01100100000100000101011100100011
6 4 701 5 2 3
6 4 701 52 3
T[a]
Y
X
Assumewordsizew = 32,elementsizet =4,andthusw/t = 8 forexplanation.
>>t|a|1
<<w-t|a|1PSHUFB(X,T[a])
6 4 701 5 2 3
01100100000100000101011100100011
listsplit(X= ,i=1):

13. 13
Experiments

14. 14
Experimental setup and data
§ Setup:
• Corei7-4790(3.6GHz)w/16GBmainmemoryrunningUbuntu18.04.
§ Data:
• 6and10datasetsfromPizzaandChilliandLightweightCorpus,resp.
§ Methods:
• PSHUFB:ourmethodbasedonPSHUFBinstructioninSSSE3.
• PEXT:ourmethodbasedonPEXTinstructioninBMI2.
• NAÏVE,PS,PC:previousones(availableatgithub.com/kurpicz/pwd)
bitpackwas implemented by PEXT in allour methods.

15. 15
Result: wavelet tree
§ PSHUFB vs.NAÏVE:
• 1.9x(average)
§ PEXT vs.NAÏVE:
• 1.9x(average)
§ Oursv.s.PC/PS:
• Competitive
1st winner
2nd winner
Medianof5elapsedtimes(insec)forconstructing
awavelettreewithoutrankandselectindexes.
n σ NAÏVE PC PS PSHUFB PEXT
dblp.xml 2.96·108 97 5.57 2.99 3.03 3.09 3.04
dna 4.04·108 16 4.43 2.42 2.72 2.07 2.05
english 2.21·109 238 53.0 27.2 28.8 23.7 23.5
pitches 5.58·107 132 1.25 0.685 0.812 0.576 0.570
proteins 1.18·109 27 16.1 8.29 8.67 9.27 9.12
sources 2.11·108 229 4.94 2.54 2.61 2.37 2.55
chr22.dna 3.46·107 5 0.233 0.143 0.188 0.157 0.156
etext99 1.05·108 145 2.32 1.31 1.62 1.16 1.14
gcc-3.0.tar 8.66·107 149 1.91 1.32 1.12 0.949 0.935
howto 3.94·107 196 0.832 0.478 0.496 0.438 0.432
jdk13c 6.97·107 113 1.30 0.708 0.789 0.829 0.755
linux-
2.4.5.tar
1.16·108 255 2.76 1.41 1.45 1.30 1.51
rctail96 1.15·108 93 2.25 1.18 1.20 1.19 1.17
rfc 1.16·108 120 2.28 1.25 1.27 1.20 1.19
sprot34.dat 1.10·108 66 2.12 1.14 1.36 1.13 1.13
w3c2 1.04·108 255 2.30 1.30 1.28 1.30 1.18
OurPSHUFB andPEXT outperformedNAÏVE whilebeingcompatiblewithPC.

16. 16
Result: wavelet matrix
§ PSHUFB vs.NAÏVE:
• 3.0–4.6x
§ PEXT vs.NAÏVE:
• 2.5–4.5x
§ Oursv.s.PC:
• 1.1–1.9x
1st winner
2nd winner
n σ NAÏVE PC PS PSHUFB PEXT
dblp.xml 2.96·108 97 6.20 3.00 3.01 2.02 2.05
dna 4.04·108 16 5.88 2.43 2.70 1.29 1.30
english 2.21·109 238 57.0 27.2 28.5 15.8 15.9
pitches 5.58·107 132 1.37 0.684 0.709 0.429 0.547
proteins 1.18·109 27 22.4 8.29 8.41 6.36 6.43
sources 2.11·108 229 5.81 2.54 2.95 1.57 1.59
chr22.dna 3.46·107 5 0.385 0.143 0.164 0.130 0.092
etext99 1.05·108 145 3.01 1.27 1.34 0.803 0.771
gcc-3.0.tar 8.66·107 149 2.18 1.05 1.29 0.633 0.639
howto 3.94·107 196 1.011 0.478 0.494 0.295 0.298
jdk13c 6.97·107 113 1.57 0.708 0.705 0.500 0.506
linux-
2.4.5.tar
1.16·108 255 3.14 1.41 1.64 0.872 1.11
rctail96 1.15·108 93 2.37 1.22 1.19 0.779 0.792
rfc 1.16·108 120 2.65 1.30 1.28 0.791 0.811
sprot34.dat 1.10·108 66 2.81 1.14 1.38 0.905 0.855
w3c2 1.04·108 255 2.63 1.54 1.27 0.80 0.81
Medianof5elapsedtimes(insec)forconstructing
awaveletmatrixwithoutrankandselectindexes.
Our PSHUFB and PEXT outperformed all others: NAÏVE, PS, and PC.

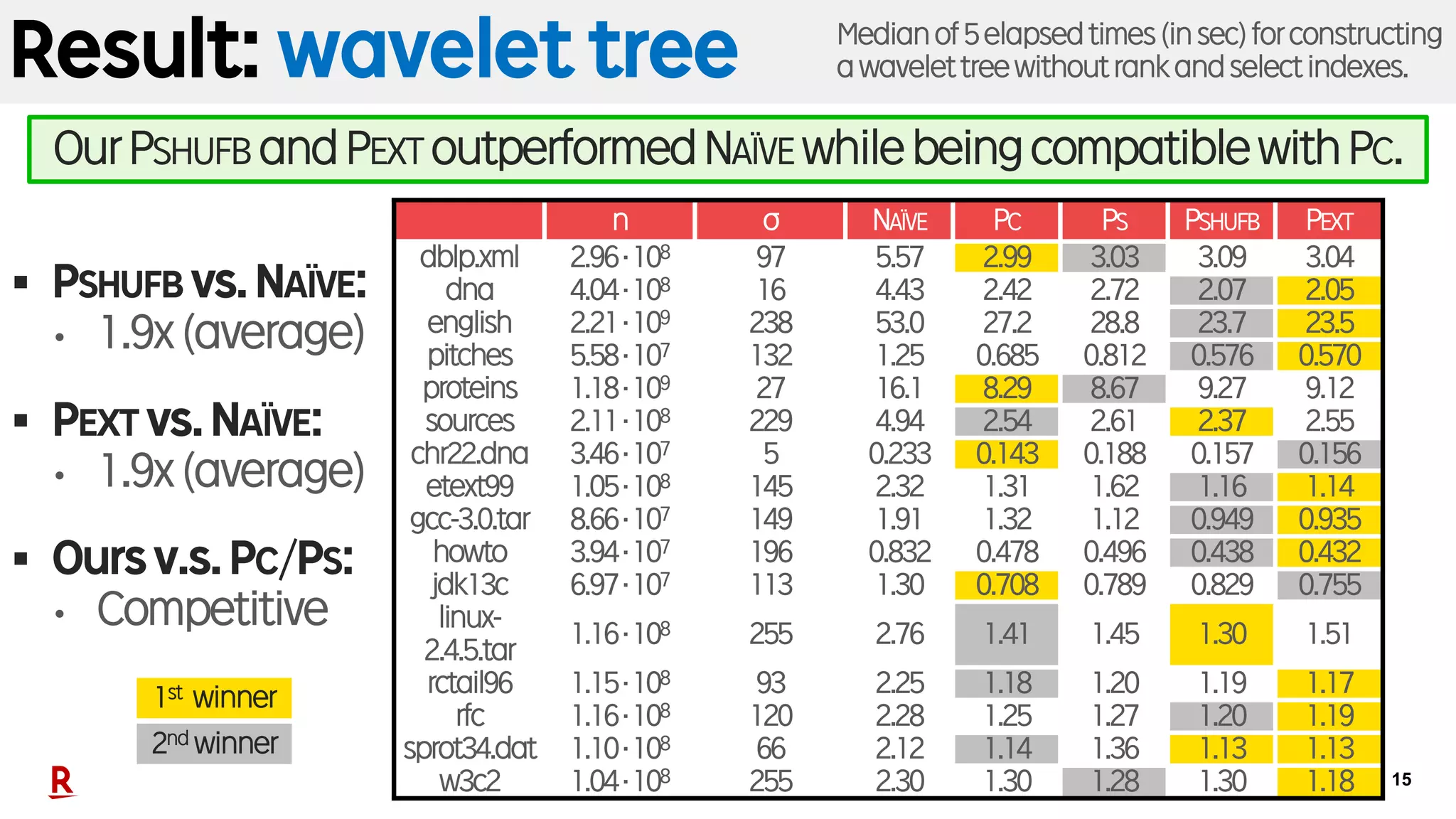
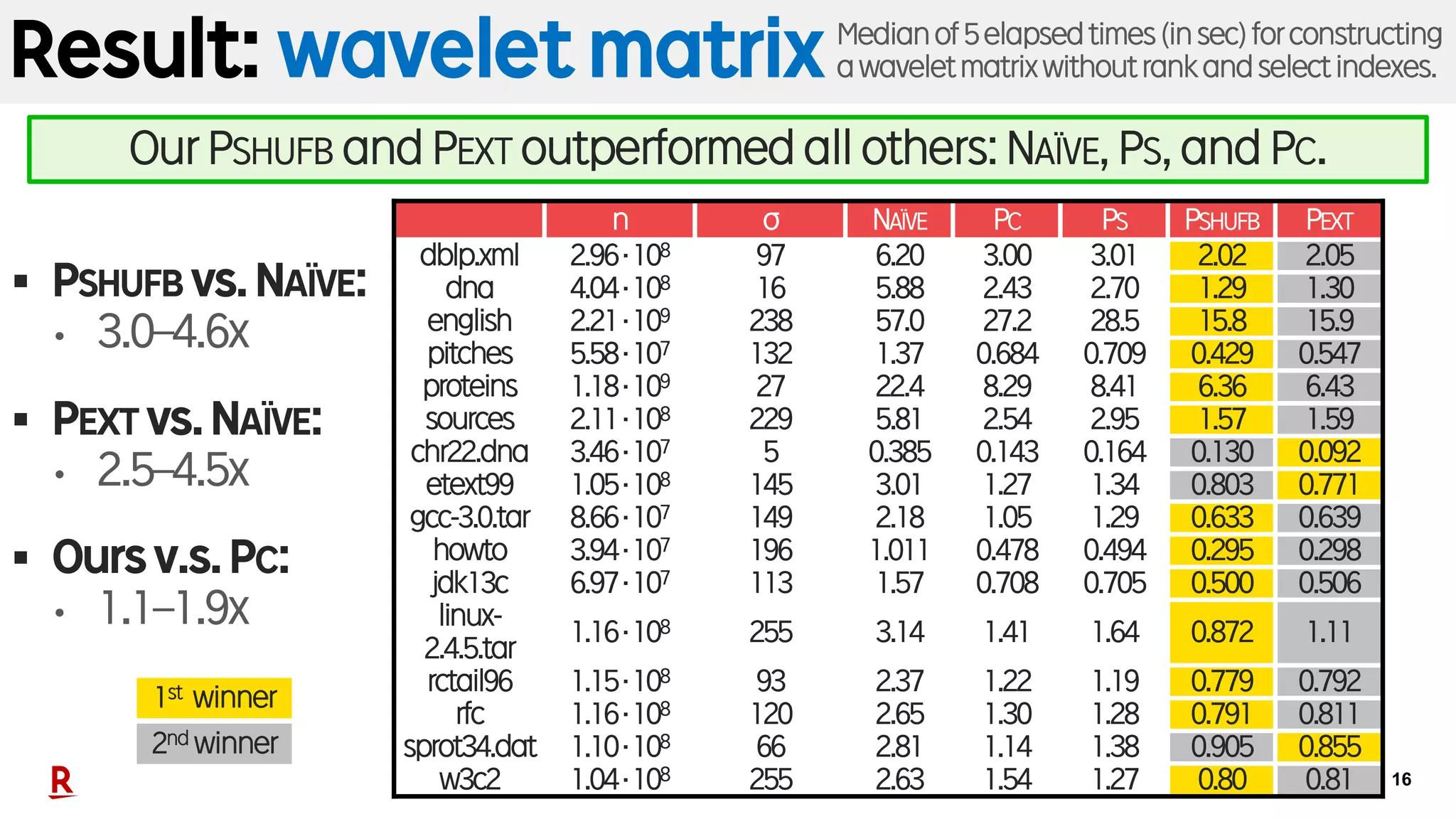
17. 17
Conclusion
§ Practical wavelet tree construction using PEXT/PSHUFB.
• Based on [Munro+, SPIRE’14] and [Babenko+, SODA’15]
§ Experiments on real datasets:
• Wavelet tree: Faster than NAÏVE and competitive w/ SOTA:
prefix sorting (PS) and prefix counting (PC).
• Wavelet matrix: Faster than NAÏVE, PS, and PC.
§ Future work
• Exploit moreparallelismin CPUcoresand/orSIMD registers.