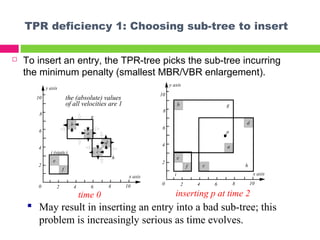
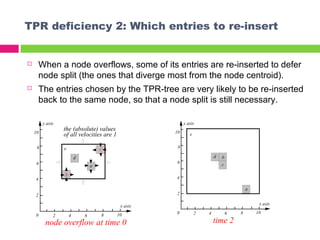
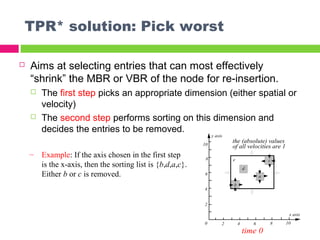
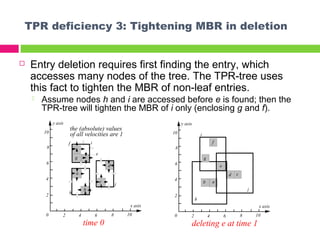
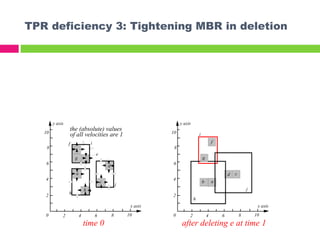
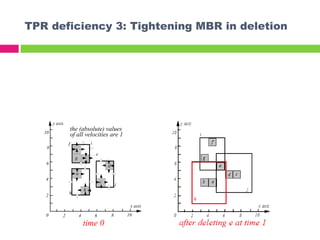
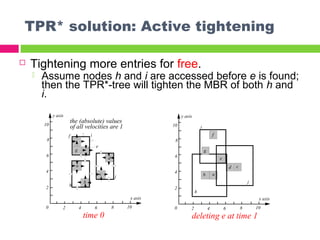
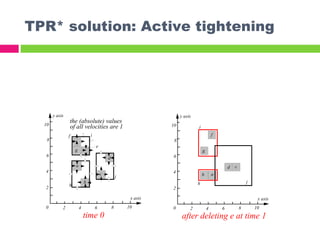
The document describes the TPR*-tree, an optimized index structure for predictive queries on moving objects in spatiotemporal databases. The TPR*-tree improves upon the Time Parameterized R-tree (TPR-tree) by addressing three deficiencies: 1) choosing a better path for insertions, 2) selecting entries that minimize node size for reinsertions, and 3) actively tightening node boundaries during deletions. Experiments showed the TPR*-tree outperformed the TPR-tree in answering predictive queries with fewer disk I/O operations.

1. THE TPR*-TREE: AN
OPTIMIZED
SPATIO-TEMPORAL ACCESS
METHOD FOR PREDICTIVE
QUERIES
Dimitris Papadias
Yufei Tao
Jimeng Sun
VLDB Conference 2003

2. Outline
 Introduction
 The TPR-tree and The TPR*-tree
 Experiments
 Conclusions

3. Introduction
 Spatio-temporal databases
 record moving objects’ geographical locations (sometimes also shapes)
at various timestamps.
 support queries that explore their historical and future (predictive)
behaviors. Applications.
 applications: flight control systems, weather forecast and mobile
computing
 The database stores the motion functions of moving objects.
 For each object o, its motion function gives its location o(t) at any future
time t.
 A predictive window query
 specifies a query region qR and a future time interval qT
 retrieves the set of all objects that will fall in qR during qT.
 our goal: index moving objects so that a predictive window query can
be answered with as few disk I/Os as possible.
 Examples
 Find all airplanes that will be over Florida in the next 10 minutes.
 Report all vessels that will enter the United States in the next hour.

4. Motion Function
 We consider linear motion.
-2
-2
c
2
-2
d
1
-1
a
1
1
1
b
-1
20 4 6 8 10
2
4
6
8
10
x axis
y axis
1
-2
-2
1
at time 0
c
d
a
b
20 4 6 8 10
2
4
6
8
10
x axis
y axis
at time 1
 For each object, the database stores
 Its minimum bounding rectangle (MBR) at the reference time 0
 Its current velocity bounding rectangle (VBR)
 Examples: MBR(a)={2,4,3,4}, VBR(a)={1,1,1,1};
MBR(c)={8,9,3,4}, VBR(c)={-2,0,0,2};
 An update is necessary only when an object’s VBR changes.

5. The Time Parameterized R-Tree (TPR-Tree)
 Extends the R-tree by introducing the velocity bounding
rectangle (VBR) in all entries.
 Queries are compared with conservative MBRs of non-
leaf entries. N1v={-2,1,-2,1} and N2v={-2,0,-1,2}
-2
-2
c
2
-2
d
1
-1
a
1
1 1
1
b
-1
1
-2
-2
-2
2
-1
N
1
N2
20 4 6 8 10
2
4
6
8
10
x axis
y axis
1
-2
-2
1
at time 0
c
d
a
b
N
1
N2
20 4 6 8 10
2
4
6
8
10
x axis
y axis
qR
at time 1

6. TPR*-Tree
 Goal:
 index moving objects so that a predictive window query can be
answered with as few disk I/O as possible.
 A mathematical model that estimates the cost of
answering a predictive window query using TPR-like
structures.
 Number of node accesses.
 Application of the model to derive the optimal
performance.
 The TPR-tree is much worse than the optimal structure.
 Exam the algorithms of the TPR-tree, identify their
deficiencies, and propose new ones.
 The TPR*-tree.

7. TPR*-Tree Insertion
 Choose Path
 Node Insert
 Pick Worst (if overflow)
 Node split

8. TPR deficiency 1: Choosing sub-tree to insert
 To insert an entry, the TPR-tree picks the sub-tree incurring
the minimum penalty (smallest MBR/VBR enlargement).
20 4 6 8 10
2
4
6
8
10
x axis
y axis
c
d
b
a
g
h
the (absolute) values
of all velocities are 1
e
f
i (static)
time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
c
d
a
b g
h
p
e
f
i
inserting p at time 2
 May result in inserting an entry into a bad sub-tree; this
problem is increasingly serious as time evolves.

9. TPR* solution: Choose path
 Aims at finding the best insertion path globally, namely,
among all possible paths.
 Observation: We can find this path by accessing only a few
more nodes (than the TPR-tree algorithm).
20 4 6 8 10
2
4
6
8
10
x axis
y axis
c
d
a
b g
h
p
e
f
i
inserting p at time 2
Maintain a priority queue:
[(g),0], [(h),0], [(i),20]
the path expanded so far
the accumulated penalty so far

10. TPR* solution: Choose path
20 4 6 8 10
2
4
6
8
10
x axis
y axis
c
d
a
b g
h
p
e
f
i
inserting p at time 2
Visit node g:
[(h),0], [(a,g),3], [(i),20],
[(b,g),32]
complete paths already
although nodes a and b are
not visited

11. TPR* solution: Choose path
20 4 6 8 10
2
4
6
8
10
x axis
y axis
c
d
a
b g
h
p
e
f
i
inserting p at time 2
Visit node h:
[(a,g),3], [(d,h),9],
[(c,h),17], [(i),20],
[(b,g),32]
The algorithm stops now.

12. TPR deficiency 2: Which entries to re-insert
 When a node overflows, some of its entries are re-inserted to defer
node split (the ones that diverge most from the node centroid).
 The entries chosen by the TPR-tree are very likely to be re-inserted
back to the same node, so that a node split is still necessary.
20 4 6 8 10
2
4
6
8
10
x axis
y axis
b
c
a
e
the (absolute) values
of all velocities are 1
d
node overflow at time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
b
c
a
e
d
time 2

13. TPR* solution: Pick worst
 Aims at selecting entries that can most effectively
“shrink” the MBR or VBR of the node for re-insertion.
 The first step picks an appropriate dimension (either spatial or
velocity)
 The second step performs sorting on this dimension and
decides the entries to be removed.
20 4 6 8 10
2
4
6
8
10
x axis
y axis
b
c
a
e
the (absolute) values
of all velocities are 1
d
time 0
– Example: If the axis chosen in the first step
is the x-axis, then the sorting list is {b,d,a,c}.
Either b or c is removed.

14. TPR* solution: Node Split
 Computes the overall perimeter for each
dimension
 Select the split axis as the smallest overall
perimeter
 Perimeter defined as the perimeter of the
sweeping region of the corresponding
transformed rectangle
 Perimeter computation is very efficient
 The number of vertices of a sweeping region is small

15. TPR deficiency 3: Tightening MBR in deletion
 Entry deletion requires first finding the entry, which
accesses many nodes of the tree. The TPR-tree uses
this fact to tighten the MBR of non-leaf entries.
 Assume nodes h and i are accessed before e is found; then the
TPR-tree will tighten the MBR of i only (enclosing g and f).
20 4 6 8 10
2
4
6
8
10
x axis
y axis
the (absolute) values
of all velocities are 1
f
e
g
a
b
d
c
i
j
h
time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
f
e
g
b a
d c
i
j
h
deleting e at time 1

16. TPR deficiency 3: Tightening MBR in deletion
20 4 6 8 10
2
4
6
8
10
x axis
y axis
the (absolute) values
of all velocities are 1
f
e
g
a
b
d
c
i
j
h
time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
f
g
b a
d c
i
j
h
after deleting e at time 1

17. TPR deficiency 3: Tightening MBR in deletion
20 4 6 8 10
2
4
6
8
10
x axis
y axis
the (absolute) values
of all velocities are 1
f
e
g
a
b
d
c
i
j
h
time 0

18. TPR* solution: Active tightening
 Tightening more entries for free.
 Assume nodes h and i are accessed before e is found;
then the TPR*-tree will tighten the MBR of both h and
i.
20 4 6 8 10
2
4
6
8
10
x axis
y axis
the (absolute) values
of all velocities are 1
f
e
g
a
b
d
c
i
j
h
time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
f
e
g
b a
d c
i
j
h
deleting e at time 1

19. TPR* solution: Active tightening
20 4 6 8 10
2
4
6
8
10
x axis
y axis
the (absolute) values
of all velocities are 1
f
e
g
a
b
d
c
i
j
h
time 0
20 4 6 8 10
2
4
6
8
10
x axis
y axis
f
g
b a
d c
i
jh
after deleting e at time 1

20. TPR* solution: Active tightening
 Another example: Assume the shaded nodes are accessed to
find e.
 The active tightening can tighten the MBR of n5, n6, n3, and n4.
 But not n1 and n2.
n1 n2
n5 n6
n3 n4
root
...
...e
to be written
back to disk
N1 N2 N3 N4
N5 N6

21. Challenge of Migration
 3 Operating Systems:
 Microsoft Windows
 Sun Solaris
 Redhat Fedora Core 1
 2 Compilers: CL, GCC (2.9.5, 3.3.2)
 Difference of Code Conversion
 How close the compilers to the standard?
 Compatibility of Library

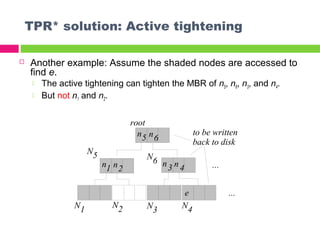
22. Experiments: Settings (query and tree)
 Dataset
 50,000 sampled objects’ MBRs are taken from a real spatial dataset NJ
[Tiger]
 each object is associated with a VBR such that on each dimension
 The velocity extent is zero (i.e., the object does not change
spatial extents during its movement)
 the velocity value distribution is randomed in range [0,8]
 the velocity can be positive or negative with equal probability.
 We compare TPR*- with TPR-trees.
 Disk page size=1k bytes (node capacity=27 for both trees).
 For each object update, perform a deletion followed by an insertion on each
tree.
 Each predictive query is a moving rectangle, and has these
parameters:
 qRlen: The length of the query’s MBR
 qVlen: The length of the query’s VBR
 qTlen: The number of timestamps covered.

23. Conclusions
 The TPR-tree combines the idea of conservative
MBR directly with the tree construction
algorithms of R*-trees.
 The TPR*-tree improves it by designing
algorithms that take into account the special
features for moving objects.
 Cost model for performance analysis
 The optimal performance of a “hypothetically best
structure”
 Reduce disk I/Os for predictive queries