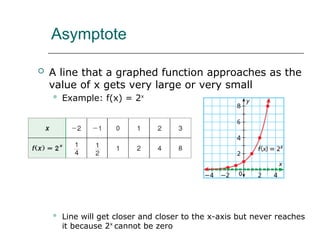
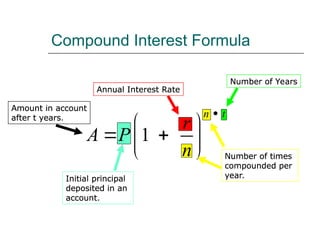
The document discusses exponential functions, specifically focusing on modeling real-life situations involving growth and decay. It includes explanations of graphing these functions, examples of interest calculations, and practical applications such as the growth of cell phone subscribers and the depreciation of a car's value. Additionally, the document provides formulas for compound interest and examples of calculating account balances based on different compounding frequencies.

1. Exponential Functions, Growth
and Decay
Goal: Graph exponential growth and
decay functions and use exponential
growth and decay functions to model
real-life situations.

2. Exponential Function
 A function in the form:
Base is Constant
Exponent is the Independent
Variable

3. Asymptote
 A line that a graphed function approaches as the
value of x gets very large or very small
 Example: f(x) = 2x
 Line will get closer and closer to the x-axis but never reaches
it because 2x
cannot be zero

4. Graphing Exponential Functions
 To graph an exponential function of
the form y = abx-h
+k, sketch graph of
abx
, then translate the graph
horizontally by h units and veritcally
by k units.

5. If you invested $200.00 in an account that paid
simple interest, find how long you’d need to leave it
in at 4% interest to make $10.00
In 1985, there were 285 cell phone subscribers in the
small town of Centerville. The number of subscribers
increased by 75% per year after 1985. How many
cell phone subscribers were in Centerville in 1994?
Bacteria can multiply at an alarming rate when each
bacteria splits into two new cells, thus doubling. For
example, if we start with only one bacteria which can
double every hour, by the end of one day we will
have over 16 million bacteria.
Graphing Exponential Functions
How does this apply to real life situations?

6. Percent Increase and Decrease
You can model growth or decay by a
constant percent increase or percent
decrease with the formula:
A(t) = a (1 + r)t
1+r is growth factor
1-r is decay factor
Final Amount Rate of Increase
Initial Amount
Number of Time Periods

7. 1. In January, 1993 , there were about 1,313,000
Internet hosts. During the next 5 years the number
of hosts increased by about 100% per year.
Step 1: Write a function to model the number h (in millions) of
hosts t years after 1993. About how many hosts were there in
1996?
Step 2: Graph the function.
Step 3: Use the graph to estimate the year when there were 30
million hosts.

8. 2. You buy a new car for $24,000. The value y of the
car decreases by 16% each year.
Step 1: Write a function to model the value of the car. Use the
model to estimate the value after 2 years.
Step 2: Graph the function.
Step 3: Use the graph to estimate when the value of the car will
have a value of $12,000.

9. Compound Interest Formula
1
n t
r
A P
n

 
 
 
 
Initial principal
deposited in an
account.
Annual Interest Rate
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
1
n t
r
A P
n

 
 
 
 
Initial principal
deposited in an
account.
Annual Interest Rate
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Amount in account
after t years.
Number of Years
Annual Interest Rate
Amount in account
after t years.
Number of times
compounded per
year.
Number of Years
Annual Interest Rate
Amount in account
after t years.
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Annual Interest Rate
Amount in account
after t years.
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Annual Interest Rate
Amount in account
after t years.
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Annual Interest Rate
Amount in account
after t years.
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.
Annual Interest Rate
Initial principal
deposited in an
account.
Number of times
compounded per
year.
Number of Years
Amount in account
after t years.

10. 1. You deposit $1,000 in an account that pays 8% annual
interest. Find the balance after 1 year if the interest is
compounded with the given frequency.
a. Annually
a. Quarterly
a. Daily

11. 2. You deposit $1,600 in a band account. Find the
balance after 3 years if the account pays 2.5%
annual interest compounded monthly.
3. What if the account paid 1.75% annual interest
compounded quarterly?