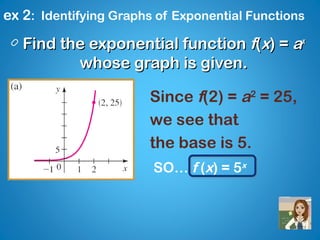
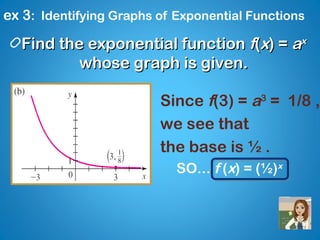
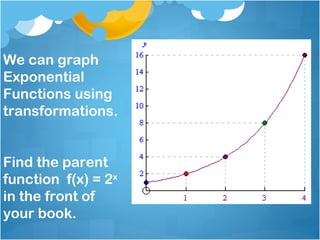
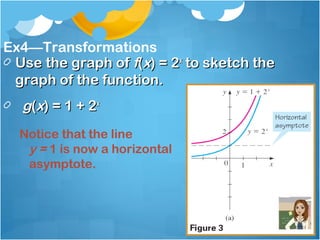
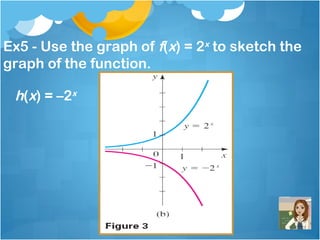
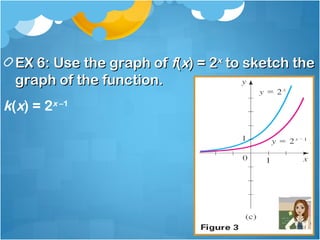
This document provides information and examples about exponential functions. It defines the exponential function f(x) = ax, where a is the base and a > 0, a ≠ 1. It gives examples of evaluating exponential functions for different bases and inputs. It discusses the domain and range of exponential functions. It provides examples of identifying the base of an exponential function given its graph. It discusses how to graph exponential functions using transformations of the parent function f(x) = 2x.

1. l Note s 4 -1
PreC a IICK
K
ctions
L C !!!
C L !!!
ial Fun
C E
ME
one nt
M
Exp

2. GET YOUR CALCULATOR!!

3. Definition: Exponential Function
The exponential function with base a
is defined by:
f(x) = ax
where a > 0 and a ≠ 1.

4. Ex 1—Evaluating Exponential Functions
Let f(x) = 3x and evaluate the following:
(a) f(2) = 32 = 3 ^ 2 ENTER = 9
(b) f(–⅔) = 3-⅔ =3 ^((–) 2÷3 ) ENTER
≈ 0.4807
(c) f(π) = 3π = 3^π ENTER ≈ 31.544
(d) f( √2 ) = 3√2 = 3^√ 2) ENTER ≈ 4.7288
Hint: you will need a calculator!!

5. Graphs of Exponential Functions
F(x) = ax
Domain: All real numbers
Range: (0, ∞)

6. ex 2: Identifying Graphs of Exponential Functions
Find the exponential function f(x) = ax
whose graph is given.
Since f(2) = a2 = 25,
we see that
the base is 5.
SO… f (x) = 5x

7. ex 3: Identifying Graphs of Exponential Functions
Find the exponential function f(x) = ax
whose graph is given.
Since f(3) = a3 = 1/8 ,
we see that
the base is ½ .
SO... f (x) = (½)x

8. reak ! !!!
Brain B

9. Speaking of Infinity…
Make an infinity symbol with your right hand out in front of
you. and stop your finger on the far right side of the
infinity sign.
Lift your left hand to be at the far left side of the infinity
sign. Now move your hands at the same time and the
same pace in the same direction to continue your infinity
sign. Your hands should cross the middle at the same
time.
This one seems easy at first. Then you try to do it when
your hands are doing the infinity signs in different
directions. You should look like a choir director if you are
doing it correctly. 

10. We can graph
Exponential
Functions using
transformations.
Find the parent
function f(x) = 2x
in the front of
your book.

11. Ex4—Transformations
Use the graph of f(x) = 2x to sketch the
graph of the function.
g(x) = 1 + 2x
Notice that the line
y = 1 is now a horizontal
asymptote.

12. Ex5 - Use the graph of f(x) = 2x to sketch the
graph of the function.
h(x) = –2x

13. EX 6: Use the graph of f(x) = 2x to sketch the
graph of the function.
k(x) = 2x –1

14. You have finished your Homework!!
Great job!
Now go get a cookie for yourself!
;)