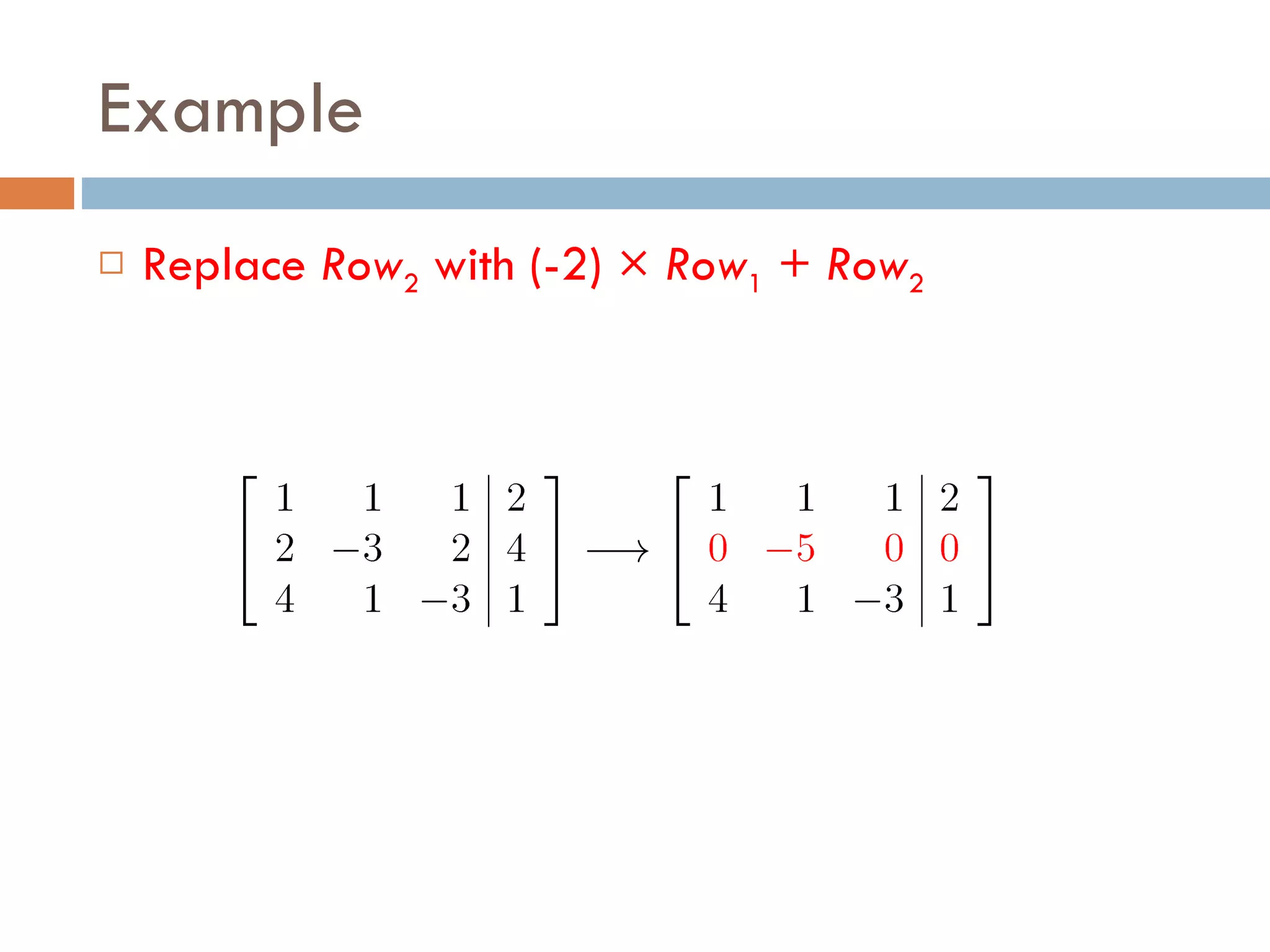
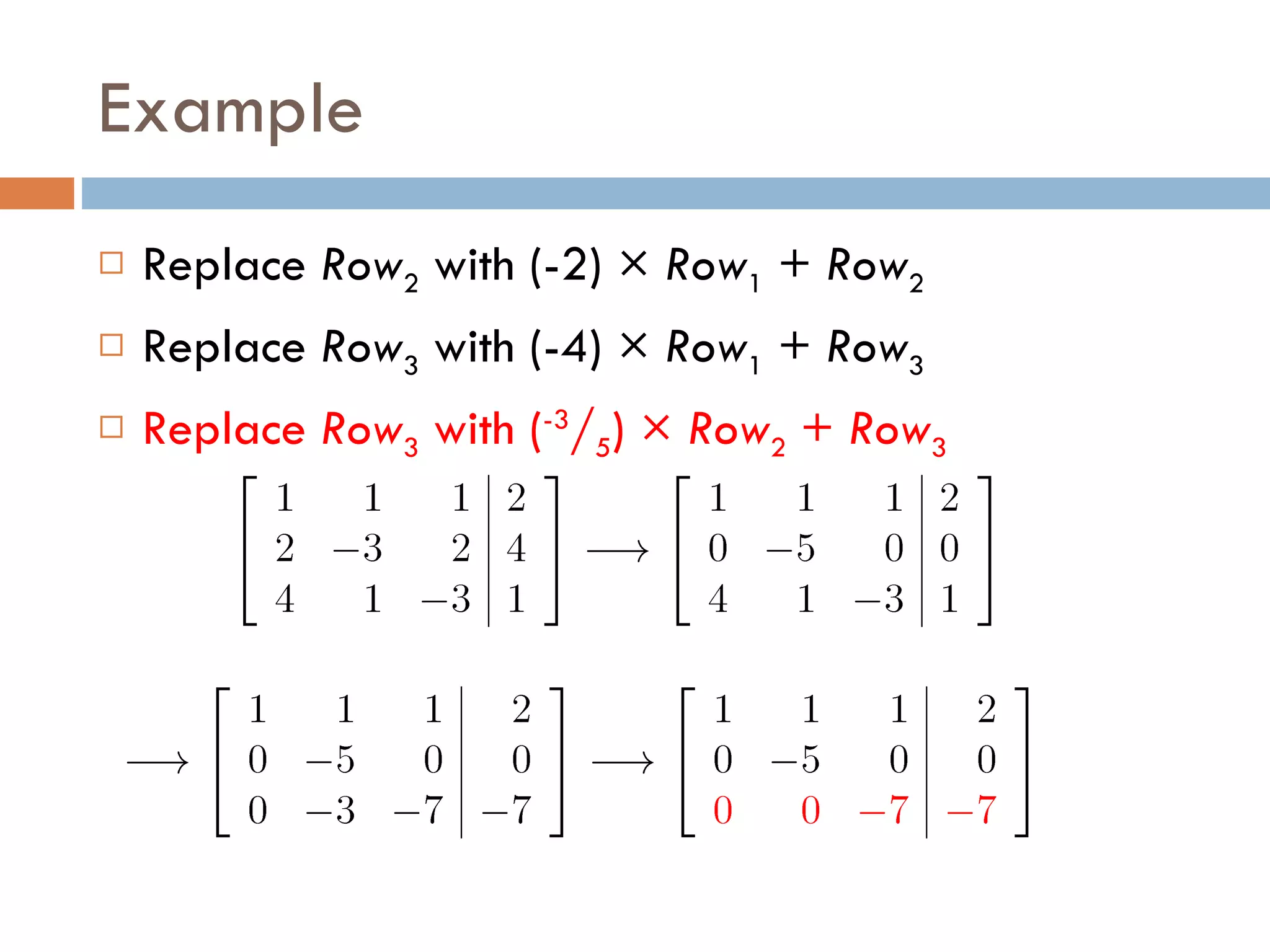
Gaussian elimination is a method for solving systems of linear equations by transforming the augmented matrix of coefficients into row-echelon form using elementary row operations. The document provides an example of using Gaussian elimination to solve a system of 3 equations by first writing the augmented matrix and then performing a sequence of row operations to obtain the row-echelon form from which the solution can be extracted with back substitution.

1. Gaussian Elimination Image from WikiMedia Commons created in LightWave by stib http://commons.wikimedia.org/wiki/File:Secretsharing-3-point.png

2. Example Solve the system of linear equations using Gaussian elimination.

3. Example First, we write the augmented matrix. System of equations: Augmented matrix:

4. Example Now we perform a sequence of elementary row operations to obtain a row-equivalent matrix in row-echelon form.

5. Example

6. Example Replace Row 2 with (-2) × Row 1 + Row 2

7. Example Replace Row 2 with (-2) × Row 1 + Row 2 Replace Row 3 with (-4) × Row 1 + Row 3

8. Example Replace Row 2 with (-2) × Row 1 + Row 2 Replace Row 3 with (-4) × Row 1 + Row 3 Replace Row 3 with ( -3 / 5 ) × Row 2 + Row 3

9. Example The augmented matrix is now in row-echelon form.

10. Example The associated system can be solved by backward substitution. The solution is (1, 0, 1). System of equations: Augmented matrix: