기초적인 Linear Algebra 와 Matrix Calculus 부터 Back-propagation 까지 유도하는 슬라이드입니다. 본 슬라이드에서는 다차원 공간에서의 기초 미적분학 공식으로부터 Back-propagation 까지 유도합니다.

1. Math Tutorial II
Linear Algebra & Matrix Calculus
임성빈

2. Matrix Calculus and Applications

3. 지난시간엔기초적인선형대수학을배웠습니다
이번엔이를활용한Matrix Calculus 를배우겠습니다
후반부엔이를가지고 어떻게 응용하는지살펴봅시다
Linear Regression Analysis
Back propagation in DL

4. 태초에모든게 여기서부터시작했죠..
f : R → R
f = =
미분은아래공식으로도계산할수있습니다
f = =
′
dx
df
h→0
lim
h
f(x + h) − f(x)
′
h→0
lim
h
f(x) − f(x − h)
h→0
lim
2h
f(x + h) − f(x − h)

5. 미분의가장중요한성질(Very Important Property)
Linearity
(αf + βg) = αf + βg
Product rule
(fg) = f g + g f
Chain rule
(f(g)) = g f (g)
′ ′ ′
′ ′ ′
′ ′ ′

6. 이를벡터와행렬로확장해보자...!

7. 독립변수가 벡터인경우..
f : R → R 이면편미분(partial derivative) 을정의합니다
∂ f = =
그리고 편미분을모은벡터를gradient 벡터라부릅니다
∇f = (∂ f, ⋯ , ∂ f)
Note : gradient 는(d, 1)‑열벡터입니다
d
xi
∂xi
∂f
h→0
lim
h
f(x + he ) − f(x)i
x1 xd

8. VIP for multivariable function
Linearity
∇(f + g) = ∇f + ∇g
Product rule
∇(fg) = (∇f)g + (∇g)f
Chain rule (f : R → R)
∇(f(g)) = ∇gf (g) = (∂ gf (g), … , ∂ gf (g))′
x1
′
xd
′

9. 벡터함수인경우..
F : R →R i.e.
F(x) = (f (x), … , f (x))
∇F(x) = (f (x), … , f (x))
Note : ∇F 는(1, d)‑행벡터입니다.
d
1 d
1
′
d
′

10. VIP for vector‑valued function
Linearity
∇(F + G) = ∇F + ∇G
Product rule : F G ∈ R
∇(F G) = (∇F)G + (∇G)F
Chain rule (f : R → R)
∇(f(G)(x)) = (∇G(x))(∇f(G(x))) = g (x) (G(x))
T
T
d
i=1
∑
d
i
′
∂yi
∂f

11. ∇(f(G)) = = = g (G)
dx
dz
i=1
∑
d
dx
dyi
∂yi
∂z
i=1
∑
d
i
′
∂yi
∂f

12. Vector‑valued multivariable 함수인경우..
F : R →R i.e.
F(x) = (f (x), … , f (x))
∇F = (∇f , … , ∇f ) =
Note : ∇F 는(n, m)‑행렬이다!
n m
1 m
1 m
⎣
⎡∂ fx1 1
⋮
∂ fxn 1
∂ fx1 2
⋮
∂ fxn 2
⋯
⋮
⋯
∂ fx1 m
⋮
∂ fxn m
⎦
⎤

13. Linearity
∇(F + G) = ∇F + ∇G
Product rule : F G ∈ R
∇(F G) = (∇F)G + (∇G)F
Chain rule : G :R →R , F :R →R
∇(F(G)(x)) = (∇G(x))(∇F(G(x)))
T
T
n k k m

14. Summary
선형대수는그저차원맞춤법!
Definition 은이해가 아니라암기!

15. 변수가 행렬이면요?
(임모씨) : 좀만기다려달라아직은때가 아니다..

16. Case 1: Linear Regression Analysis

17. 통계학과에서선형대수를배우는첫번째이유
그 때는외우면된다고 생각했지...

18. Variables
Input : X ∈R
Unknown parameters : β ∈R
Model : = Xβ ∈R
Goal : Solve
∥ − Y∥ = ∥Xβ − Y∥
위방법론을최소제곱법(Least square method) 이라부릅니다
n×k
k
Y^ n
β
min Y^ 2
β
min 2

19. 가장간단한예
y = βx + ϵ , i ∈ {1, … , n}
이경우오차들의제곱의합은..
∥y − ∥ = (y − βx )
i i i
y^ 2
2
i=1
∑
n
i i
2

20. 최소값을구하려면미분해야합니다!
그러므로
y x = β x
이를다시쓰면!
x y = βx x
∥y − ∥
∂β
∂
y^ 2
2
= 2 (y − βx )(−x ) = 0
i=1
∑
n
i i i
i=1
∑
n
i i
i=1
∑
n
i
2
T T

21. ∴ β = (x x) x y
이걸 다중회귀 문제로바꿔보자...!
y = x β + ϵ
달리쓰면...
Y = Xβ + ϵ
T −1 T
i
j=1
∑
k
ij j i

22. 일단풀어서써봅니다...
∥Xβ − Y∥2
2
= (Xβ − Y) (Xβ − Y)T
= β X Xβ −Y Xβ − β X Y +Y YT T T T T T

23. 최소값을구하려면또미분해야합니다!
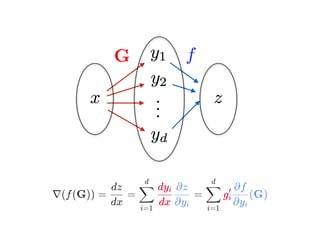
∇ ∥Xβ − Y∥β 2
2
= ∇ (Xβ) Xβ − (X Y) β − β X Y +Y Yβ ( T T T T T T
)
= ∇ Xβ Xβ + ∇ Xβ Xβ − (X Y) −X Yβ [ ] β [ ] T T
= 2X Xβ − 2X Y = 0T T

24. ∴ X Xβ =X Y
만약k ≤ n 이고 다중공선성이없다면rank(X X) = k 이므로X X
는역행렬이존재한다:
∴ β = (X X) X Y
참고로아까전엔...
β = (x x) x y
... 선형대수는그저차원맞춤법일뿐!
T T
T T
∗ T −1 T
∗ T −1 T

25. 몇가지쫌센가정이충족된다면 는unbiased, consistent, efficient 한
최적선형추정량(Optimal linear estimator) 이됩니다
= E[Y∣X, β]
Y^
Y^

26. Case 2: Back Propagation in DL
직접손으로써보면서연습합시다

27. Variables
Input : x =z
Output in Hidden Layer ℓ : z = f (W z )
z = f W z , i ∈ {1, … , d }
Output : = f (W z )
(0)
(ℓ)
(ℓ)
(ℓ) (ℓ−1)
i
(ℓ) (ℓ)
(
j=1
∑
dℓ
ij
(ℓ)
j
(ℓ−1)
) ℓ
y^ (L)
(L) (L−1)

28. Loss Function
Mean‑Square Error
L( ∣y) = ∥y − ∥
Cross‑Entropy
L( ∣y) = − [y ⋅ log + (1 − y) ⋅ log(1 − )]
y^
2
1
p∈Batch
∑ p y^p 2
2
y^
dL
1
p∈Batch
∑ y^ y^

29. Gradient Descdent Optimization Algorythm
W ← W − α
또는(i, j 들을더선호하신다면.. )
W = W − α
(ℓ) (ℓ)
∂W(ℓ)
∂L
ij
(ℓ,n)
ij
(ℓ,n−1)
W
∂W ij
(ℓ,n−1)
∂L

30. 일단제일쉽게...
z1
z2
zℓ
zL
= f(W x)1
= f(W z )2 1
⋮
= f(W z )ℓ ℓ−1
⋮
= f(W z )L L−1

31. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1

32. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1
= δ WL L
∂Wℓ
∂zL−1

33. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1
= δ WL L
∂Wℓ
∂zL−1
= δ W f (W z )WL L
′
L−1 L−2 L−1
∂Wℓ
∂zL−2

34. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1
= δ WL L
∂Wℓ
∂zL−1
= δ W f (W z )WL L
′
L−1 L−2 L−1
∂Wℓ
∂zL−2
= δ WL−1 L−1
∂Wℓ
∂zL−2

35. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1
= δ WL L
∂Wℓ
∂zL−1
= δ W f (W z )WL L
′
L−1 L−2 L−1
∂Wℓ
∂zL−2
= δ WL−1 L−1
∂Wℓ
∂zL−2
= ⋯
= δ Wℓ+1 ℓ+1
∂Wℓ
∂zℓ
= δ W f (W z )zℓ+1 ℓ+1
′
ℓ ℓ−1 ℓ−1

36. =L (z )
∂Wℓ
∂L ′
L
∂Wℓ
∂zL
=L (z )f (W z )W′
L
′
L L−1 L
∂Wℓ
∂zL−1
= δ WL L
∂Wℓ
∂zL−1
= δ W f (W z )WL L
′
L−1 L−2 L−1
∂Wℓ
∂zL−2
= δ WL−1 L−1
∂Wℓ
∂zL−2
= ⋯
= δ Wℓ+1 ℓ+1
∂Wℓ
∂zℓ
= δ W f (W z )z = δ zℓ+1 ℓ+1
′
ℓ ℓ−1 ℓ−1 ℓ ℓ−1

37. Derivation of Back‑propagation
=
Note : Dimension check : (d , d ) ‑ 행렬
∂W(ℓ)
∂L( )y^
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
∂W11
(ℓ)
∂L( )y^
⋮
∂Wd 1ℓ
(ℓ)
∂L( )y^
∂W12
(ℓ)
∂L( )y^
⋮
∂Wd 2ℓ
(ℓ)
∂L( )y^
⋯
⋮
⋯
∂W1dℓ−1
(ℓ)
∂L( )y^
⋮
∂Wd dℓ ℓ−1
(ℓ)
∂L( )y^
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤
ℓ ℓ−1

38. = ∇ L
(d , d ) ≠ (d , d , d ) × (d , 1)
어라...? 계산이꼬인다...
∂Wℓ
∂L( )y^ ?
∂Wℓ
∂y^
y^
ℓ ℓ−1 ℓ ℓ−1 L L

39. Back‑propagation 은벡터화연산자가 필요합니다

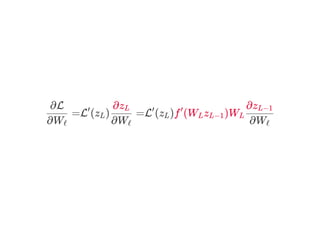
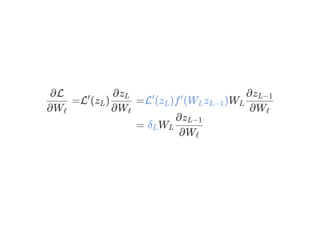
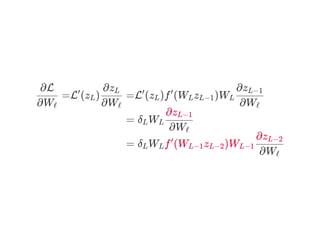
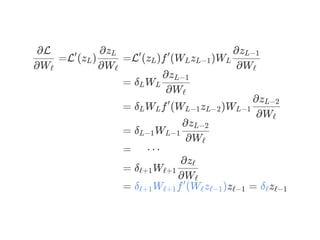
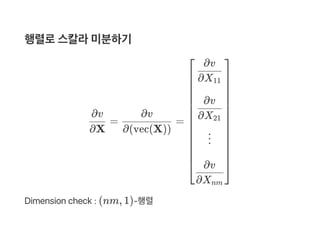
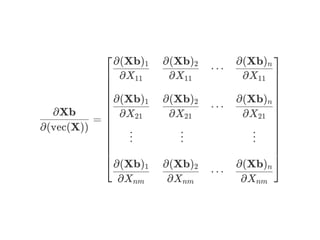
40. 벡터화연산자
X : (n, m)‑행렬
vec(X) =
X = np.array([[x11,..,x1m],..[xn1,..xnm]]) # (n,m)-행렬
vec_X = np.reshape(X,(nm,1),'F') # (nm,1)-행렬
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡ X11
X21
⋮
Xn1
X12
X22
⋮
Xnm
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

41. vec 은NumPy 에서지원안합니다...
def vec(matrix):
dim = np.prod(matrix.shape)
vec_matrix = np.reshape(matrix,(dim,1),'F')
return(vec_matrix)

42. 행렬로스칼라미분하기
= =
Dimension check : (nm, 1)‑행렬
∂X
∂v
∂(vec(X))
∂v
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
∂X11
∂v
∂X21
∂v
⋮
∂Xnm
∂v
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

43. 행렬로벡터미분하기
= =
Dimension check : (nm, d)‑행렬
∂X
∂v
∂(vec(X))
∂v
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
∂X11
∂v1
∂X21
∂v1
⋮
∂Xnm
∂v1
∂X11
∂v2
∂X21
∂v2
⋮
∂Xnm
∂v2
⋯
⋯
⋱
⋯
∂X11
∂vd
∂X21
∂vd
⋮
∂Xnm
∂vd
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

44. 예제) 다음을계산하시오
X : (n, m)‑행렬, b : (m, 1)‑벡터
= ?
∂X
∂Xb

45. (Solution)
=
Dimension check : (nm, n) ‑ 행렬
∂X
∂Xb
∂(vec(X))
∂Xb

46. =
∂(vec(X))
∂Xb
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
∂X11
∂(Xb)1
∂X21
∂(Xb)1
⋮
∂Xnm
∂(Xb)1
∂X11
∂(Xb)2
∂X21
∂(Xb)2
⋮
∂Xnm
∂(Xb)2
⋯
⋯
⋯
∂X11
∂(Xb)n
∂X21
∂(Xb)n
⋮
∂Xnm
∂(Xb)n
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

47. = =
∂(vec(X))
∂Xb
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡b1
0
⋮
0
−
⋮
−
bm
0
⋮
0
0
b1
⋮
0
−
⋮
−
0
bm
⋮
0
⋯
⋯
⋮
0
−
⋮
−
⋯
⋯
⋮
0
0
0
⋮
b1
−
⋮
−
0
0
⋮
bm
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡b I1 n
b I2 n
⋮
b Im n
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

48. Kronecker product
A : (n, m)‑행렬, B : (p, q)‑행렬
A ⊗ B =
A ⊗ B 는(np, mq)‑행렬이다
⎣
⎢
⎢
⎡a B11
a B21
⋮
a Bn1
a B12
a B22
⋮
a Bn2
⋯
⋯
⋱
⋯
a B1m
a B2m
⋮
a Bnm
⎦
⎥
⎥
⎤

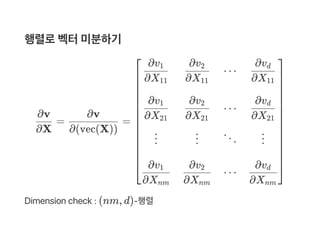
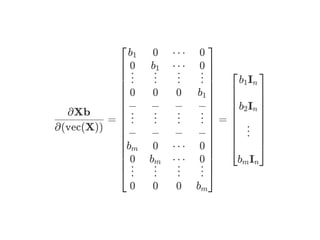
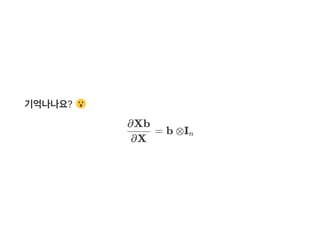
49. = b ⊗I
I = np.eye(n) # (n,n)-Identity matrix
b = np.array([[b1],..,[bm]]) # (m,1)-Column vector
np.kron(b,I) # (mn,n)-matrix : Kronecker product
∂X
∂(Xb)
n

50. (재도전) Derivation of Back‑propagation Algorythm
:= = ∇ L
(d d , 1) = (d d , d ) × (d , 1)
∂Wℓ
∂L( )y^
∂(vec(W ))ℓ
∂L( )y^
∂(vec(W ))ℓ
∂y^
y^
ℓ ℓ−1 ℓ ℓ−1 L L

51. =
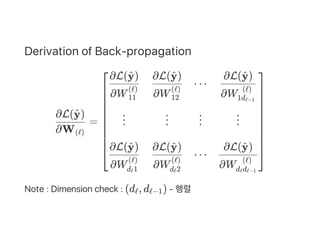
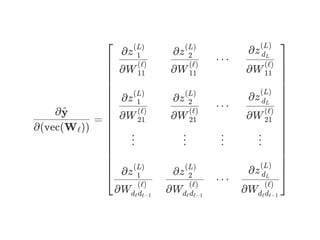
∂(vec(W ))ℓ
∂y^
[
∂(vec(W ))ℓ
∂z 1
(L)
⋯
∂(vec(W ))ℓ
∂z dL
(L)
]

52. =
∂(vec(W ))ℓ
∂y^
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
∂W11
(ℓ)
∂z 1
(L)
∂W21
(ℓ)
∂z 1
(L)
⋮
∂Wd dℓ ℓ−1
(ℓ)
∂z 1
(L)
∂W11
(ℓ)
∂z 2
(L)
∂W21
(ℓ)
∂z 2
(L)
⋮
∂Wd dℓ ℓ−1
(ℓ)
∂z 2
(L)
⋯
⋯
⋮
⋯
∂W11
(ℓ)
∂z dL
(L)
∂W21
(ℓ)
∂z dL
(L)
⋮
∂Wd dℓ ℓ−1
(ℓ)
∂z dL
(L)
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

53. 여기서∇f 는다음과 같은(d , d )‑대각행렬입니다
∇f =
=
∂Wℓ
∂y^
∂(vec(W ))ℓ
∂f (W z )L L (L−1)
= ∇f
∂(vec(W) )ℓ
∂(W z )L (L−1)
L
L L L
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
f W z′
(
k=1
∑
dL
1k
(L)
k
(L−1)
)
⋱
f W z′
(
k=1
∑
dL
d kL
(L)
k
(L−1)
)
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤

54. ∇f 와∇ L 이곱해지면다음과 같은(d , 1) 행렬이나온다
= diag(∇f ) ⊙ ∇ L
L y L
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎡
f W z′
(
k=1
∑
dL
1k
(L)
k
(L−1)
)
∂y1
∂L
⋮
f W z′
(
k=1
∑
dL
1k
(L)
k
(L−1)
)
∂ydL
∂L
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎤
L y

55. 표기를간단히하기 위해delta 기호를씁시다
δ = diag(∇f ) ⊙ ∇ LL L y

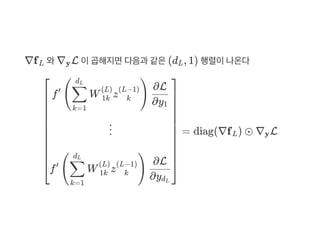
56. 그러므로... (만약ℓ = L 인경우)
Dimension check :
(d d , 1) = (d d , d ) × (d , 1)
∂WL
∂L( )y^
= diag(∇f ) ⊙ ∇ L
∂(vec(W ))L
∂(W z )L (L−1)
[ L y ]
=z ⊗I δ(L−1) dL L
L L−1 L L−1 L−1 L

57. 그러므로... (만약ℓ ≠ L 인경우)
Dimension check :
(d d , d ) × (d , d ) × (d , 1)
∂Wℓ
∂L( )y^
= diag(∇f ) ⊙ ∇ L
∂(vec(W ))ℓ
∂(W z )L (L−1)
[ L y ]
= W δ
∂(vec(W ))ℓ
∂z(L−1)
L
T
L
ℓ ℓ−1 L−1 L−1 L L

58. 한번더?

59. 뭐한번해보죠...
∂Wℓ
∂L( )y^
= W δ
∂(vec(W ))ℓ
∂z(L−1)
L
T
L
= W δ
∂(vec(W ))ℓ
∂f (W z )L−1 L−1 (L−2)
L
T
L
= diag(∇f ) ⊙W δ
∂(vec(W ))ℓ
∂(W z )L−1 (L−2)
[ L−1 L
T
L]
= W δ
∂(vec(W ))ℓ
∂z(L−2)
L−1
T
L−1

60. 계속하세요
=
∂Wℓ
∂L( )y^
W δ
∂(vec(W ))ℓ
∂z(L−2)
L−1
T
L−1
= W δ
∂(vec(W ))ℓ
∂f (W z )L−2 L−2 (L−3)
L−1
T
L−1
= diag(∇f ) ⊙W δ
∂(vec(W ))ℓ
∂(W z )L−2 (L−3)
[ L−2 L−1
T
L−1]
= W δ
∂(vec(W ))ℓ
∂z(L−3)
L−2
T
L−2

61. 어라패턴이있네요?
= W δ
∂Wℓ
∂L( )y^
∂(vec(W ))ℓ
∂z(L−3)
L−2
T
L−2

62. = ⋯
∂Wℓ
∂L( )y^
= W δ
∂(vec(W ))ℓ
∂zℓ
ℓ+1
T
ℓ+1
= W δ
∂(vec(W ))ℓ
∂f (W z )ℓ ℓ (ℓ−1)
ℓ+1
T
ℓ+1
= diag(∇f ) ⊙W δ
∂(vec(W ))ℓ
∂(W z )ℓ (ℓ−1)
[ ℓ ℓ+1
T
ℓ+1]
= δ
∂(vec(W ))ℓ
∂(W z )ℓ (ℓ−1)
ℓ

63. 기억나나요?
= b ⊗I
∂X
∂Xb
n

64. Dimension check :
= δ =z ⊗I δ
∂Wℓ
∂L( )y^
∂(vec(W ))ℓ
∂(W z )ℓ (ℓ−1)
ℓ (ℓ−1) dℓ ℓ
(d d , 1)ℓ ℓ−1 = (d , 1) ⊗ (d , d ) × (d , 1)ℓ−1 ℓ ℓ ℓ
= (d d , d ) × (d , 1)ℓ ℓ−1 ℓ ℓ

65. 물론이벡터는행렬로도로바꿀수있습니다
= δ z
Dimension check :
∂Wℓ
∂L( )y^
ℓ (ℓ−1)
T
(d , d )ℓ ℓ−1 = (d , 1) × (1, d )ℓ ℓ−1

66. Back‑propagation via Matrix Calculus
= ∇f W ∇f ∇ L( )z
Dimension check :
∂Wℓ
∂L( )y^
ℓ
⎝
⎛
j=ℓ+1
∏
dL
j
T
j
⎠
⎞
y y^ (ℓ−1)
T
(d , d ) = (d , d ) × (d , d ) × (d , d )ℓ ℓ−1 ℓ ℓ
⎝
⎛
j=ℓ+1
∏
dL
j−1 j j j
⎠
⎞
×(d , 1) × (1, d )L ℓ−1

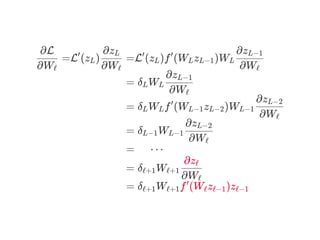
67. Back‑propagation Algorythm
위를이용해W , … ,W 를업데이트할수있다
W ← W − α =W − αδ z
δL
δℓ
δ1
= [diag(∇f (W z )) ⊙ ∇ L( )]L L (L−1) y y^
⋮
=W [diag(∇f (W z )) ⊙ δ ]ℓ+1
T
ℓ ℓ (ℓ−1) ℓ+1
⋮
=W [diag(∇f (W x)) ⊙ δ ]2
T
1 1 2
1 L
ℓ ℓ
∂Wℓ
∂L
ℓ ℓ (ℓ−1)
T