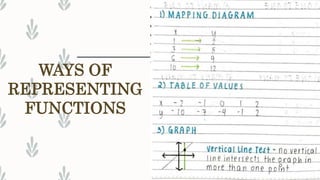
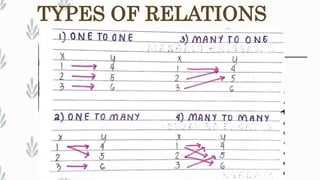
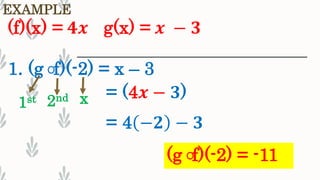1. The document discusses key concepts related to functions including relations, domains, ranges, and different ways of representing functions. 2. It provides examples and explanations of fundamental operations on functions including addition, subtraction, multiplication, division, and composition of functions. 3. The examples demonstrate how to perform each operation by substituting values, distributing terms, and combining like terms according to specific rules for exponents.

1. EVALUATING
FUNCTIONS

2. ALL FUNCTIONS ARE
RELATIONS BUT NOT ALL
RELATIONS ARE FUNCTIONS
“Lahat ng gumagana ay may
relasyon, pero hindi lahat ng
relasyon ay gumagana”

3. RELATION
a set of ordered pairs (x,y)
DOMAIN
first coordinate in a relation; (x);
input; independent.
RANGE
second coordinate in a relation; (y);
output; dependent.
FUNCTION
a relation in which each element in the domain
corresponds to exactly one of element of the range.

4. L
O
V
E
EXAMPLE
3
8
5
6
GERALD
Maja
Bea
Julia
Kim
Sarah
FUNCTION NOT
FUNCTION

5. WAYS OF
REPRESENTING
FUNCTIONS

6. TYPES OF RELATIONS

7. variable in the function
F (x) = 3x + 1
name of the function is f (g, h)

8. 1.) x = 2
EXAMPLE
f (x) = 7
f (2) = 3(2) + 1

9. 2.) x = 8
EXAMPLE
f (x) = 83
f (x) = 𝒙 𝟐
+𝟑𝒙 − 𝟓
= (𝟖) 𝟐
+𝟑(𝟖) − 𝟓
= 𝟔𝟒 + 𝟐𝟒 − 𝟓

10. 3.) x = 2 –x
EXAMPLE
f (x) = 𝒙 𝟐
−𝟒𝒙 + 𝟔
f (x) = 𝒙 𝟐
+𝟐
= (𝟐 − 𝒙) 𝟐+𝟐
= 𝟒 − 𝟐𝒙 − 𝟐𝒙 + 𝒙 𝟐
+𝟐

11. 4.) x = -5
EXAMPLE
f (x) = 𝟔𝟐
f (x) = 𝒙 𝟐
− 𝟖𝒙 − 𝟑
= 𝟐𝟓 + 𝟒𝟎 − 𝟑
= (−𝟓) 𝟐
−𝟖(−𝟓) − 𝟑

12. FUNDAMENTAL
OPERATIONS
OF
FUNCTIONS

13. ADDITION
 Substitute the value of 2
functions.
 Combine like terms.

14. 1.) f(x) = 𝟐𝒙 𝟑
−𝟓𝒙 + 𝟒
EXAMPLE
(f + g)(x) = 𝟐𝒙 𝟑
+ 𝟑𝒙 𝟐
− 𝟑𝒙 − 𝟔
(f + g)(x) = f(x) + g(x)
= ( 𝟐𝒙 𝟑
−𝟓𝒙 + 𝟒) + ( 𝟑𝒙 𝟐
+𝟐𝒙 − 𝟔)
g(x) = 𝟑𝒙 𝟐
+𝟐𝒙 − 𝟔

15. 2.) f(x) = 𝟐𝒙 − 𝟏
EXAMPLE
(f + g)(x) = 𝒙 𝟐
+𝟑𝒙 − 𝟑
(f + g)(x) = f(x) + g(x)
= ( 𝟐𝒙 − 𝟏) + ( 𝒙 𝟐
+ 𝒙 − 𝟐)
g(x) = 𝒙 𝟐
+ 𝒙 − 𝟐

16. 3.) f(x) = 𝟓 − 𝒙 𝟐
EXAMPLE
(f + g)(x) = 𝟒𝒙 − 𝟕
(f + g)(x) = f(x) + g(x)
= ( 𝟓 − 𝒙 𝟐
) + ( 𝒙 𝟐
+𝟒𝒙 − 𝟏𝟐)
g(x) = 𝒙 𝟐
+𝟒𝒙 − 𝟏𝟐

17. SUBTRACTION
 Substitute the value of 2
functions.
 Change the sign of the
subtrahend.
 Combine like terms.

18. 1.) f(x) = 𝟐𝒙 𝟑
−𝟓𝒙 + 𝟒EXAMPLE
(f – g)(x) = 𝟐𝒙 𝟑
− 𝟑𝒙 𝟐
− 𝟕𝒙 + 𝟏𝟎
= ( 𝟐𝒙 𝟑
−𝟓𝒙 + 𝟒) – ( 𝟑𝒙 𝟐
+𝟐𝒙 − 𝟔)
g(x) = 𝟑𝒙 𝟐
+𝟐𝒙 − 𝟔
(f – g)(x) = f(x) – g(x)
= ( 𝟐𝒙 𝟑
−𝟓𝒙 + 𝟒) + ( −𝟑𝒙 𝟐
−𝟐𝒙 + 𝟔)

19. 2.) f(x) = 𝟐𝒙 − 𝟏EXAMPLE
(f – g)(x) = −𝒙 𝟐
+ 𝒙 + 𝟏
= ( 𝟐𝒙 − 𝟏) + ( −𝒙 𝟐
− 𝒙 + 𝟐)
g(x) = 𝒙 𝟐
+ 𝒙 − 𝟐
(f – g)(x) = f(x) – g(x)
= ( 𝟐𝒙 − 𝟏) – ( 𝒙 𝟐
+ 𝒙 − 𝟐)

20. 3.) f(x) = 𝟓 − 𝒙 𝟐
EXAMPLE
(f – g)(x) = −𝟐𝒙 𝟐
− 𝟒𝒙 + 𝟏𝟕
(f – g)(x) = f(x) – g(x)
= (𝟓 − 𝒙 𝟐
) + ( −𝒙 𝟐
−𝟒𝒙 + 𝟏𝟐)
g(x) = 𝒙 𝟐
+𝟒𝒙 − 𝟏𝟐
= (𝟓 − 𝒙 𝟐
) – ( 𝒙 𝟐
+𝟒𝒙 − 𝟏𝟐)

21. QUIZ a. f(0)
b. f(-1)
c. f(2)
2.) f(x) = 2𝒙 − 𝟒 g(x) = 𝟑𝒙 − 𝟓
1.) f(x) = 𝒙 𝟐+𝟓𝒙 − 𝟑
ADDITION and SUBTRACTION

22. ASSIGNMENT To be submitted
tomorrow
WEDNESDAY
(SEPTEMBER 23, 2020)
UNTIL 5PM ONLY.

23. MULTIPLICATION
1.) Product Rule for
Exponent
Laws of Exponent
(𝒙 𝒎
) 𝒏
= 𝒙 𝒎𝒏2.) Power Rule for
Exponent
𝒙 𝒎
• 𝒙 𝒏
= 𝒙 𝒎+𝒏
3.) Power of a
Product Rule (𝒙𝒚) 𝒏
= 𝒙 𝒏
𝒚 𝒏

24. A. Multiplying a binomial to a
monomial
EXAMPLE
1.) f(x) = 𝟓𝒙 g(x) = 𝒙 + 𝟒
(f • g)(x) = f(x) • g(x)
= (𝟓𝒙) (𝒙 + 𝟒)
(f • g)(x) = 𝟓𝒙 𝟐 +𝟐𝟎𝒙

25. A. Multiplying a binomial to a
binomial (FOIL)
EXAMPLE
1.) f(x) = 𝒙 + 𝟑 g(x) = 𝒙 + 𝟓
(f • g)(x) = f(x) • g(x)
= 𝒙 𝟐+𝟓𝒙 + 𝟑𝒙 + 𝟏𝟓
(f • g)(x) = 𝒙 𝟐
+ 𝟖𝒙 + 𝟏𝟓
= (𝒙 + 𝟑) (𝒙 + 𝟓)

26. A. Multiplying a binomial to a
trinomial
EXAMPLE
1.) f(x) = 𝟗𝒙 + 𝟓 g(x) = 𝟔𝒙 𝟐
+ 𝒙 − 𝟓
(f • g)(x) = f(x) • g(x)
= 𝟓𝟒𝒙 𝟑
+𝟗𝒙 𝟐
− 𝟔𝟑𝒙 − 𝟑𝟎𝒙 𝟐
− 𝟓𝒙 + 𝟑𝟓
(f • g)(x) = 𝟓𝟒𝒙 𝟑
−𝟐𝟏 𝒙 𝟐
− 𝟔𝟖𝒙 + 𝟑𝟓
= (𝟗𝒙 + 𝟓) ( 𝟔𝒙 𝟐
+ 𝒙 − 𝟓)

27. DIVISION
1.)
𝒙 𝒎
𝒙 𝒏 = 𝒙 𝒎−𝒏
; 𝒘𝒉𝒆𝒏 𝒎 > 𝐧
Rules of Division of Exponent
2.)
𝒙 𝒎
𝒙 𝒏 =
𝟏
𝒙 𝒏−𝒎 ; 𝒘𝒉𝒆𝒏 𝒎 < 𝐧
3.)
𝒙 𝒎
𝒙 𝒏 = 𝒙 𝟎
= 𝟏; 𝒘𝒉𝒆𝒏 𝒎 = 𝟎

28. EXAMPLE
1.) f(x) = 𝟏𝟓𝒙 𝟏𝟓
g(x) = 𝟑𝒙 𝟗
𝒇
𝒈
𝒙 = 𝟓𝒙 𝟔
=
𝟏𝟓𝒙 𝟏𝟓
𝟑𝒙 𝟗𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)

29. EXAMPLE
2.) f(x) = −𝟒𝒙 𝟓
g(x) = 𝟐𝒙 𝟖
𝒇
𝒈
𝒙 =
−𝟐
𝒙 𝟑
=
−𝟒𝒙 𝟓
𝟐𝒙 𝟖
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)
= −𝟐(
𝟏
𝒙 𝟖−𝟓)
2.)
𝒙 𝒎
𝒙 𝒏 =
𝟏
𝒙 𝒏−𝒎 ; 𝒘𝒉𝒆𝒏 𝒎 < 𝐧

30. EXAMPLE
3.) f(x) = 𝟗𝒙 𝟔
g(x) = 𝟗𝒙 𝟔
𝒇
𝒈
𝒙 = 𝟏
=
𝟗𝒙
𝟔
𝟗𝒙 𝟔
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)
= 𝟏(𝒙 𝟎
) = 𝟏(𝟏)
3.)
𝒙 𝒎
𝒙 𝒏 = 𝒙 𝟎
= 𝟏; 𝒘𝒉𝒆𝒏 𝒎 = 𝟎

31. EXAMPLE
4.) f(x) =𝟐𝒙 − 𝟐
g(x) = 𝒙 𝟐
+𝟐𝒙 − 𝟑
𝒇
𝒈
𝒙 =
𝟐
𝒙 + 𝟑
=
𝟐𝒙 −𝟐
𝒙 𝟐+𝟐𝒙 −𝟑
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)
=
𝟐(𝒙 −𝟏)
(𝒙−𝟏)(𝒙 −𝟑)

32. EXAMPLE
5.) f(x) = 𝒙 − 𝟓 g(x)
= 𝟏𝟎𝒙 − 𝟓𝟎
𝒇
𝒈
𝒙 =
𝟏
𝟏𝟎
=
𝒙−𝟓
𝟏𝟎𝒙 −𝟓𝟎
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)
=
𝒙−𝟓
𝟏𝟎(𝒙 −𝟓)

33. COMPOSITION
 Write the given.
 Replace x by the 2nd function.
 Distribute
 Combine like/similar terms.
 Substitute the value of x.
 Solve and simplify.
(𝐟 °𝒈)(x)
1st 2nd
(𝐠 °𝒇)(x)
1st 2nd

34. EXAMPLE
(f )(x) = 𝟒𝒙 − 𝟓 g(x) = 𝒙 𝟐
+ 𝟒
1. (f g)(3) = 4x - 5
1st 2nd x
= 4(𝒙 𝟐
+ 𝟒) - 5
= 4𝒙 𝟐
+ 𝟏𝟔 − 𝟓
= 4𝒙 𝟐
+ 𝟏𝟏
= 4(𝟑) 𝟐
+𝟏𝟏
= 𝟑𝟔 + 𝟏𝟏 (f g)(3) = 47

35. EXAMPLE
(f)(x) = 𝟒𝒙 − 𝟓
g(x) = 𝒙 𝟐
+ 𝟒
2. (g f)(2) = 𝒙 𝟐
+ 𝟒
1st 2nd x
= (𝟒𝐱 − 𝟓 ) 𝟐
+ 𝟒
= 𝟏𝟔𝒙 𝟐 − 𝟐𝟎𝒙 − 𝟐𝟎𝒙 + 𝟐𝟓 + 𝟒
= 𝟏𝟔𝒙 𝟐
− 𝟒𝟎𝒙 + 𝟐𝟗
= 𝟔𝟒 − 𝟖𝟎 + 𝟐𝟗 (g f)(2) = 13
FOIL METHOD
= 𝟏𝟔(𝟐) 𝟐
−𝟒𝟎(𝟐) + 𝟐𝟗

36. EXAMPLE
(f)(x) = 𝟒𝒙 g(x) = 𝒙 − 𝟑
1. (f g)(-2) = 4x
1st 2nd x = 4(𝒙 − 𝟑)
= 4𝒙 − 𝟏𝟐
= 4 −𝟐 − 𝟏𝟐
(f g)(-2) = -20

37. EXAMPLE
(f)(x) = 𝟒𝒙 g(x) = 𝒙 − 𝟑
1. (g f)(-2) = x – 3
1st 2nd x = (4𝒙 − 𝟑)
= 4 −𝟐 − 𝟑
(g f)(-2) = -11

38. ASSIGNMENT!
IN YOUR BOOK ANSWER,
PAGE 3 # 1-3
PAGE 5-6 # 1-6

39. PROBLEM
SOLVING
INVOLVING
SETS
10/2/20

40. If 270 traveled to an event. There were 7
buses and 18 others in cars. Find the number
of people on each bus.
𝒙 = # 𝒐𝒇 𝒑𝒆𝒐𝒑𝒍𝒆 𝒐𝒏 𝒆𝒂𝒄𝒉 𝒃𝒖𝒔.
𝟕𝒙 + 𝟏𝟖 = 𝟐𝟕𝟎
𝟕𝒙 = 𝟐𝟕𝟎 − 𝟏𝟖
𝟕𝒙 = 𝟐𝟓𝟐
𝒙 = 𝟑𝟔
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝒕𝒉𝒆𝒓𝒆
𝒂𝒓𝒆 𝟑𝟔 𝒑𝒆𝒐𝒑𝒍𝒆
𝒐𝒏 𝒆𝒂𝒄𝒉 𝒃𝒖𝒔.

41. A plumber’s fees (F) are 50 for a house call
and 30 for each hour (H) worked.
𝟑𝟎𝒉 + 𝟓𝟎 = 𝒇
𝟑𝟎(𝟏) + 𝟓𝟎 = 𝒇
𝟖𝟎 = 𝒇
X Y
1
2
𝟑𝟎 + 𝟓𝟎 = 𝒇

42. The total cost (C) for pounds (p) of copper, if
each pound costs ₱5.67?
𝟓. 𝟔𝟕𝒑 = 𝑪
𝟓. 𝟔𝟕 𝟏 = 𝑪
𝟓. 𝟔𝟕 = 𝑪
X Y
1
2
3
4

43. ASSIGNMENT!
IN YOUR BOOK ANSWER,
PAGE 4: Letter B
# 1 & 2 ( A and B)