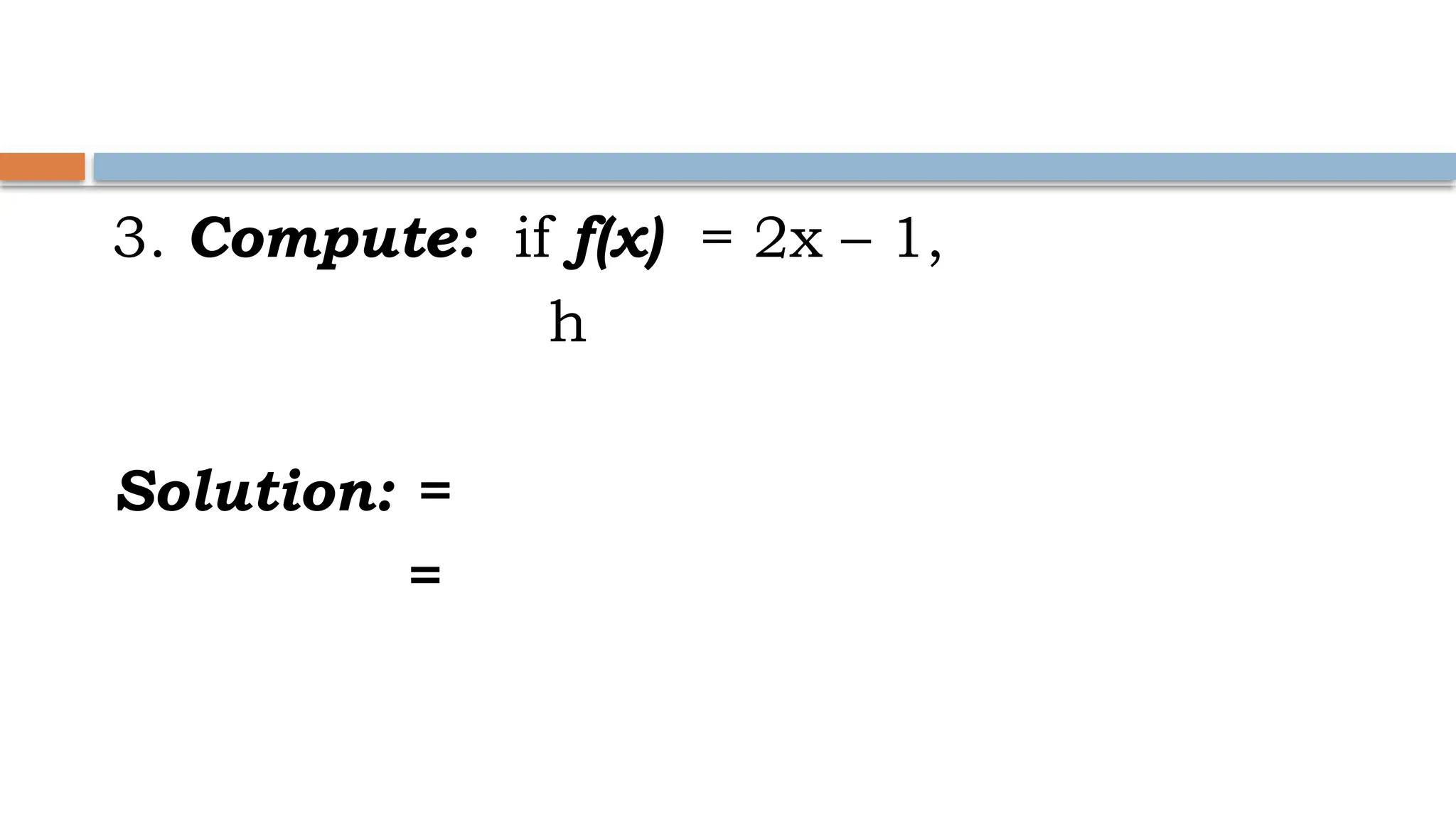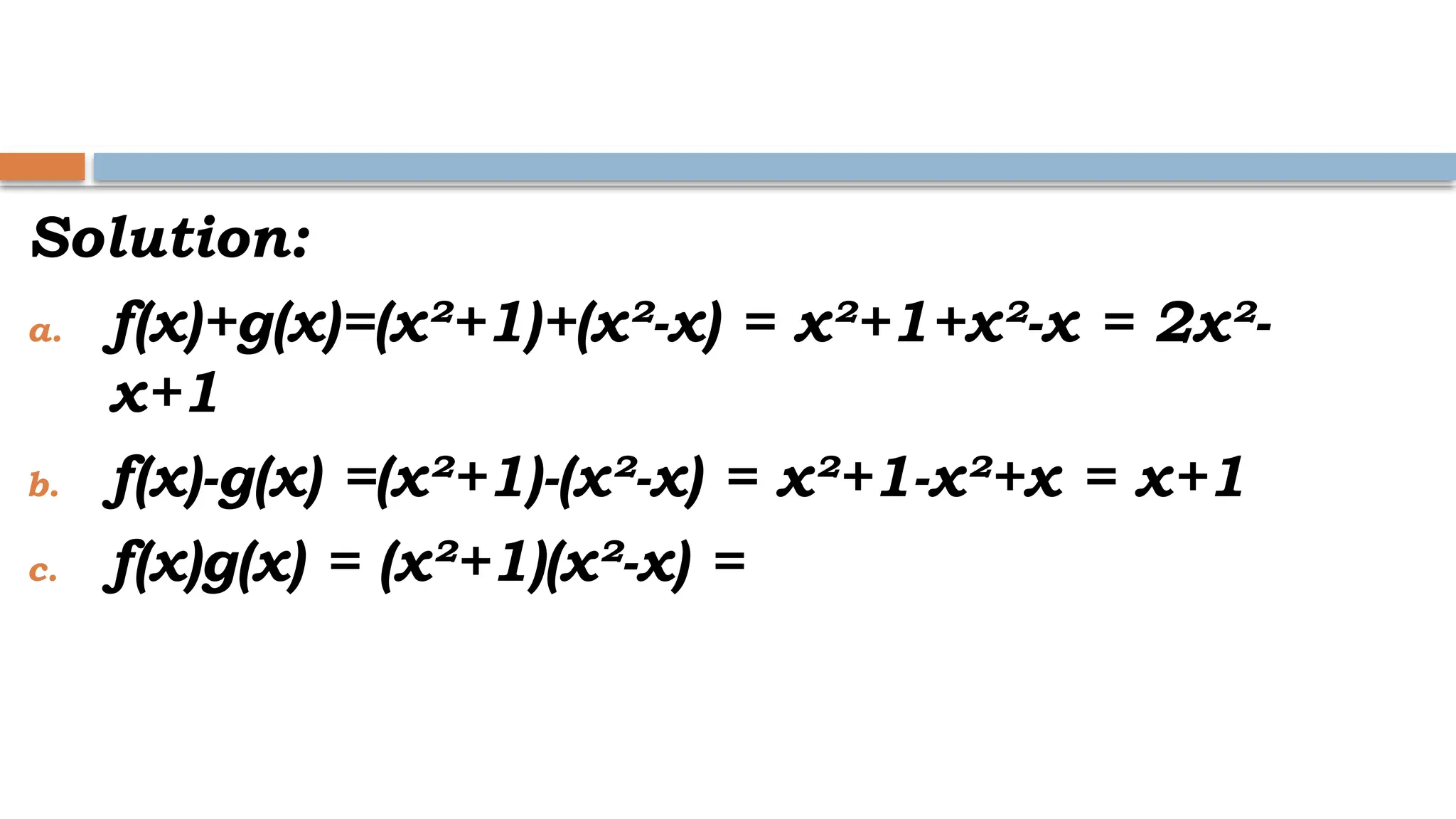The document explains binary operations on a set, describing how each pair of elements produces a unique response also within the set. It outlines operations such as addition, subtraction, multiplication, and division of functions, providing examples for each. Additionally, it includes specific calculations of function values and operations involving given functions.

1. BINARY OPERATION
JOHN CLIFFORD T. MORENO, LPT

2.  A binary operation *in a set S is a way of
assigning every ordered pair of elements,
a and b, from the set, a unique response
called c, where c is also from the set S.
a * b = c
First
element
from the set
operation Second
element from
the set
Unique
response
from the
set

3.  Binary operations include addition,
subtraction, multiplication and division.
 The value of f(x) is obtained upon
assigning a specific value for x. The
variable x represents the independent
variable and y represents the dependent
variable.

4.  Given y=f(x) and let a be in the domain
of f . Then f(a) represents the second
element in the pair of defining f, or the
value of the function at x = a. The value
of f(a) is obtained by replacing x by a in
f(x).

6. 1. Let f(x) = 2x³ - 3x² - 5x + 2.
Find: a. f(1)
b. (-1)
c. f(-3)

7. Solutions:
a. f(1) = 2(1)³-3(1)²-5(1)+2 = -4
b. f(-1) = 2(-1)³-3(-1)²-5(-1)+2 = 2
c. f(-3) = 2(-3)³-3(-3)²-5(-3) +2 = -64

8. 2. Let f(x) =
Find: a. f(2)
b. f
c. f(b)

9. Solution:
a. (2) =
b. f
c. f(b) =

10. 3. Compute: if f(x) = 2x – 1,
h
Solution: =
=

11. A binary operation on a set is a calculation involving two
elements of the set to produce another element of the set.
1. Given two functions : f(x) and g(x), then
2. Sum of two functions : f(x) + g(x)
3. Difference of two functions : f(x) – g(x)
4. Product of two functions : f(x)
5. Quotient of two functions : f(x)/g(x),
g(x)

12. Operations with Functions
We can add, subtract,
multiply and divide
functions!
The result is a new
function.

13. Example:
1. Given f(x) = x² + 1 and g(x) = x² - x
a. f(x) + g(x)
b. f(x) – g(x)
c. f(x) g(x)
d.

14. Solution:
a. f(x)+g(x)=(x²+1)+(x²-x) = x²+1+x²-x = 2x²-
x+1
b. f(x)-g(x) =(x²+1)-(x²-x) = x²+1-x²+x = x+1
c. f(x)g(x) = (x²+1)(x²-x) =

15. Addition of Function
 We can add two functions:
(f+g)(x) = f(x) + g(x)
Note:
we put the f+g inside () to show they
both work on x.

16. Example 1
Let f(x) = 2x+3 and g(x) = x2
Find (f+g)(x)
Solution:
(f+g)(x) = f(x) + g(x)
= (2x+3) + (x2)
= x2+2x+3

17. Example 2
Let v(x) = 5x+1 and w(x) = 3x-2
Find (v+w)(x)
Solution:
(v+w)(x) = v(x)+w(x)
=(5x+1) + (3x-2)
= 8x-1

18. Subtaction of Function
 We can subtract two functions:
(f-g)(x) = f(x) - g(x)
Note:
The difference f-g is a function whose domains are the set
of all real numbers common to the domain of f and g.

19. Example 3
let f(x) = x2
- 5 and g(x) = 5x -4
Find (f-g)(x)
Solution:
(f-g)(x) = f(x)-g(x)
=(x2
- 5) - (5x-4)
=x2
- 5 - 5x +4
=x2
- 5x - 1

20. Multiplication of Function
We can multiply two functions:
(f•g)(x) = f(x) • g(x)
Note:
The product f•g is a function whose domains
are the set of all real numbers common to the
domain of f and g.

21. Example 4
Let f(x) = 3x - 2 and g(x) = x2
- 2x - 3
Find (f•g)(x)
Solution:
(f•g)(x) = f(x)•g(x)
=(3x - 2) (x2
- 2x - 3)
=3x(x2
- 2x - 3) - 2(x2
- 2x - 3)
=3x3
- 6x2
- 9x - 2x2
+4x + 6
=3x3
-8x2
-5x +6

22. Division of Function
We can divide two functions:
(f/g)(x) = f(x) / g(x)
Note:
The quotient f/g is a function whose
domains are the set of all real numbers
common to the domain of f and g. Where
g(x) or denomenator ≠ 0.

23. Example 5
Let f(x) = x + 3 and g(x) = x2
+ x - 9
Find (f/g)(x)
Solution:

24. ACTIVITY 3!
Q: Sir kanus-a ipass?
A: I-pass ni siya dungan sa
midterm napod nga activities

25. Directions: Perform the given operation.
1. f(x) =2x – 5, g(x) = 3x – 4
a. f(x) + g(x)
b. f(x) – g(x)
c. f(x) g(x)
d. f(x)/g(x)
2. f(x)=x²-4, g(x) =x+2
a. f(x) + g(x)
b. f(x) – g(x)
c. f(x) g(x)
d. f(x)/g(x)