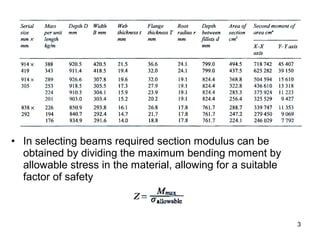
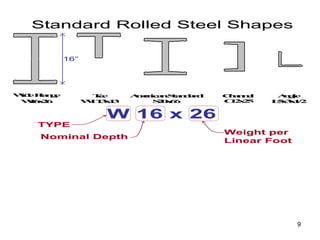
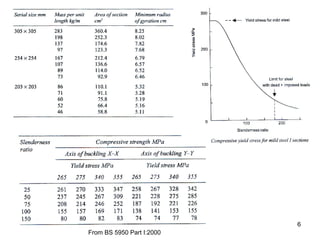
This document discusses the selection and design of standard steel beams and columns. It provides information on: 1) How to select standard steel sections from reference tables that list section properties like elastic section modulus. 2) How to calculate required section modulus based on maximum bending moment and allowable stress. 3) Guidelines for selecting sections, including choosing sections that minimize weight for beams and have slenderness ratios below 180 for columns. 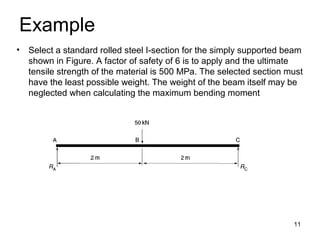4) An example of designing a simply supported beam by calculating bending moment, allowable stress, and required section modulus.

1. Chapter 1- Static engineering systems
1.2 Beams and columns
1.2.1 elastic section modulus for beams
1.2.2 standard section tables for rolled steel
beams
1.2.3 selection of standard sections (eg
slenderness ratio for compression
members, standard section and allowable
stress tables for rolled steel columns,
selection of standard sections)
1

2. Standard sections
• Standard section handbooks give values of section
modulus for different section beams
• Such data and guidance on the design of structures are
given in British Standards and relevant ones for design
using beams are BS 4 Part I:2005 (structural steel
sections) and BS 5950 Part I:2000 (structural use of
steelwork in building, code of practice for design, rolled
and welded sections)
• Example type of data sheet is illustrated on the next slide
2

3. • In selecting beams required section modulus can be
obtained by dividing the maximum bending moment by
allowable stress in the material, allowing for a suitable
factor of safety
3

4. • If the allowable stresses are the same for both tension and
compression, then a cross-sectional shape which has its neutral axis
at the mid height of the beam selected
• To minimize the weight of a beam, abeam can be selected that has
not only has the required sectional modulus but also the smallest
cross-sectional area and the smallest mass per unit length
• The critical buckling stress depends on the material concerned and
how a slender a column is. The measure of slenderness used in the
slenderness ratio.
where the effective length is essentially the length between points at
which the member bows about. (eg: both ends fixed effective length is
0.70L, One end fixed and other end pinned 0.85L, vertical cantilever
2L)
4

5. Radius of gyration
5

6. 6
From BS 5950 Part I:2000

7. • The maximum slenderness ratio for steel columns carrying dead and
imposed loads is limited to 180; as table and graph indicates, when the
slenderness ratio approaches this value the compressive strength drops to
a quite a low value.
• If in the design of structure, a larger slenderness ratio is indicated and it
indicates the need to use a larger section size in order to decrease the
slenderness ratio
• The general procedure for designing axially loaded column is
– Determine the effective length of the required column
– Select a trial section
– Using the radius of gyration value for the trial section, calculate the slenderness
ratio
– If the slenderness ratio is greater than 180, try a large cross section trial section
– Using the slenderness ratio, obtain the compression strength from the tables
– Compare the compression strength with that which is likely to be required in
practice. If the compression strength is adequate then the trial section is suitable.
If the compression strength is much greater than is required then it would be
more economical to choose a section with a smaller radius of gyration.
7

8. 8

9. Standard Rolled Steel Shapes
16”
W eF n e
id l g
a Te
e A e i a Sa d r
m c n t n ad
r Ca nl
hn e Age
nl
W x6
1 2
6 W 1 x3
T 31 S0 6
2x6 C2 2
1x5 Lx x /
5 3 12
W 16 x 26
TYPE
Weight per
Nominal Depth
Linear Foot
9

10. Steps to design beams for bending
1. For a given loading determine draw the Bending Moment Diagram (BMD) and
determine Mmax.
2. Specify the type of material to be used and determine the allowable bending
stress σall based on the ultimate stress σ ult and a selected factor of safety FS
(e.g.: σ all = σ ult/ FS).
3. Determine the required cross section modulus S using equation (1) that will
ensure that σ max is NOT more than σ all.
S = Mmax / σ all … (1)
4. For standard cross section (including I-shaped, S-cross sections, Wide-flange
cross sections), some design tables often tabulate the values of section
modulus for each shape. The design will then only requires selecting a suitable
economical shape (e.g.: WF-shape or I-shape) such that the selected cross
section will ensure that
Sprovided ≥ Srequired … (2)
4. Then if inequality (2) above is satisfied, the beam stresses will also satisfy the
following design requirements
σ max ≤ σ all … (3)
As the design process is often iterative (repetitive), the above steps might
have to be repeated till the requirements of inequalities 2 and 3 above are
satisfied and the cross section is economical to construct with minimum cost
10
(very often it is the cross section with minimum weight).

11. Example
• Select a standard rolled steel I-section for the simply supported beam
shown in Figure. A factor of safety of 6 is to apply and the ultimate
tensile strength of the material is 500 MPa. The selected section must
have the least possible weight. The weight of the beam itself may be
neglected when calculating the maximum bending moment
11

12. • Finding support reactions:
The beam is symmetrically loaded and so the support reactions R A and
RC will be equal. That is,
RA = RC = 50/2
RA=RC=25 kN
• Finding maximum bending moment, M which will be at the centre of the
beam:
M = RA X 2 = 25 X 103 X 2
M =50X 103Nm
• Finding maximum allowable stress, σ:
• Finding elastic section modulus, s:
s
s 12

13. • Multiply by 106 to convert section modulus to cm 3:
s
s
• Finding section with next higher value and least mass per
meter from standard section table:
s
13