Downloaded 684 times
Uploaded byS M Rahat Rahman
T BEAM (ULTIMATE STRENGTH DESIGN)
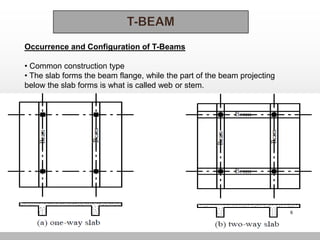
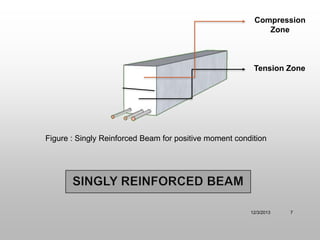
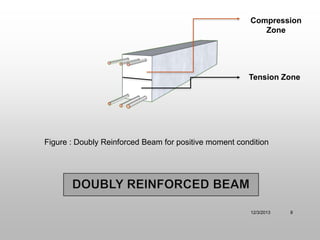
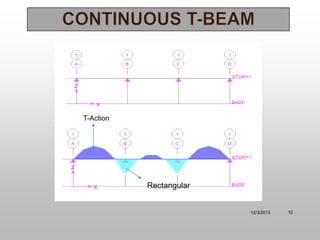
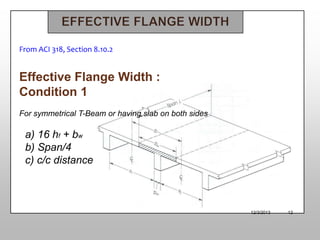
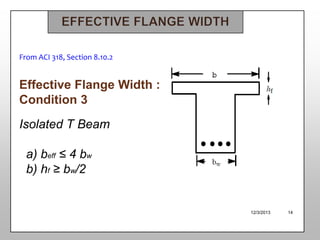
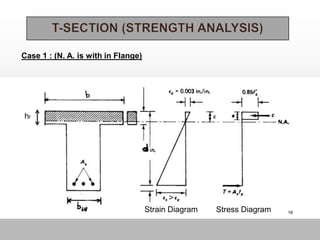
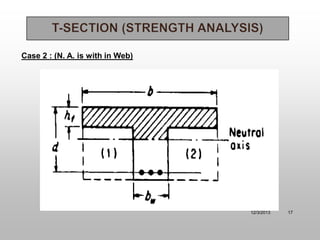
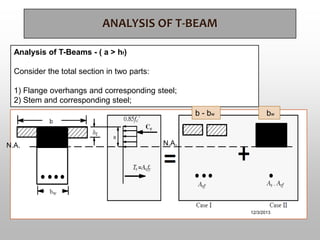
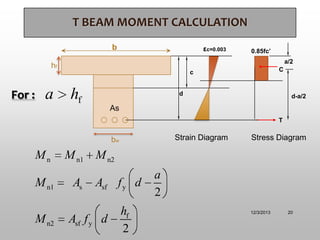
The document discusses T-beam design in the context of civil engineering, focusing on singly and doubly reinforced beams. It outlines the importance of concrete beams being cast integrally with slabs, how they function under different bending moments, and the ACI code guidelines for determining effective flange width. Additionally, it includes analysis methods for T-beams and moment calculation techniques.
More Related Content
Similar to T BEAM (ULTIMATE STRENGTH DESIGN)
T BEAM (ULTIMATE STRENGTH DESIGN)
- 1. AHSANULLAH UNIVERSITY OF SCIENCE& TECHNOLOGY DEPARTMENT OF CIVIL ENGINEERING CE-416 PRE-STRESSED CONCRETE LAB SESSIONAL PRESENTED BY: S. M. RAHAT RAHMAN ID NO:10.01.03.044 COURSE TEACHERS: MUNSHI GALIB MUKTADIR SABREENA NASRIN 12/3/2013 1
- 2. T BEAM DESIGN: SINGLY & DOUBLY : USD 12/3/2013 2
- 3.
- 4. Assuming tensilefailure condition Additional strength of steel after yielding ACI code emphasizes this method. 12/3/2013 4
- 5. Concrete beamsare often casted integrally with the slab and formed a “T” – shaped beam. These beams are very efficient . Here slab portion carries the compressive load and web portion carries the tension . 12/3/2013 5
- 6. Occurrence and Configurationof T-Beams • Common construction type • The slab forms the beam flange, while the part of the beam projecting below the slab forms is what is called web or stem. 12/3/2013 6
- 7. Compression Zone Tension Zone Figure :Singly Reinforced Beam for positive moment condition 12/3/2013 7
- 8. Compression Zone Tension Zone Figure :Doubly Reinforced Beam for positive moment condition 12/3/2013 8
- 9.
- 10.
- 11. T Versus RectangularSections When T-shaped sections are subjected to negative bending moments, the flange is located in the tension zone. On the other hand, when sections are subjected to positive bending moments, the flange is located in the compression zone and the section is treated as a Tsection. 12/3/2013 11
- 12. From ACI 318,Section 8.10.2 Effective Flange Width : Condition 1 For symmetrical T-Beam or having slab on both sides a) 16 hf + bw b) Span/4 c) c/c distance 12/3/2013 12
- 13. From ACI 318,Section 8.10.2 Effective Flange Width : Condition 2 Beams having slabs on one side only a) bw + span/12 b) bw + 6hf c) bw + 1/2 * beam clear distance 12/3/2013 13
- 14. From ACI 318,Section 8.10.2 Effective Flange Width : Condition 3 Isolated T Beam a) beff ≤ 4 bw b) hf ≥ bw/2 12/3/2013 14
- 15.
- 16. Case 1 :(N. A. is with in Flange) hf Strain Diagram Stress Diagram 12/3/2013 16
- 17. Case 2 :(N. A. is with in Web) 12/3/2013 17
- 18. ANALYSIS OF T-BEAM Analysisof T-Beams - ( a > hf) Consider the total section in two parts: 1) Flange overhangs and corresponding steel; 2) Stem and corresponding steel; b - bw N.A. bw N.A. 12/3/2013
- 19. ANALYSIS OF TBEAM Case-1 0.85 fc’ (b-bw) hf = As2 fy Where, As1 = As – Asf As2 = Asf Case-2 0.85 fc’ bw a = As1 fy 0.85 fc’ bw a + 0.85 fc’ (b-bw) hf = As fy 12/3/2013 19
- 20. T BEAM MOMENTCALCULATION b εc=0.003 0.85fc’ a/2 hf C c For : a hf d d-a/2 As T Strain Diagram bw Mn M n1 M n2 Stress Diagram M n1 M n2 As Asf f y d Asf f y d hf 2 a 2 12/3/2013 20
- 21.
- 22.
Editor's Notes
- #5 Based on the ultimate strength of the structure member assuming a failure condition , due to concrete crushing or yielding of steel. Although there is additional strength of steel after yielding (strain hardening zone) which will not be considered in the design.Actual loads are multiplied by load factor to obtain the ultimate design loads. ACI code emphasizes this method.
- #6 DefinitionFor monolithically casted slabs, a part of a slab act as a part of beam to resist longitudinal compressive force in the moment zone and form a T-Section. This section form the shape of a "T“ Concrete beams are often poured integrally with the slab, forming a much stronger “T” – shaped beam. These beams are very efficient because the slab portion carries the compressive loads and the reinforcing bars placed at the bottom of the stem carry the tension. A T-beam typically has a narrower stem than an ordinary rectangular beam. These stems are typically spaced from 4’-0” apart to more than 12’-0”. The slab portion above the stem is designed as a one-way slab spanning between stems.
- #7 Occurrence and Configuration of T-Beams• Common construction type.- used in conjunction with either on-way or two-way slabs.• Sections consists of the flange and web or stem; the slab forms the beam flange, whilethe part of the beam projecting below the slab forms is what is called web or stem.
- #8 A singly reinforced beam is one in which the concrete element is only reinforced near the tensile face and the reinforcement, called tension steel, is designed to resist the tension.
- #9 A doubly reinforced beam is one in which besides the tensile reinforcement the concrete element is also reinforced near the compressive face to help the concrete resist compression. The latter reinforcement is called compression steel. When the compression zone of a concrete is inadequate to resist the compressive moment (positive moment), extra reinforcement has to be provided if the architect limits the dimensions of the section.
- #10 T Beam acts as a singly reinforced beam . Because here exits slab and beam portion , which can easily resist the upcoming compressive load. So that extra reinforcement is not required in the compression zone . That’s why , T beam also serves the economic purpose .
- #12 T- versus Rectangular SectionsWhen T-shaped sections are subjected to negative bending moments, the flange is located in the tension zone. Since concrete strength in tension is usually neglected in strength design, the sections are treated as rectangular sections.On the other hand, when sections are subjected to positive bending moments, the flange is located in the compression zone and the section is treated as a T-section.
- #13 For symmetrical T-Beam or having slab on both sides a) 16 hf + bw b) Span/4 c) c/c distance (smallest value should be taken)
- #14 Beams having slabs on one side only a) bw + span/12 b) bw+ 6hf c) bw+ 1/2 * beam clear distance (smallest value should be taken)
- #15 Isolated T Beam a) beff ≤ 4 bw b) hf ≥ bw/2 (smallest value should be taken)
- #16 Analyse as a rectangular beam of width𝑏=𝑏𝑒𝑓𝑓𝑀𝑛= 𝐴𝑠 𝑓𝑦 (𝑑− 𝑎2)Analyse as a rectangular beam of width 𝑏=𝑏𝑒𝑓𝑀𝑛= 𝐴𝑠 𝑓𝑦 (𝑑− 𝑎/2)
- #17 T beam may be treated as a rectangular if stress block depth a ≤ hfand as a T beam If a >hf .Nominal moment , Mn = 〖 𝐴〗_𝑠 𝑓_(𝑦 )(𝑑 − 𝑎/2)
- #18 T beam may be treated as a rectangular if stress block depth a ≤ hfand as a T beam If a >hf .T beam may be treated as a rectangular if stress block depth a ≤ hfand as a T beam If a >hf .Nominal moment , Mn = 〖 𝐴〗_𝑠 𝑓_(𝑦 )(𝑑 − 𝑎/2)