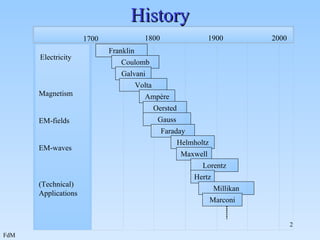
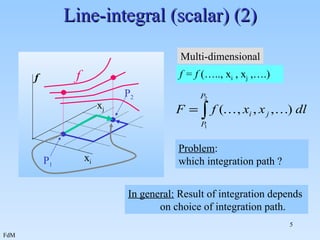
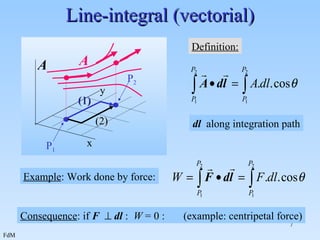
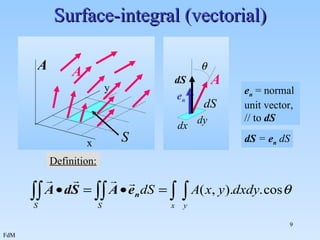
1. The document introduces various types of integrals used in electromagnetism, including line integrals, surface integrals, and volume integrals. 2. Examples are provided for calculating line integrals of scalar and vector fields, surface integrals of scalar and vector fields, and volume integrals of scalar fields. 3. The examples demonstrate calculating the integrals for different paths and surfaces in order to determine values like average temperature, work done by a force, and total charge in a region.

1. Electromagnetism First-year course on Integral types © Frits F.M. de Mul

2. History Electricity Magnetism EM-fields EM-waves (Technical) Applications Franklin Coulomb Galvani Volta Ampère Oersted Gauss Faraday Helmholtz Maxwell Lorentz Hertz Millikan Marconi 1700 1800 1900 2000

3. Multidimensional integrations Integration of charges and currents over lines, planes and volumes Line integrals (scalar, vectorial) +example Surface-integrals (scalar, vectorial) + 2 examples Volume-integrals (scalar only) + example

4. Line-integral (scalar) (1) Example: Calculate average temperature T (x) between x 1 and x 2 Meaning of F: y x x 1 x 2 f (x) One-dimensional: F F = area under curve

5. Line-integral (scalar) (2) Problem : which integration path ? In general: Result of integration depends on choice of integration path. f x i x j P 1 P 2 f f = f (….., x i , x j ,….) Multi-dimensional

6. Line-integral (scalar) (3) Special case: Conservative field: result in dependent of path T x y P 1 P 2 T T (x,y) = c (2x+y) P 1 (1,1) P 2 (2,3) Example (1) (2) (1) (2) Different paths : different results; Calculate line-integrals first and check below:

7. Line-integral (vectorial) dl along integration path Consequence : if F  dl : W = 0 : (example: centripetal force) A x y P 1 P 2 A (1) (2) Example : Work done by force: Definition:

8. Surface-integral (scalar) T x y P 1 P 2 T Temperature field: T = f (x,y) = c(2x+y) Problem: determine < T > over S; Find formula and calculate: S

9. Surface-integral (vectorial) Definition: A e n  dx dy dS e n = normal unit vector, // to dS dS = e n dS dS A x y A S

10. Surface Integral (vectorial): Example 1 Contribution from  -component ( // e z ) only ! Calculate surface integral over x = 1..2 and y = 1..3 A x y A S A e n  dx dy dS e n = normal unit vector, // to dS dS = e n dS dS Suppose: Area S in z= 0 plane ; there A (x,y,0) = x e x + 2y e y + 3 e z

11. Surface Integral (vectorial): Example 2 dA = u.v = (R.sin  .d  ).(Rd  ) B Suppose : B = r. sin  e r + cos  e  + tan  e  Normal vector e n = e r everywhere ! R  d   d  R.sin  u v Spherical surface element Calculate surface integral of B over A at radius r over octant (  = 0 .. ½  ;  = 0.. ½  )

12. Volume-integral (scalar only) Example: Charge density:  = c(3x-2y+5z) [C/m 3 ] Problem : determine total charge Q in V x y z V Block V : limited by points (1,1,1) and (2,4,5) dV=dxdydz Define charge element dQ in volume element dV : dQ =  .dV

13. Volume integral: Example Suppose: charge density  =3ar. sin  .cos  [C/m 3 ] Calculate charge Q in region: ( 2<r<3 ; 0<  < ½  ; - ½  <  < ½  ) the end r  d   d  r.sin  u v Spherical volume element w R dV = u.v.w = ( r .sin  . d  ).( rd  ). dr 0<  < 2  ; 0<  <  ; 0 < r < R