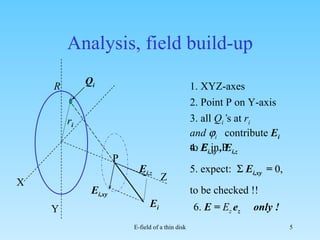
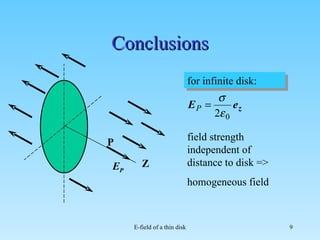
1. The document calculates the electric field (E-field) of a thin circular disk with a uniform charge density. 2. It sets up cylindrical coordinates and notes that due to the disk's symmetry, the only non-zero component of the E-field is Ez, along the z-axis perpendicular to the disk. 3. It describes calculating the E-field by integrating the contribution of elemental charge rings on the disk, showing that the E-field strength is independent of distance from the disk.

1. Electrical Field of a thin Disk © Frits F.M. de Mul

2. E -field of a thin disk Question : Calculate E -field in arbitrary points a both sides of the disk Available : A thin circular disk with radius R and charge density  [C/m 2 ]

3. E -field of a thin disk Analysis and symmetry Approach to solution Calculations Conclusions Appendix: angular integration

4. Analysis and Symmetry 1. Charge distribution:   C/m 2 ] 3. Symmetry: cylinder 4. Cylinder coordinates: r, z  2. Coordinate axes: Z-axis = symm. axis, perpend. to disk Z X Y e r r e z z e  

5. Analysis, field build-up 5. expect:  E i,xy = 0, to be checked !! 6. E = E z e z only ! R 1. XYZ-axes Z Y X 2. Point P on Y-axis P E i Q i r i 3. all Q i ’ s at r i and  i  contribute E i to E in P 4. E i,xy , E i,z E i,z E i,xy

6. Approach to solution R Z 2. Distributed charges dQ 3. dE e r r P 1. Rings and segments 4. dQ =  dA=  da.)(a d  a d   da 5. z - component only ! dE xy dE z 6.

7. Calculations (1) 2. dQ =  dA=  da.)(a d  R Z dQ dE e r r P a d   da dE z  z P 1. 3. 4.

8. Calculations (2) 6. If R  infinity : R Z dQ dE e r r P a d   da dE z  z P 4.

9. Conclusions field strength independent of distance to disk => homogeneous field Z P E P for infinite disk:

10. Appendix: angular integration (1) 2. dQ =  dA=  da.)(a d  R Z dQ dE e r r P a d   da dE z  z P 1. 

11. Appendix: angular integration (2) the end R Z dQ dE e r r P a d   da dE z  z P 