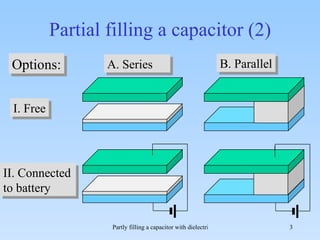
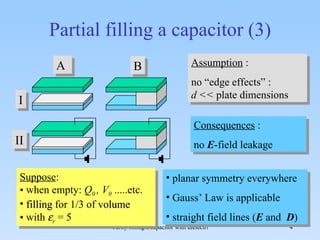
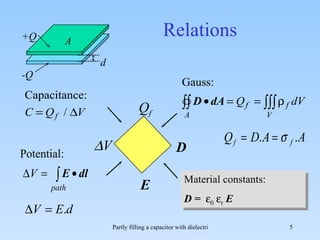
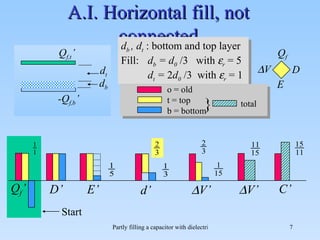
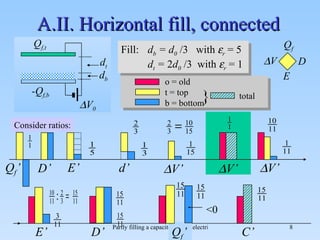
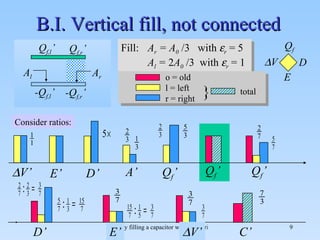
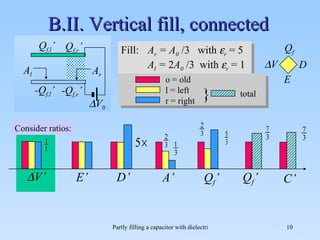
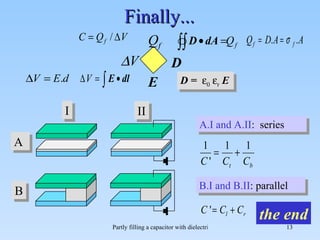
The document discusses the effects of partial filling a capacitor with dielectric material on various electrical parameters such as charge, potential difference, and capacitance. It presents different filling configurations (horizontal and vertical) and their implications on charge and potential when connected and disconnected from a battery. Key relationships and equations are provided for both series and parallel arrangements of capacitors during partial filling.

1. Filling a capacitor with a dielectric II: Partial filling © Frits F.M. de Mul

2. Partial filling a capacitor (1) Available: Flat capacitor : = surface area A , = distance of plates d , = no fill (  r  . Question: What will happen with Q ,  E, D,  V and C upon PARTIAL filling the capacitor with dielectric material (with  r  A d Assume: initially, plates are charged with +Q , -Q. +Q -Q

3. Partial filling a capacitor (2) A. Series B. Parallel I. Free II. Connected to battery Options:

4. Partial filling a capacitor (3) Suppose : when empty: Q 0 , V 0 .....etc. filling for 1/3 of volume with  r = 5 Assumption : no “edge effects” : d << plate dimensions Consequences : no E -field leakage planar symmetry everywhere Gauss’ Law is applicable straight field lines ( E and D ) A B I II

5. Relations Q f A d +Q -Q D E Material constants: D =    r  E  V

6. Options: main features A.I and B.I : total charge unchanged A.II and B.II : total potential unchanged A.I and A.II : potentials in series B.I and B.II : potentials parallel Suppose : when empty: Q 0 , V 0 ...... when filled: Q’, V’ , ...... filling for 1/3 of volume (depth or surface area) with  r = 5 A B I II

7. A.I. Horizontal fill, not connected d b , d t : bottom and top layer Fill: d b = d 0 /3 with  r = 5 d t = 2 d 0 /3 with  r = 1 Q f ’ D’ E’ d’  V’  V’ C’ Start Q f D E  V d b d t Q f,t ’ -Q f,b ’ o = old t = top b = bottom } total

8. A.II. Horizontal fill, connected Fill: d b = d 0 /3 with  r = 5 d t = 2 d 0 /3 with  r = 1 Q f ’ D’ E’ d’  V’  V’ C’  V’ E’ D’ Q f ’ Consider ratios: Q f D E  V d b d t Q f,t -Q f,b  V 0 o = old t = top b = bottom } total <0

9. B.I. Vertical fill, not connected Fill: A r = A 0 /3 with  r = 5 A l = 2 A 0 /3 with  r = 1 Q f ’ D’ E’ Consider ratios:  V’ A’ Q f D E  V E’ C’ o = old l = left r = right } total Q f,l ’ -Q f,r ’ Q f,r ’ -Q f,l ’ A l A r Q f ’ Q f ’ D’  V’

10. B.II. Vertical fill, connected Fill: A r = A 0 /3 with  r = 5 A l = 2 A 0 /3 with  r = 1 Q f ’ D’ E’ C’ Consider ratios:  V’ A’ Q f ’ Q f D E  V o = old l = left r = right } total Q f,l ’ -Q f,r ’ Q f,r ’ -Q f,l ’ A l A r  V 0

11. Options: overview C : 15/11 x Q f : unchanged  V : 11/15 x  V : unchanged Q f : 15/11 x C : 7/3 x Q f : unchanged  V : 3/7 x  V : unchanged Q f : 7/3 x B B.I and B.II : potentials parallel A A.I and A.II : potentials in series I II

12. With combination rules Filling with  r =5 in 1/3 of volume B B.I and B.II : parallel A A.I and A.II : series I II

13. Finally... the end D =    r  E B B.I and B.II : parallel A A.I and A.II : series I II Q f D E  V