Basics of Electronics measurements and instrumentation

1. EC410501
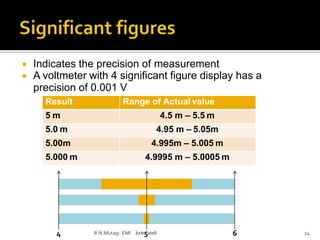
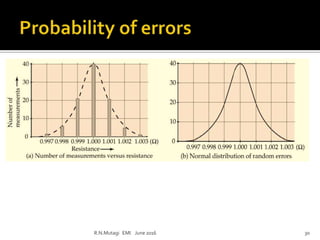
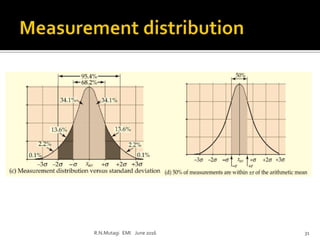
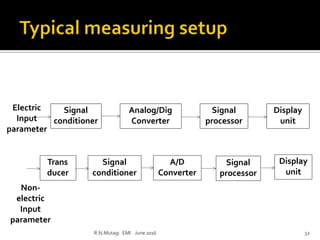
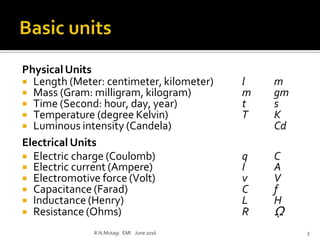
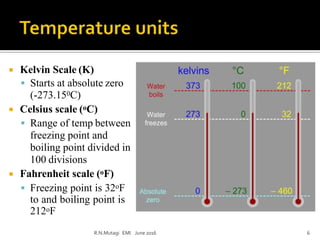
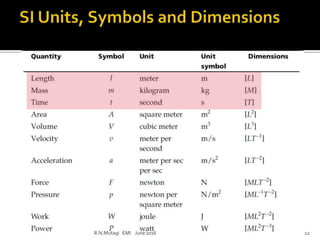
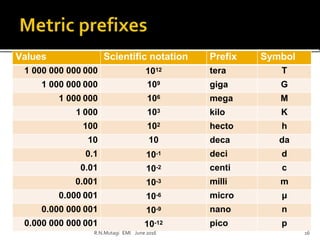
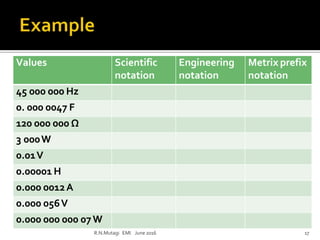
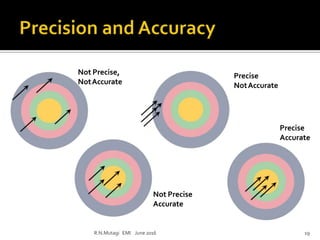
Electronic Measurements and Instruments
Department of Electronics and Communication Engineering
Indus Institute ofTechnology andEngineering
Indus University

2.  Units
 Standards
 Accuracy, precision, resolution
 Notations
 Electronic measurements
R.N.Mutagi EMI June 2016 2

3. PhysicalUnits
 Length (Meter: centimeter, kilometer) l m
 Mass (Gram: milligram, kilogram) m gm
 Time (Second: hour, day, year) t s
 Temperature (degree Kelvin) T K
 Luminous intensity (Candela) Cd
Electrical Units
 Electric charge (Coulomb) q C
 Electric current (Ampere) I A
 Electromotive force (Volt) v V
 Capacitance (Farad) C f
 Inductance (Henry) L H
 Resistance (Ohms) R ῼ
R.N.Mutagi EMI June 2016 3

4.  Meter (m): Length = 1650 763 times the λ of radiation
corresponding to transition between 2p10 and 5 d5 of
krypton-86 atom
 Kilogram (kg): Mass = the mass of international
prototype of mass of 1 kg
 Second (s): Duration of 9,192,631770 times
corresponding to the transition between two hyperfine
states of the ground level of Cesium -133 atom.
 Ampere ( A): Constant current maintained in 2 straight
parallel conductors of infinite length and negligible
circular cross section and placed 1 m apart in vacuum,
would produce between them a force of 2x 10-7
Newtons/meter length
R.N.Mutagi EMI June 2016 4

5.  Kelvin (K): Unit of thermodynamic temperature is the
fraction 1/273.16 of thermodynamic temperature of the
triple point of water.
 Candela (cd): Unit of intensity. One cd is the luminous
intensity, in the perpendicular direction, of a surface at
1/600000 m2 of a blackbody at the temperature of
freezing platinum under a pressure of 101,325
newtons/m2
R.N.Mutagi EMI June 2016 5

6.  Kelvin Scale (K)
 Starts at absolute zero
(-273.150C)
 Celsius scale (oC)
 Range of temp between
freezing point and
boiling point divided in
100 divisions
 Fahrenheit scale (oF)
 Freezing point is 32oF
to and boiling point is
212oF
R.N.Mutagi EMI June 2016 6

7.  Newton (N): Unit ofForce
 1 N is a force that gives a mass of 1 kg an acceleration of1
meter per sec persec
 Force = mass x acceleration, F =ma
 Joule (J): Unit ofWork
 1 joule is the amount of work done when a force of 1 Nacts
through a distance of 1 m
 Work = Force x distance, W =F.d
 Watts (W): Unit ofPower
 1W is the power developed when 1 joule of work is donein
1 second
 Power = work/ time, P =W /t
R.N.Mutagi EMI June 2016 7

8.  Ampere (A): Unit of electric current
 It is the constant current which
when flowing in each of two
infinitely long parallel conductors 1
meter apart, exerts a force of 2 x
10-7 Newtons per meter of lengthof
each conductor
 Coulomb (C): Unit of electric charge
 When a current of 1 A flows 1
coulomb of charge passes a given
point in a conductor
 Ampere = coulomb / second
R.N.Mutagi EMI June 2016 8

9.  Volt (V): Unit of emf and potential difference
 It is the potential difference between two points on a
conductor carrying a constant current of 1 Awhen power
dissipated between these points is 1Watt
 Ohm (Ω): Unit of resistance
 It is the resistance that permits the flow of 1 A current
through it when a potential difference of 1 V isapplied
across it
 Siemens (G): Unit of conductance
 It is the reciprocal of resistance
R.N.Mutagi EMI June 2016 9

10.  Henry (H): Unit of Inductance
 It is the inductance in which 1Volt emf is induced by a
current changing at 1A/s
 Farad (F): Unit of Capacitance
 It is the capacitance that contains a charge of 1 coulomb
when the potential difference across it is 1 V
 Weber (Wb): Unit of Magnetic Flux
 It is the magnetic flux, which linking a single-turn coil,
produces 1 V emf when flux is reduced to 0 at a constant
rate in 1 s.
 Tesla (T): Unit of Magnetic Flux Density
 It is the flux density of 1 Wb/m2
R.N.Mutagi EMI June 2016 10

11. Standard of measurement is a physical representation of a unit of
measurement
 International standards
 Defined by international agreement, maintained by
International Bureau of weight and measures in Paris
 Primary standards
 Maintained at National Bureau of Standards. Used for calibration
and verification of secondary standards
 Secondary standards
 Used by measurement and calibration laboratories in industry
 Working standards
 Principle tools in measurements laboratories
R.N.Mutagi EMI June 2016 11

12. R.N.Mutagi EMI June 2016 12

13. R.N.Mutagi EMI June 2016 13

14.  Logarithmic notation often used in expressing measured
results
 Ex. Gain = output power / input power
Gain-dB = 10 log (output power / input power)
 dB is dimensionless
 Then what are dBm, dBW, dBHz, dBi ?
 Remember
 log(1/x) = - log(x)
 log(xy) = y.log(x)
 log(x.y) = log(x) + log(y)
R.N.Mutagi EMI June 2016 14

15.  Scientific notation
 Very small and large numbers are expressed as a
number multiplied by 10 raised to a power
 Ex. 1400 = 1.4 x 103, 0.0047 = 4.7 x 10-3
 Engineering notation
 The power of 10 is a multiple of 3
 Ex. 140000 = 140 x 103, 14x108 = 1.4x109
0.00047 = 47x 10-6
 Metric prefix notation
 Symbols of metric prefix are employed
 Ex.140 kΩ, 4.2 GHz, 0.47µF, 2.7 nH
R.N.Mutagi EMI June 2016 15

16. Values Scientific notation Prefix Symbol
1 000 000 000 000 1012 tera T
1 000 000 000 109 giga G
1 000 000 106 mega M
1 000 103 kilo K
100 102 hecto h
10 10 deca da
0.1 10-1 deci d
0.01 10-2 centi c
0.001 10-3 milli m
0.000 001 10-6 micro µ
0.000 000 001 10-9 nano n
0.000 000 000 001 10-12 pico p
R.N.Mutagi EMI June 2016 16

17. Values Scientific
notation
Engineering
notation
Metrix prefix
notation
45 000 000 Hz
0. 000 0047 F
120 000 000 Ω
3 000W
0.01V
0.00001 H
0.000 0012A
0.000 056V
0.000 000 000 07W
R.N.Mutagi EMI June 2016 17

18.  Accuracy: Closeness of the measured value to the actual
value
 Precision: A measure of the reproducibility of
measurement
 Sensitivity: Ratio of the output response of instrument to
the input change
 Resolution: Smallest change in the input to which the
instrument responds
 Error: Deviation from the true (expected) value of
measured parameter
R.N.Mutagi EMI June 2016 18

19. Not Precise,
NotAccurate
R.N.Mutagi EMI June 2016 19
Not Precise
Accurate
Precise
NotAccurate
Precise
Accurate

20.  Error is the degree to which a measurement
conforms to the expected or true value
 Errors are due to measuring instruments (causing
the change in the value of the parameter being
measured) or due to persons carrying out the
measurements (human errors)
 Errors may be expressed as absolute or percentage
R.N.Mutagi EMI June 2016 20

21.  Gross errors
R.N.Mutagi EMI June 2016 21
 Humanerrors
 Systematic errors
 Instrumenterrors
 Environmental errors
 Observational errors
 Random errors

22.  The output voltage of a 5 V DC supply is measured as 4.9 V.
Find (1) Absolute error (2) Percent error (3) Relativeaccuracy
and (4) Percent accuracy
 Solution:
(1) Absolute error = 5 – 4.9 = 0.1V
(2) Percent error = [(5- 4.9)/5]100 = (0.1/5)100 = 2 %
(3) Relative accuracy = 1 – 0.02 = 0.98
(4) Percent accuracy = 0.98 x100 = 98%
R.N.Mutagi EMI June 2016 22

23.  A production batch of resistors of 4.7 kΩ has measured
values ranging from 4.935 kΩ and 4.465 kΩ at 25 0C.
The temperature coefficient of the resistors is 5 ppm/0C
Find: (i) Maximum absolute error, (ii) Maximum relative
error, (iii) Resistor tolerance (iv) Max resistance of a
resistor at 800C (pg 19)
 Answers:
(i) maximum absolute error = + 235 Ω
(ii) maximum relative error = + 5%
(iii) tolerance = + 5%
(iv)
R.N.Mutagi EMI June 2016 23

24.  Indicates the precision of measurement
 A voltmeter with 4 significant figure display has a
precision of 0.001 V
Result Range of Actual value
5 m 4.5 m – 5.5 m
5.0 m 4.95 m – 5.05m
5.00m 4.995m – 5.005 m
5.000 m 4.9995 m – 5.0005 m
4 6R.N.Mutagi EMI June52016 24

25. E V1 V2
 (V1  V1)  (V2  V2 )
 (V1 V2 )  (V1  V2 )
R.N.Mutagi EMI June 2016 25
E  V1V2
Error in the sum of quantities
equal the sum of absolute errors
 (V1  V1)  (V2  V2 )
 (V1 V2 )  (V1  V2 )
Error in the difference of quantities
equal the sum of absolute errors

26. EI
R.N.Mutagi EMI June 2016 26
Percentage error in P is
% error in P  %error in I %error in E

 I E 
I

E
100%
 I. E
100% P 
E.I  
 E.I  E.I  I.E
Percentage error in the product
or quotient of quantities equals
the sum of percentage errors
P  EI  (E  E)(I  I)
 E.I  E.I  I.E E.I
( E.I is verysmall)

27.  When measurements are repeated the results can be
different each time due to errors
 To estimate the deviation from true value and
correctness of the measured value statistical methods
are adopted
 Statistical parameters used are
 Arithmetic mean
 Deviation from the mean
 Average deviation
 Standard deviation
 Variance
R.N.Mutagi EMI June 2016 27

28.  If x1, x2, x3, …., xn are the readings from n
measurements the arithmetic mean is obtained as
x 
x1  x2 x3 .....  xn
n
 Deviation of a reading is the departure of the measured
value from the arithmetic mean
di  xi  x
 Deviation can be positive or negative
R.N.Mutagi EMI June 2016 28

29.  Average deviation D is the arithmetic mean of the absolute
values of the deviations of each of the n measurements. The
algebraic sum of deviations is always zero.
 It indicates the precision of the measuring instrument
 Standard deviation σ is the RMS value of the deviation
 Variance σ2 is the mean square deviation
d
n
D 
1 2 3d 
d  d ..... dn
n
n
R.N.Mutagi EMI June 2016 29
d
n
d 
 d
2
i
2
n3
2 2
2
2
1  d ..... d
 

30. R.N.Mutagi EMI June 2016 30

31. R.N.Mutagi EMI June 2016 31

32. Electric
Input
parameter
Signal
conditioner
Analog/Dig
Converter
Signal
processor
Display
unit
Non-
electric
Input
parameter
Signal
conditioner
A/D
Converter
Signal
processor
Display
unit
Trans
ducer
R.N.Mutagi EMI June 2016 32