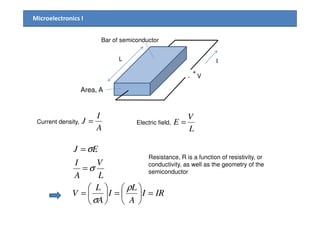
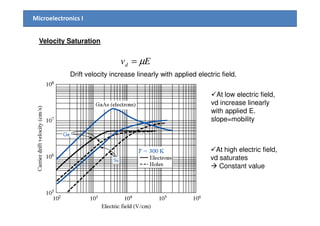
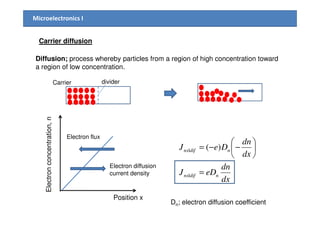
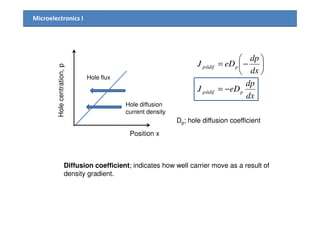
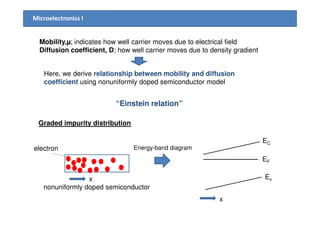
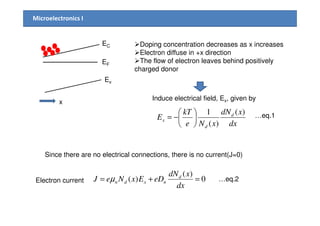
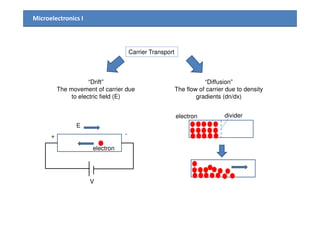
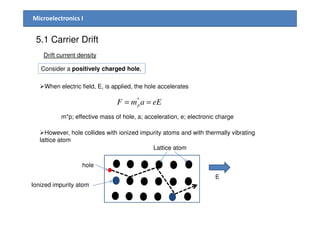
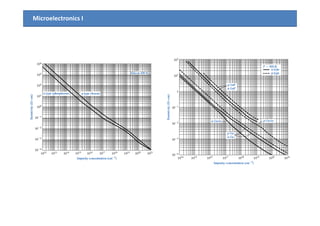
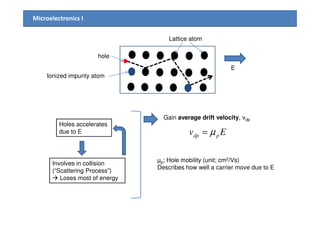
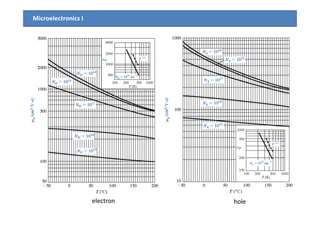
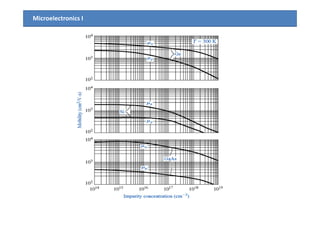
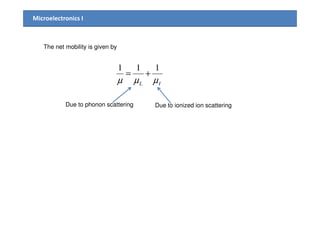
1) The document discusses carrier transport in semiconductors, including drift and diffusion currents. Carrier drift occurs due to an electric field and is characterized by carrier mobility, while diffusion is due to concentration gradients and characterized by the diffusion coefficient. 2) Mobility is affected by phonon and ionized impurity scattering. The net mobility is the sum of these scattering components. Conductivity is directly proportional to carrier concentration and mobility. 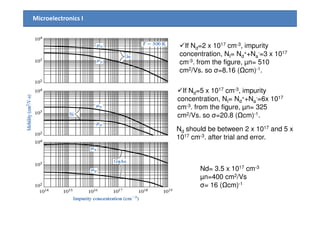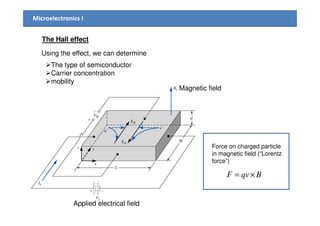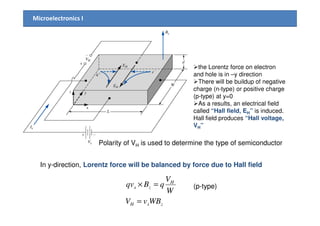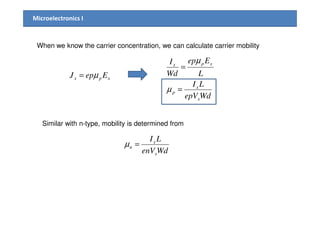3) The Hall effect can be used to determine the type of semiconductor (n-type or p-type), carrier concentration, and carrier mobility. Measurement of the Hall voltage polarity indicates type, and its magnitude relates to concentration and mobility.

1. Microelectronics I
Chapter 5: Carrier Transport
Phenomena
Transport; the process by which charged particles (electrons
and holes) move

2. Microelectronics I
Understanding of electrical properties ( I-V characteristics)
Basic current equation;
EneI ⋅⋅⋅∝ µ
e; electronic charged (constant, 1.6 x 10-19 C)
u; mobility ( figure of merit that reflect the speed)
n; carrier concentration
E; Electric field
Carrier concentration (electron, no and hole, po)
Chapter 4
Carrier transport (current)
This chapter
E; Electric field

3. Microelectronics I
Carrier Transport
“Drift”
The movement of carrier due
to electric field (E)
“Diffusion”
The flow of carrier due to density
gradients (dn/dx)
dividerelectron
V
+ -
E
electron
dividerelectron

4. Microelectronics I
5.1 Carrier Drift
Drift current density
Consider a positively charged hole,
When electric field, E, is applied, the hole accelerates
eEamF p == *
m*p; effective mass of hole, a; acceleration, e; electronic charge
However, hole collides with ionized impurity atoms and with thermally vibrating
lattice atom
hole
Lattice atom
Ionized impurity atom
E

5. Microelectronics I
hole
Lattice atom
Ionized impurity atom
E
Holes accelerates
due to E
Involves in collision
(“Scattering Process”)
Loses most of energy
Gain average drift velocity, vdp
Ev pdp µ=
µp; Hole mobility (unit; cm2/Vs)
Describes how well a carrier move due to E

6. Microelectronics I
Drift current density, Jdrf (unit; A/cm2) due to hole
dpdrfp epvJ =|
pEeJ pdrfp µ=|
Drift current density due to electron
nEeJ ndrfn µ=|
Total drift current;
EpneJ pndrf )( µµ +=
The sum of the individual electron and hole drift current densities

7. Microelectronics I
Mobility effects
*
p
cp
p
m
eτ
µ =
Mobility is important parameter to determine the conductivity of material
*
n
cn
n
m
eτ
µ =
τ; mean time between collisions
If τ=10-15 s, in average, every 10-15 s, carrier involves in collision @ scattering
Two dominant scattering mechanism
1. Phonon or lattice scattering
2. Ionized scattering

8. Microelectronics I
1. Lattice scattering or phonon scattering
At temperature, T > 0 K, atoms randomly vibrate. This thermal vibrations cause a
disruption of the periodic potential function. This resulting in an interaction
between carrier and the vibrating lattice atoms.
Mobility due to lattice scattering, µL
2/3−
∝ Tµ 2/3−
∝ TLµ
As temperature decreases, the probability of a scattering event decreases. Thus,
mobility increases

9. Microelectronics I
electron hole

10. Microelectronics I
2. Ionized Ion scattering
Coulomb interaction between carriers and ionized impurities produces scattering
or collusion. This alter the velocity characteristics of the carriers.
Mobility due to ionized ion scattering, µI
L
N
T 2/3
∝µ
Total ionized impurity concentrationIN Total ionized impurity concentration
If temperature increases, the random thermal velocity of a carrier increases,
reducing the time the carrier spends in the vicinity of the ionized impurity center.
This causes the scattering effect decreases and mobility increases.
If the number of ionized impurity centers increases, then the probability of a
carrier encountering an ionized impurity centers increases, thus reducing
mobility

11. Microelectronics I

12. Microelectronics I
The net mobility is given by
IL µµµ
111
+=
Due to phonon scattering Due to ionized ion scattering

13. Microelectronics I
Conductivity
EEpneJ pndrf σµµ =+= )(
Drift current
σ; conductivity [( .cm)-1]
)( pne pn µµσ +=
electron
hole
Function of electron and hole concentrations and mobolities
Ρ; resistivity [ .cm]
)(
11
pne pn µµσ
ρ
+
==

14. Microelectronics I

15. Microelectronics I
L
+
- V
I
Area, A
Bar of semiconductor
I V
Current density,
A
I
J = Electric field,
L
V
E =
IRI
A
L
I
A
L
V
L
V
A
I
EJ
=





=





=
=
=
ρ
σ
σ
σ
Resistance, R is a function of resistivity, or
conductivity, as well as the geometry of the
semiconductor

16. Microelectronics I
Consider p-type semiconductor with an acceptor doping Na (Nd=0) in which Na>>ni
pepne npn µµµσ ≈+= )(
Assume complete ionization
ρ
µσ
1
≈≈ an Ne
Function of the majority carrier

17. Microelectronics I
ex.;
Consider compensated n-type Silicon at T=300 K with a conductivity of σ=16
( cm)-1 and an acceptor doping concentration of 1017 cm-3. Determine the donor
concentration and the electron mobility.
Solution;
At T=300 K, we can assume complete ionization. (Nd-Na >>ni)
)10()106.1(16
)(
1719
−×=
−=≈
−
dn
adnn
N
NNene
µ
µµσ
To determine µn and Nd, we can use figure mobility vs. impurity concentration with
trial and error
)10(10 1720
−= dn Nµ

18. Microelectronics I
If Nd=2 x 1017 cm-3, impurity
concentration, NI= Nd
++Na
-=3 x 1017
cm-3. from the figure, µn= 510
cm2/Vs. so σ=8.16 ( cm)-1.
If Nd=5 x 1017 cm-3, impurity
concentration, NI= Nd
++Na
-=6x 1017
cm-3. from the figure, µn= 325
cm2/Vs. so σ=20.8 ( cm)-1.cm2/Vs. so σ=20.8 ( cm)-1.
Nd should be between 2 x 1017 and 5 x
1017 cm-3. after trial and error.
Nd= 3.5 x 1017 cm-3
µn=400 cm2/Vs
σ= 16 ( cm)-1

19. Microelectronics I
Ex 2.; designing a semiconductor resistor with a specified resistance to
handle a given current density
A Si semiconductor at T=300 K is initially doped with donors at a concentration of
Nd=5 x 1015 cm-3. Acceptors are to be added to form a compensated p-type
material. The resistor is to have a resistance of 10 k and handle a current
density of 50 A/cm2 when 5 V is applied.
Solution;
When 5 V is applied to 10 k resistor, the current, I
mA
R
V
I 5.0
10
5
4
===
If the current density, J is limited to 50 A/cm2, the cross-sectional area, A is
25
3
10
50
105.0
cm
J
I
A −
−
=
×
==

20. Microelectronics I
Consider that electric field, E is limited to 100 V/cm. Then the length of the
resistor, L is
The conductivity, σ of the semiconductor is
cm
E
V
L 2
105
100
5 −
×===
1
54
2
)(5.0
1010
105 −
−
−
Ω=
×
×
== cm
RA
L
σ
The conductivity of the compensated p-type semiconductor is
)( dapp NNepe −=≈ µµσ
Here, the mobility is function of total ionized impurity concentration Na+Nd

21. Microelectronics I
Using trial and error, if Na=1.25x1016cm-3 , then Na+Nd=1.75x1016cm-3, and the
hole mobility, from figure mobility versus impurity concentration, is approximately
µp=410 cm2/Vs. The conductivity is then,
492.0)10)55.12((410106.1)( 1519
=×−×××=−= −
dap NNeµσ
This is very close to the value we need. From the calculation
L=5x10-2 cm
A=10-5cm2
Na=1.25x1016cm-3

22. Microelectronics I
Velocity Saturation
Evd µ=
Drift velocity increase linearly with applied electric field.
At low electric field,
vd increase linearly
with applied E.with applied E.
slope=mobility
At high electric field,
vd saturates
Constant value

23. Microelectronics I
Carrier diffusion
Diffusion; process whereby particles from a region of high concentration toward
a region of low concentration.
dividerCarrier
Electronconcentration,n
Position x
Electron diffusion
current density
Electron flux
dx
dn
eDJ
dx
dn
DeJ
ndifnx
ndifnx
=






−−=
|
| )(
Dn; electron diffusion coefficient

24. Microelectronics I
Holecentration,p
Hole diffusion
current density
Hole flux
dx
dp
eDJ
dx
dp
eDJ
pdifpx
pdifpx
−=






−=
|
|
Holecentration,p
Position x
current density
Dp; hole diffusion coefficient
Diffusion coefficient; indicates how well carrier move as a result of
density gradient.

25. Microelectronics I
Total Current Density
Total Current
Density
Electron drift
current
hole drift
current
Electron diffusion
current
hole diffusion
current
difpxdrfpdifnxdrfn JJJJJ |||| +++=
dx
dp
eD
dx
dn
eDEepEenJ pnxpxn −++= µµ
1-D
3-D
peDneDEepEenJ pnpn ∇−∇++= µµ

26. Microelectronics I
Mobility,µ; indicates how well carrier moves due to electrical field
Diffusion coefficient, D; how well carrier moves due to density gradient
Here, we derive relationship between mobility and diffusion
coefficient using nonuniformly doped semiconductor model
“Einstein relation”
Graded impurity distribution
nonuniformly doped semiconductor
electron
x
EC
EF
Ev
x
Energy-band diagram

27. Microelectronics I
EC
EF
Ev
x
Doping concentration decreases as x increases
Electron diffuse in +x direction
The flow of electron leaves behind positively
charged donor
Induce electrical field, Ex, given by
xdNkT
E d )(1




−= …eq.1
dx
xdN
xNe
kT
E d
d
x
)(
)(
1






−=
Since there are no electrical connections, there is no current(J=0)
0
)(
)( =+=
dx
xdN
eDExNeJ d
nxdnµ
…eq.1
…eq.2Electron current

28. Microelectronics I
From eq.1 and 2,
e
kTD
n
n
=
µ
Hole current must also be zero. We can show that
e
kTDp
=
µ epµ
e
kTDD
p
p
n
n
==
µµ
Diffusion coefficient and mobility are not independent parameters.
The relationship between this 2 parameter “Einstein relation”

29. Microelectronics I
The Hall effect
Using the effect, we can determine
The type of semiconductor
Carrier concentration
mobility
Magnetic field
Applied electrical field
Force on charged particle
in magnetic field (“Lorentz
force”)
BqvF ×=

30. Microelectronics I
the Lorentz force on electron
and hole is in –y direction
There will be buildup of negative
charge (n-type) or positive charge
(p-type) at y=0
As a results, an electrical field
called “Hall field, EH” is induced.called “Hall field, EH” is induced.
Hall field produces “Hall voltage,
VH”
In y-direction, Lorentz force will be balanced by force due to Hall field
zxH
H
zx
WBvV
W
V
qBqv
=
=× (p-type)
Polarity of VH is used to determine the type of semiconductor

31. Microelectronics I
For p-type
))(( Wdep
I
v x
x =
deV
BI
p
epd
BI
V
H
zx
zx
H
=
=
Can calculate the hole concentration in p-type
deVH
For n-type
deV
BI
n
end
BI
V
H
zx
zx
H
−=
−=
Note that VH is negative for n-type

32. Microelectronics I
When we know the carrier concentration, we can calculate carrier mobility
xpx EepJ µ=
WdepV
LI
L
Eep
Wd
I
x
x
p
xpx
=
=
µ
µ
Similar with n-type, mobility is determined from
WdenV
LI
x
x
n =µ