This document discusses voltage regulation and summarizes the key characteristics and equations for various voltage regulation devices: 1. Step-type voltage regulators, load tap changing transformers, and shunt capacitors are common methods for regulating voltage. 2. It provides the generalized constants (a, b, c, d) that model single-phase transformers, auto-transformers, and voltage regulators as two-port networks. These constants allow modeling the input-output voltage and current relationships. 3. It summarizes the characteristics of step voltage regulators, including the differences between Type A and Type B regulators. Type B regulators are more common and have constant core excitation since the shunt winding is connected to the control circuit. The

1. D

2. Distribution Voltage Regulation
The voltage at every customer’s service
entrance must remain within acceptable
tolerances. Common methods of regulating
the voltage are:
1. Step- type voltage regulators
2. Load tap changing transformers and
3. Shunt Capacitors.

3. Two Winding Transformer Theory
Standard Markings: High Voltage Side: H1, H2
Low Voltage Side: X1, X2
s.t. (a) at no load, Vs is in phase with VL
(b) under s.s. load conditions I1 in phase with I2

4. Referring the leakage impedance to the secondary, we have:
The total leakage impedance is now given by:
Zt = nt2 Z1 + Z2 … (1)
where nt = N2/N1
For an ideal transformer:
E2 = N2/N1E1 = ntE1 … (2)
I1 = N2/N1I2 = ntI2 … (3)
Applying KVL to the secondary:
E2 = VL + I2Zt … (4)
But VS = E1 = 1 E2 = 1 VL + Zt I2 … (5)

5. Equation (5) can be written as:
VS = a.VL + b.I2 … (6)
where a = 1 and … (7)
nt
b = Zt … (8)
nt
Also, IS = Ym.VS + I1 … (9)
Sub (3) and (5) into (9)
IS = Ym. 1 [ VL + ZtI2 ] + nt.I2
nt
IS = Ym VL + [ YmZt + nt ] I2 … (10)
nt nt
In general form, (10) can be rewritten as
IS = c. VL + d. I2 … (11)
where c = Ym … (12)
nt
d = Y .Z + n … (13)

6. We now have a model of a 1Φ transformer as a two port device:
i.e.:
VS = a.VL + b. I2 … (6)
IS = c. VL + d. I2 … (11)
where the a, b, c, d constants are:
a=1 ; c = Ym
nt nt
b = Zt ; d = Ym.Zt + nt
nt nt
If the O/P voltage is needed, then (6) can be rewritten as:
VL = 1/a VS – b/a I2 … (14)
Sub. for a and b in (14) we get
VL = AVS – BI2 … (15)
where A = 1/a = nt … (16)
∴ B = b/a = Zt … (17)
VL = ntVS – ZtI2

7. Example:
A 1Φ transformer is rated 75kVA 2400/240 V. The
transformer has the following impedances and shunt
admittances:
Z1 = (0.612 + j1.2) Ω (HV)
Z2 = (0.0061 + j0.0115) Ω (LV)
Ym = (1.92x10-4 – j8.52x10-4) s (referred to HV side)
Determine the generalized a, b, c, d constants as well as
the A and B constants for the transformer. What should
be the primary Voltage and Current at rated kVA and 0.9
p.f. lag.

8. Solution:
Nt = N2 = 240 = 0.1
N1 2400
Equivalent impedance of transformer referred to L.V.
Zt = Z2 + nt2.Z1 = 0.0122 + j0.0235
The generalized constants are:
a = 1/nt = 10 ; b = Zt/nt = 0.122 + j0.235
c = Ym/nt = 0.0019 – j0.0085
d = Ym.Zt + nt = 0.1002 – j0.0001
nt
A = nt = 0.1 ; B = Zt = 0.0122 + j0.0235
VL = 240 ∠ 0
Assuming that transformer operating at 75kVA, 240 V 0.9 lag (Rated)
I2 = 75 x 1000 ∠ -25.84 = 312.5 ∠-25.84
240
VS = aVL + bI2 = 2466.9 ∠ 1.15 V
Applying the values of a, b, c and d parameters:
IS = cVL + dI2 = 32.67 ∠ -28.75 A

9. Two Winding Auto-Transformer (Buck/
Boost Transformer)
• The two winding transformer can be
connected as an autotransformer.
STEP
UP
• This is done by connecting X2 to H1 and
taking the output from X1H2 for step up.
STEP
DOWN • Connect X1 to H1 and output is X2H2.
• LV winding is referred to as the “series”
winding and the HV winding as the “shunt”
winding (in relation to the Load).

10. STEP- UP AUTO TRANSFORMER

11. In this case, the total equivalent impedance is referred to the “series”
winding.
(Boost Transformer) Applying KVL to secondary circuit:
E1 + E2 = VL + Zt.I2 … (1)
Or E1 + ntE1 = (1 +nt)E1 = VL + Zt.I2 … (2)
From the circuit: VS = E1 and I2 = IL … (3)
Sub (3) into (2)
VS = 1 VL + Zt . I L … (4)
1+nt 1+nt
Or VS = a’.VL + b’.IL … (5)
where a’ = 1 and b’ = Zt
1+nt 1+nt
Applying KCL to node X2
IS = I1 + I2 + Iex … (7)
IS = (1+nt)I2 + Iex
= (1+nt)I2 + YmVs … (8)

12. Sub (4) into (8) gives:
 1 Zt 
I S = (1 + nt ).I 2 + Ym  .VL + .I 2 
1 + nt 1 + nt 
Ym  Ym .Z t 
I S= .VL +  + 1 + nt  I 2 … (9)
(1 + nt )  1 + nt 
But I2 = IL
Or IS = c’.VL + d’.IL … (10)
where c’ = Ym and d’ = YmZt +1 + nt … (11)
(1+nt) (1+nt)

13. Step Down Auto-Transformer
(X1 connected to H1)
In this case for KVL => E1- E2 = VL + I2Zt

14. If the analysis is continued as before we get;
VS = aVL + bIL … (12)
IS = cVL + dIL … (13)
}
where a = 1 b = Zt
1-nt 1-nt (14)
c = Ym d = YmZt + 1 –nt
∴ 1-nt 1-nt
[ the only difference is the sign of the turns ratio.]
∴
Generalized Constants for Auto-Transformer can be defined as:
a= 1
1±nt
c = Ym
1±nt
b = Zt
1±nt
d = YmZt + 1 ± nt
1±nt
} (15)
From (12) VL = 1/a.VS – b/a.IL ... (16)
Or VL = A.VS – BIL
where A = 1/a = 1±n ; B = b/a = Z … (17)

15. The generalized equations for the auto-
transformer are of exactly the same form as
was derived for the two winding transformer
as well as for a transmission line. (In terms of
a, b, c, d constants). These single phase
values will be expanded to a 3x3 matrix for
the 3Φ transformer.

16. Rating of Autotransformer
The rating is given by: VSIS or VLIL
Let: kVAxfm = kVA rating of two winding transformer
kVAauto = kVA “ “ autotransformer
Vrated1 = E1 = rated source voltage
Vrated1 = E2 = rated load voltage
Vauto S = rated source voltage of autotransformer
Vauto L = rated load voltage autotransformer
Neglecting voltage drop across Zt
Vauto L = E1 ± E2 = (1 ± nt)E1 … (18)

17. ∴ kVAauto = Vauto L . I2 = (1 ± nt)E1I2 … (19)
But I1 = ntI2
∴ kVAauto = (1 ± nt) . E1. I1 … (20)
nt
But E1I1 = kVAxfm
∴
kVAauto = (1 ± nt) kVAxfm … (21)
nt
Fundamental Equations for Buck/Boost transformer:
(1) Vauto L = (1 ± nt) E1
kVAauto = (1 ± nt) kVAxfm
nt
where nt = N2
N1
Example:
The 75kVA 2400/240V transformer given before is connected as a step-up auto
transformer.
1.Determine the kVA rating and voltage output of this arrangement.
2.If the auto transformer is supplying rated kVA at rated voltage at 0.9 lag,
determine source voltage and current.

18. nt = 0.1 ; kVAxfm = 75 2400/240
∴
1. ∴ kVAauto = ( + 0.1 ) 75 = 825 kVA
1
0.1
V1 = VS = 2400
Vauto L = (1 + n) E1
= (1.1)(2400) = 2640 V
= (V1 + V2) = (2400 + 240)
= 2640V

19. (2) VL = 2640 ∠0 V
I2 = 825 x 103 ∠ -25.84 = 312.5 ∠ -25.84 A
2640 /0
∴ a = 1/(1+0.1) = 0.9091
b = 0.0122 + j0.0235 = (0.0111 + j0.0214)
1 + 0.1
∴ c = (1.92 – j8.52) x 10-4 = (1.7364 – j7.7455) x 10-4
1 + 0.1
∴ [ ]
d = (1.92 – j8.52)(0.0122 + j0.0235) x 10-4 + 1 + 0.1
1 + 0.1
= (1.1002 – j0.000005)

20. But VS = aVL + bIL
IS = cVL + dIL
VS = (a)2560 ∠ 0 + b(312.5 ∠ -25.84)
Sub for a, b, c and d we get:
= 2406 ∠ 0.1 V
IS = (c)(2640 ∠ 0) + d(312.5 ∠ -25.84)
= 345.06 ∠ -26.11
Check VL = AV –BIL
where A = 1 + nt = 1.1
B = Zt = 0.0111 + j0.0235
VL = (1.1)(2406 ∠ 0.1) – (0.0111 + j0.0235)(312.5 ∠ -25.84)
= 2640 ∠ 0

21. Step Voltage Regulators
1. A step voltage regulator consists of an auto
transformer and a load tap changing mechanism.
2. Voltage changes obtained by changing taps in series
winding.
3. The position of tap controlled by a control unit
called the line drop compensator.
4. Regulator has a reversing switch enabling a ± 10%
regulating range typically in 32 steps.
5. On a 120V basis this yields 0.75V per step.
6. As per ANSI/IEEE C57-1986 standard there are two
types: Type A and Type B. (Type B more common)

22. CONTROL SETTINGS
a.Voltage Level -: Voltage to be maintained.
b.Bandwidth -: Deadband.
If (a) = 122V and Bandwidth = 2V then voltage is
between 121-123.
c.Time Delay -: Wait time before execution of a tap
change.
d.Line Drop Compensator -: Used to compensate for Vdrop
due to line impedance.

23. TYPE B Step- Voltage Regulator

24. TYPE A Regulator

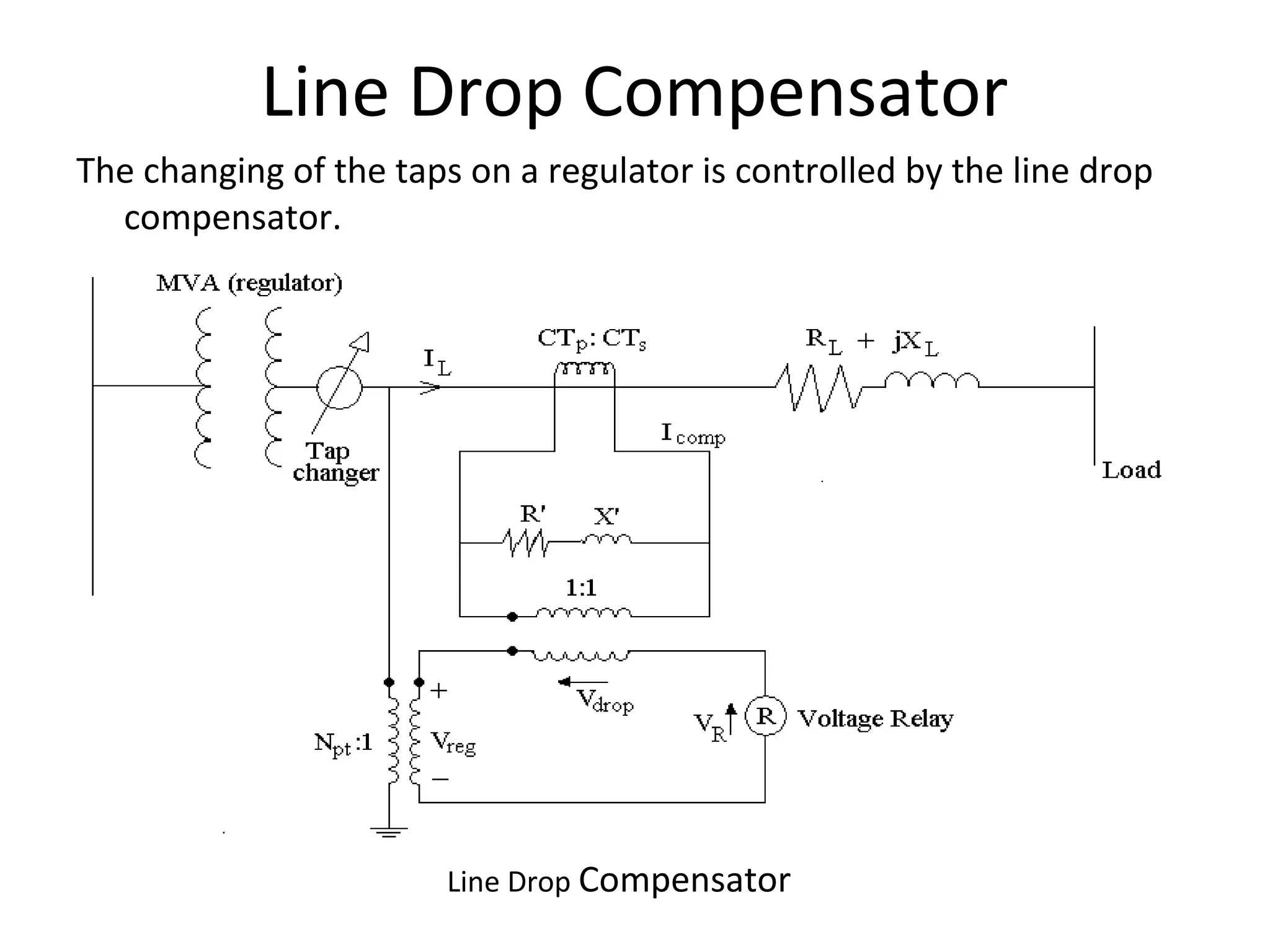
25. Note: In type B regulator, the core excitation is constant because the
shunt winding is connected to the control circuit i.e. the
regulated line drop compensator.
Diagram gives Regulator in Raise (step up) connection (R). For Lower (L) (step
down) the switch is moved to ‘L’.
Voltage Equations Current Equations
E1 = E2 N1I1 = N2I2 … (1)
N1 N2
VS = E1 – E2 IL = IS – I1 … (2)
VL = E1 I2 = IS … (3)
E2 = N2 E1 = N2 VL I1 = N2 I2 = N2 IS … (4)
N1 N1 N1 N1
VS = [1 – N ]V
2 L [
IL = 1 – N2 ]I s … (5)
N1 N1
VS = ar . VL where ar = 1 – N2 IL = ar . IS … (6) … (7)
( N1
)

26. When the switch is placed on L (Lower or step down) only equation (2)
changes -: VS = E1 + E2 ; IL = IS + I1
This again gives equation (6) but in this case
a r = 1 + N2 … (8)
N1
If N2/N1 is not known but we know the tap change is 0.75V.
∴Effective regulator ratio for type B regulator:
On 120V ; 0.75V = 0.00625 p.u.
∴ effective ratio = ar = 1 ± (0.00625)(# tap) … (9)
where: - = raise
+ = lower

27. Generalized Constants (a, b, c, d)
For Type A and Type B regulators we have:
Type A: VS = 1 VL ; IS = arIL
ar
Type B: VS = arVL ; IS = 1 IL
ar
Effective ratio
}
with Type A Type B For
equation
raise + - (9)
lower - +

28. ∴Generalized Constants for 1Φ step-voltage regulator are:
Type A: a = 1/ar b=0 c=0 d = ar … (10)
Type B: a = ar b=0 c=0 d = 1/ ar … (11)
where ar is given by (9) with sign given by table before.

29. Line Drop Compensator
The changing of the taps on a regulator is controlled by the line drop
compensator.
Line Drop Compensator

30. a) The current transformer ratio is specified as CTp:CTs where the
primary rating (CTp) is typically the rated current for the circuit
(or feeder).
b) The compensator is an analog circuit i.e. it is a scale model
(R’ + jX’) of the line impedance (RL + jXL).
(R’ + jX’ -: scale model; replica impedance; analog of the line)
c) R’ + jX’ is calibrated in volts
d) ZL pu = Zcomp pu

31. Table of Base Values
Base Line Cct Compensator Cct
Voltage VLN VLN/Npt
Current CTp CTs
Zbase VLN/CTp VLN/( Npt . CTs)
From this we can derive R’ & X’ (Compensator)
Rpu + jXpu = RL + jXL
Zbline
∴ R + jX = (R + jX ) CT … (1)
pu pu L L p
VLN
For the compensator to function, ZL pu = Zcomp pu.
∴
(Rcomp + jXcomp)Ω = (Rpu + jXpu)Zbase comp
∴
(Rcomp + jXcomp)Ω = (RL + jXL) CTp . VLN
VLN (Npt . CTs)
Or (Rcomp + jXcomp)Ω = (RL + jXL) CTp . 1 … (2)

32. Equation (2) gives the ohmic value of the compensator.
To obtain the R and X settings in Volt we multiply the ohmic value by
the rated current:
(R’ + jX’) volt = (Rcomp + jXcomp). CTs
(R’ + jX’) volt = (RL + jXL) CTp. CTs
Npt. CTs
∴ (R’ + jX’) volt = (R + jX ) CT volt … (3)
L L p
Npt
Example:
For the compensator circuit given before, the regulator (transformer)
rated 5000kVA, 115 delta- 4.16kV grounded wye and the equivalent
line impedance from the Regulator to the load centre is (0.3 + j0.9)Ω.
a) Determine the VT and CT ratings for the compensator cct.
b) Determine the R and X setting of the compensator in Ω and volts.

33. Solution:
a) VLG = 4160/ √3 = 2401.8 V.
For a 120V compensator operation (Normal voltage)
Npt = 2401.8 ≈ 20
120
Rated current of Regulator = 5000 = 693.9 A
√3. x 4.16
∴ Select primary rating of CT as 700A
Assuming compensator secondary = 5A
 CT = CTp = 700 = 140
CTs 5
b) (R’ + jX’) volts = (RL + jXL) CTp
Npt
= (0.3 + j0.9) 700 /20 = (10.5 + j31.5) V
The R and X setting in Ω is obtained by dividing the volt settings by CTs
(current rating)
(RΩ +jXΩ) compensator = (10.5 + j31.5)/5
= (2.1 + j6.3) Ω
Remember that the compensator is set in volts i.e. at (10.5 + j31.5) V.

34. Example:
Assume the regulator is supplying 2500kVA at 4.16kV, 0.9 p.f. lag. If the voltage
level at the load centre is to be 120V of bandwidth 2V, determine the tap
setting of the regulator.
Solution:
As calculated before:
Setting of regulator = R’ + jX’ = (10.5 + j31.5) V
∴ IL = 2500 ∠ -25.84 = 346.97 ∠-25.84 A
VL = 120 ± 1
∴ Icomp = 346.97 ∠ θ = 2.4783 ∠ -25.84 A
√3 x 4.16
Input voltage to regulator = 4160 ∠ 0 = 120.09 ∠ 0
140
√3 x 20
Vdrop = (2.1 + j6.3)(2.4783 ∠-25.84) = 16.458 ∠ 45.72 V
Voltage drop in compensator cct = (Zcomp)Ω (Icomp).
∴
VR = Vreg – Vdrop = (120.09 ∠ 0) – (Vdrop)
Voltage across compensator relay = VR
∴

35. NB:
VR represents the voltage expected at the load centre due to the
voltage drop across the line (RL + jXL)
The min. value for this voltage should be 119V.
∴ the regulator has to raise Taps.
Recall for a typical regulator, on tap ≡ 0.75V
∴ # of taps required = 119 – 109.24 = 13.02
0.75
∴ for a Type B regulator in raise position the effective ratio is:
ar = 1 - (0.00625)(# of taps)
= 1 – (0.00625)(13) (for Type B “raise”)
= 0.9188
∴ the generalized constants for modeling this regulator for
this operating condition are:
a = ar = 0.9188 c=0
b=0 d = 1/ar = 1.0884

36. Example Continued:
For the system given before, calculated the actual voltage at the load centre
assuming that 2500kVA at 4160 is measured at the substation transformer low-
voltage terminals.
Solution:
∴ VL = (4160 0 /√3) 1/0.9188 = 2614.2 ∠ 0 V
Recall VL = VS / ar ; IL = arIS
IL = arIS = (0.9188)(346.97 ∠-25.84)
= 318.77 ∠ -25.84 A
Also
∴
Actual voltage at load centre is:
= (2614.2 ∠ 0) – (0.3 + j0.9)(318.77 ∠ -25.84)
VLC = VL – ZLIL
= 2412.8 ∠ -5.15 V
VLC 120 = VLC = 2412.8 ∠ -5.15 = 120.6 ∠ -5.15
On a base 120Vbase, load centre voltage is:
∴ Npt 20
the +13 tap has produced the result needed.
VL = 2614.2 ∠ 0 and IL = 318.77 ∠ -25.84
** Recheck with the previous example for
Find V .

37. Three Phase Step Voltage Regulators
Three 1Φ step-voltage regulators can be
connected externally to form a 3Φ regulator.
 In this case each regulator has its own
compensator circuit and can be tapped
independently.
Normally only one compensator regulator is
used and the tapping on all 3 phases is
ganged.
In this case, it is left to the engineer to decide
the phase to sample.

38. Wye Connected Regulator (Type B)
Regulator shown in “Raise” Position

39. Voltage Equations
VAN  aRa 0 0  Van 
V  =  0 … (1)
 BN   aRb 0  Vbn 
 
VCN   0
   0 aRc  Vcn 
 
where aRabc = effective turns ratio of the 3 single phase regulators.
Normally aRa = aRb = aRc
We can rewrite (1) in matrix format
[VLN ABC ] = [a].[V ] + [b].[ I ]
LN abc abc … (2)
Also the current equations become:
1 
 0 0 
I a
 A   Ra  Ia 

  0 1
I =
B   0  I b  … (3)

 
a Rb 
C    
I
 
0 1  Ic 


0

 a Rc 

OR
[ I ABC ] = [c].[VLG abc
] + [d ][ I ]
abc … (4)

40. Where:
aRa 0 0 
[a] =  0
 aRb 0  
 0
 0 a Rc 

[b] =[c ] =[0]
 1 
 0 0 
 a Ra 
1
[d ] =  0

0 

a Rb
 1 
 0 0 

 a Rc 

For the typical 120 V base regulator with 0.75V / step:
0.9 ≤ aRabc ≤ 1.1 in 32 steps