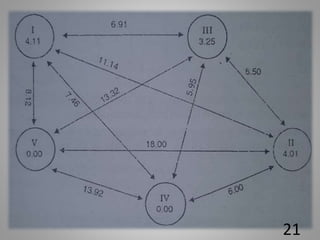
The document discusses the D-square statistic, a measure of group distance based on multiple characteristics, introduced by P.C. Mahalanobis in 1928 and utilized for assessing genetic diversity in plant breeding. It outlines the theory, evaluation of genotypes, biometrical analysis methods, and procedures for grouping genotypes into clusters based on D2 values, including calculations of intra and inter-cluster distances. The document concludes with the importance of individual character contributions to total divergence and references related literature.

1. 1

2. Topic :
D-Square statistic
Name :
M.Zulqarnain
Ali Abbas
2

3. Outline:
D-Square Statistic
Theory of D2 Statistics
Evaluation of Genotypes
Biometrical Analysis
Conclusion
References
3

4. A measure of group distance based on
multiple charaters.
It introduce by P.C.Mahalanobis in 1928.
Rao 1952 use this technique for
assessment of genetic diversity in plant
breeding.
D2 Statistics
4

5. Theory of D2 Statistics
Let us assume:
x1 ,x2 ,x3 ….xp :
are the multiple measurements
on each individual.
d1, d2, d3 ….dp :
are the difference between the
mean of two population for multiple
characters.
5

6. Evaluation of Genotypes:
The genotypes for study of genetic
diversity includes germplasm lines, and
varieties.
Biometrical Analysis:
1. Test of Significance
2. Estimation of D2 Values
6

7. 3.Grouping of genotypes into clusters
4.Average Intra and Inter-cluster Distance
5.Cluster Diagram
6.Contributation of individual characters
towards total divergence
7

8. 1. Test of Significance:
Using this method, the determinant
error+genotype matrices are worked out.
|w| Determinant for error matrix = multiply
all pivotal condensation elements in error
matrix.
|s| Determinant for error + genotype matrix
8

9. = Multiply all pivotal condensation
elements in error matrix + genotype
matrix
Than,=|w|/|s|
2. Estimation of D2 Values:
Estimation of D2 Values by the
formula i.e.
D2=Wij (xi
-1 –xi
-2) (xj
-1 –xj
-2)
9

10. wij is the inverse of variance
and co-variance matrix.
Is very complicated since it
need inversion of matrix of high
order when the of characters
are large.
10

11. Transformation of correlated variables:
This method supplies the values required or
transformation of the raw data.
It is only for variance and covariance matrix is
used.
Computation of D2 values and their significance:
For each combination, the mean deviation i.e.
Yi
1 – Yi
2 is computed and the D2 value is
computed as sum of squares of these
deviations.
D2 = Σ(Yi
1 – Yi
2)
11

12. CONTI…….,
where,
i =1,2,……..p-number of characters
Yi
1=Transformed uncorrelated mean of ith
character for genotype 1
Yi
2 =Transformed uncorrelated mean of ith
character for genotype 2
12

13. oThe significance of D2 values is
tested against the table value of X2
at p degree of freedom, where,
op is the total number of character
included in the study.
Their Significance:
13

14. oIf the calculated the D2 value
is higher than the table X2
value.
oIt is considered as significant.
14

15. The first step in grouping the
genotypes into distinct clusters is to
arrange the genotypes in ordered of
their relatives distance (D2 values)
from each other.
3.Grouping of genotypes into clusters:
15

16.  In this method the two genotypes
having smallest distance from each
other considered first. This is name
as cluster 1.
A second Cluster may be formed in
a similar way. Thus the process is
continue till all the genotypes are
included into one or other cluster.
16

17. 4.Average Intra and Inter-Cluster Distances
• The formula for the measure of average
intra cluster distance is (ΣD2
i /n).
• Where ΣD2
i in the sum of distances
between all possible combinations(n) of
genotype included in a clusters .
17

18.  The inter cluster distance is first
to measure the distance between
various combinations of cluster and
divide by the product of number of
genotypes in the concerned cluster
combinations.
 Average inter cluster distance
between cluster i and j = ΣDi
2 /nixnj
18

19. Where ,
 ΣDi
2 is the some of distance
between the genotypes in cluster i
and j.
 ni =number of genotypes in cluster i
 nj= number of genotypes in cluster j
19

20. With the help of D2 values
between (inter-cluster distance) and
within (intra-cluster distance )
clusters.
A diagram showing the
relationship between different
genotypes be drawn.
Such a diagram is not exactly to
the scale.
5.Cluster Diagram:
20

21. 21

22. 6.Contributation of individual
charaters towards total divergence:
In all combination of genotypes, [n(n-1)/2],
each character is ranked on basic of values
(Yi
1 –Yi
2 ).
Rank 1 is given to the highest mean
difference and rank p to the lowest mean
difference, where p is the total number of
character.
22

23. Percent
contributation
by Xi
No. of times appearing
=first in ranking by X1 x100
[n(n-1)/2]
Xi….Xp are individual character
n is the no. of genotypes
23

24. Reference:
Quantitative Genetics and biometrical
techniques in plant breeding
Writer: Lt.M.Gunasekaran
N.Nadarajan
24

25. 25

26. 26