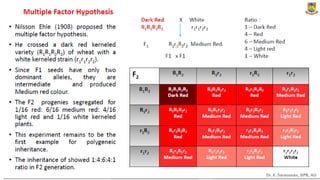
This document provides an introduction to principles of quantitative genetics. It discusses the history and development of the field, beginning with Mendel's foundational work in genetics and Galton's development of statistical techniques. It describes how early geneticists differed in their views of inheritance as qualitative vs quantitative. Key figures who helped establish quantitative genetics are mentioned, including Fisher who integrated Mendelian and statistical approaches. The document outlines differences between Mendelian and polygenic traits. It also discusses types of statistics used in quantitative genetics like first and second degree statistics, as well as biometrical techniques and parameters used in plant breeding like assessment of variability, selection of elite genotypes, choice of parents, and stability analysis.

1. Principles of Quantitative Genetics - Introduction
GPB 621 – PRINCIPLES OF QUANTITATIVE GENETICS
Class - 1
Dr. K. SARAVANAN
Professor
Department of Genetics and Plant Breeding
Faculty of Agriculture
Annamalai University

2. Dr. K. Saravanan, GPB, AU
• Statistics
• Biometrics
• Biometrical Genetics / Quantitative Genetics
.

3. Dr. K. Saravanan, GPB, AU
History of Quantitative Genetics
• Mendel laid the foundation of the genetics.
• Mendel observed seven clear cut visible traits in garden pea (Pisum sativum) and
postulated laws of inheritance of characters.
• The mathematical foundations for the study of quantitative variation
were first laid by Galton (1989).
• He studied the physical and mental characteristics of human beings. He observed
that taller individuals, produced taller children on an average. To measure the degree
to which such characteristics were inherited, new biometical techniques such as
correlation and regression were developed by Galton and his students.
• In 1900 Mendel’s work was rediscovered.
• Different views formed the basis for the two main groups among geneticists, namely
“Mendelians” who proposed that heritable characters were qualitative and
discontinuous (discrete) in distribution and “biometricians” who believed that the
heritable variation was basically quantitative and continuous in distribution.
.

4. Dr. K. Saravanan, GPB, AU
• Yule (1906) –
• consider both groups and give suggested that there need be no conflict
between particulate inheritance and continuous inheritance if many genes
having small and similar effects were postulated.
• Johannsen (1909)
• In demonstrating the occurrence of quantitative genetic variation, stated that
both heritable and non heritable factors were responsible for variations
observed in the seed weight of beans (Phaseolus vulgaris).
• P = G + E
• Nilson-Ehle (1909) – Multiple factor hypothesis was proposed.
• Devanport (1913)
• Analysed the skin colour inheritance in the progeny of Negro-White mating
and concluded that the hypothesis of multiple factors explains the inheritance
of skin colour in Mulattoes.
.

5. Dr. K. Saravanan, GPB, AU
• East (1916)
• Conclusive evidence for the hypothesis that several genes with small, similar and
additive effects govern the inheritance of quantitative characters was provided by
E.M.East in 1916. East began his studies with two true breeding varieties of tobacco
(Nicotiana longiflora) that differed in respect of flower length.
• Fisher (1918)
• Showed how the biometrical findings could be interpreted in terms of Mendel’s
factors.
• He showed how statistically the effect of environment can be partitioned form
genetic effects.
• He provided the initial frame of biometrics for the study of quantitative genetics.
• He also partitioned the genetic variance to additive, dominance and epistatic
components.
• In so bringing together the Galton approach and the Mendelian basis, Fisher laid the
foundation for quantitative genetics.
.

6. Dr. K. Saravanan, GPB, AU
Mendelian Vs Polygenic Traits
.
Mendelian Genetics Biometrical Genetics
1. Governed by Oligogenes Governed by Polygenes
2. The variation is discontinuous The variation is continuous
3. The individuals can be grouped into distinct
classes
The individuals can not be grouped into distinct
classes
4. The expression of the character is least
influenced by the environment
The expression of the character is highly
influenced by environment
5. The inheritance can be studied by grouping
the individuals in to distinct Mendelian
ratios. (Based on frequencies and ratios).
Since the individuals can not be grouped into
distinct ratios, the inheritance can be studied by
statistical quantities like mean, variance and co-
varieance.

7. Dr. K. Saravanan, GPB, AU
Features of Polygenes
1. The variation due to polygenes is continuous between two extremes
2. Quantitative variation is governed by Several Genes
3. The effect of each gene is small or minor but the effect is cumulative
4. Classification of quantitative characters into discrete groups is not
possible
5. Quantitative characters are influenced by environment
6. The effect due to polygenes is qualitative i.e., measurable
7. Quantitative traits exhibit transgressive segregation
8. Polygenes are stable in their inheritance
9. Polygenes exhibit low heritability
.

8. Dr. K. Saravanan, GPB, AU
Types of Statistics : (Mather and Jinks, 1971)
• First degree
• Second degree
• Third degree
(The major part of biometrical analysis is based on first and second degree statistics.)
First degree:
• It is also known as first order statistics.
• It includes mean, which is used for the measurement of all types of parameters.
• The calculation of first order statistics is simple and reliable.
• It is used to study of
• Generation mean
• Heterosis
• Inbreeding depression,
• Metroglyph analysis
• Stability analysis
.

9. Dr. K. Saravanan, GPB, AU
Second degree:
• It is also known as second order statistics.
• It includes estimates of variance and co variances
• The calculation of second order statistics is more difficult than first order
statistics.
• It is used to estimation of
• Correlation
• Path analysis
• Discriminant function
• D2 Statistics
• Heritability
• Genetic advance
• Components of variance in diallele, Partial diallele, L x T, Triple test cross and
biparental crosses.
.

10. Dr. K. Saravanan, GPB, AU
Third degree:
• It is also known as third order statistics or higher order statistics.
• It includes complex interaction like kurtosis and skewness
.

11. Dr. K. Saravanan, GPB, AU
• The various statistical procedures which are employed in the
biometrical genetics are called biometrical techniques.
• In plant breeding
1. Assessment of variability
2. Selection of elite genotypes
3. Choice of suitable parents and breeding procedures
4. Assessment of stability of genotypes.
.
BIOMETRICAL TECHNIQUES AND STATISTICAL PARAMETERS IN PLANT BREEDING

12. Dr. K. Saravanan, GPB, AU
1. Assessment of variability
.
Biometrical techniques Genetic information obtained about
1. Simple measures of variability viz., range, SD, CV,
Variance etc.,
Phenotypic variability
2. Components of genetic variance Genetic variability
3. D2 statistics Genetic diversity
4. Meteroglyph analysis Variability and diversity
2. Selection of elite genotypes
Biometrical techniques Genetic information obtained about
1. Correlation analysis Character association
2. Path analysis Cause and effects
3. Discriminant function Selection criteria

13. Dr. K. Saravanan, GPB, AU
3. Choice of suitable parents and breeding procedures
.
Biometrical techniques Genetic information obtained about
1. Diallel cross analysis gca, sca variance and effects and D & H
2. Partial diallel analysis All above estimates except sca effects
3. L x T analysis gca, sca variance and effects and D & H
4. Biparental Mating Additive and dominance variance
5. Triple Test cross Analysis D, H and presence or absence of epistasis
6. Generation Mean Analysis Additive, dominance and epistatic variance
4. Assessment of stability of genotypes
Biometrical techniques Genetic information obtained about
1. Various stability models Phenotypic stability

14. Dr. K. Saravanan, GPB, AU
.

15. Dr. K. Saravanan, GPB, AU
.

16. Dr. K. Saravanan, GPB, AU
Multiple factor inheritance :
Problem 1.
Assume that two pairs of genes with two alleles each determine plant height
additively in a population. The homozygoes AABB and aabb have 50 cm and 30
cm height respectively.
a). What is the height of F1 in a cross between these two homozygous plants.
b). After F1 x F1 cross, which genotypes in F2 will show a height of 40 cm.
c). What will be the F2 frequency of these 40 cm plants.
.

17. Dr. K. Saravanan, GPB, AU
.

18. Dr. K. Saravanan, GPB, AU
.

19. Dr. K. Saravanan, GPB, AU
Problem 2.
Three independently segregating genes each with 2 alleles determine height in a
particular plant. The presence of each contributing allele adds 2 cm to he base
height of 2 cm.
a). Give the height expected in F1 progeny of a cross between dominant homozygote and
recessive homozygote.
b). Give the distribution of height expected in a F1 x F1 cross.
c). What proportion of this F2 progeny would have heights equal to the parental stocks.
d). What proportion of F2 would breed true for the height shown by F1.
.

20. Dr. K. Saravanan, GPB, AU
.

21. Thank q
Dr. K. Saravanan, GPB, AU