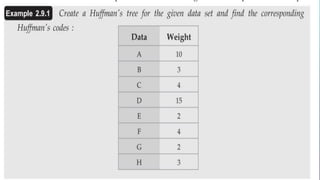
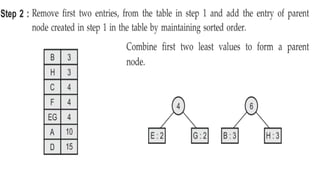
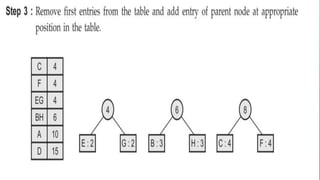
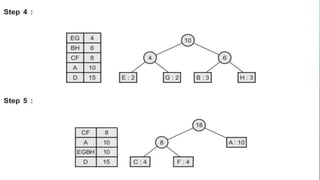
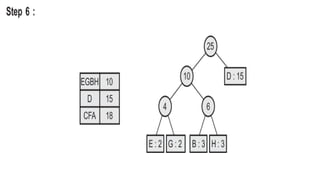
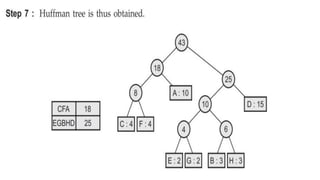
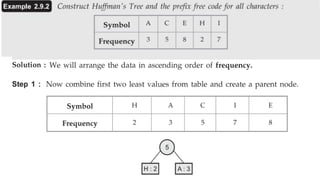
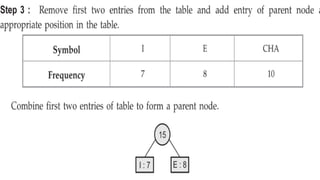
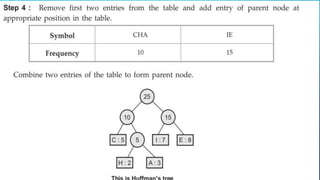
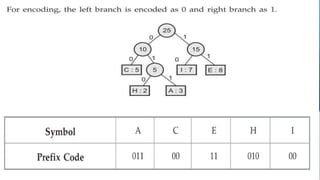
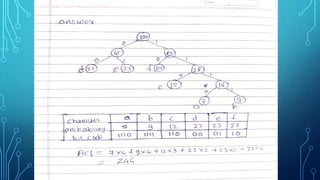
This document provides an overview of Huffman coding and Huffman's algorithm. It discusses how Huffman coding works by assigning variable length binary codes to characters based on their frequency, with more common characters getting shorter codes. It then explains Huffman's algorithm, which builds the Huffman tree by recursively combining the two least frequent nodes until a full binary tree is constructed, and codes are assigned based on paths in the tree. Examples of its applications in data compression are also given.

1. WELCOME
HUFFMAN’S ALGORITHM
AND CODING TREE
Presented by :
Pawar Ganesh Dattatraya
Pawar Tushar Bariknath

2. HUFFMAN CODING TREE
• Huffman Coding is a technique of compressing
data to reduce its size without losing any of the
details. It was first developed by David
Huffman.
• Huffman Coding is generally useful to compress
the data in which there are frequently
occurring characters.

3. HUFFMAN CODING TREE USES
• (i) Data can be encoded efficiently using Huffman Codes.
• (ii) It is a widely used and beneficial technique for compressing
data.
• (iii) Huffman's greedy algorithm uses a table of the frequencies
of occurrences of each character to build up an optimal way of
representing each character as a binary string.

4. WHAT IS HUFFMAN TREE…?
•Huffman coding is compression of message or bits.
•The most frequent character gets the smallest code and
the least frequent character gets the largest code.
(variable length coding)

5. TO FIND NUMBER OF BITS OF MESSAGE TYPES
•Fixed length coding.
•Variable length coding.

6. FIXED LENGTH CODING
• ASCII code.
• After applying compression.
Here 8 bits are required which are fixed so we call it as fixed length coding.

7. VARIABLE LENGTH CODING
• Here each character will be given a frequency (number of characters
repeated) .
• Step 1:- Draw Huffman tree.
• Step 2:- Assign the 0&1 value.
• Step 3:- Use formula to find number of bits.
• Formula:-
No. of frequency*No. of bits + No. of frequency*No. of bits+ ……

8. ON WHICH TECHNIQUE IT WORKS…
• Prefix code rule:-
No code is prefix of another code.
• Time complexity:-
--O(n log n)
-- Extracting minimum frequency from the priority queue takes place 2*(n-1) times
and its complexity is O(log n). Thus the overall complexity is O(nlog n).

9. POINTS TO REMEMBER
•All characters are present as a leaf node.
•Prefix rule is used to avoid ambiguity.
•In variable length coding there is no fixed length or code.

10. HUFFMAN’S ALGORITHM
1. Organize the data into a row as ascending order frequency
weights. Each character is leaf node of a tree.
2. Find two nodes with the smallest combined weights and join them
to form third node
3. This will form a new two level tree
4. The weight of new third node is addition of two nodes.
5. Repeat step 2 till all the nodes on every level are combined to
form a single tree

11. HUFFMAN CODING
• Huffman (C)
• 1. n=|C|
• 2. Q ← C
• 3. for i=1 to n-1
• 4. do
• 5. z= allocate-Node ()
• 6. x= left[z]=Extract-Min(Q)
• 7. y= right[z] =Extract-Min(Q)
• 8. f [z]=f[x]+f[y]
• 9. Insert (Q, z)
• 10. return Extract-Min (Q)

12. APPLICATIONS OF HUFFMAN’S CODING
•Huffman coding is used in conventional compression
formats like GZIP, BZIP2, PKZIP, etc.
•For text and fax transmissions.

21. Average code lenth = no of frequencies * no of bits
+ no of frequencies * no of bits+…….+n
Frequency= weight
Bits= length of code
ACL= 10*2 + 3*4+ 4*3+ 15*2+ 2*4 + 4*3 +
2*4 + 3*4
= 114

27. Practice Question
Suppose characters a, b, c, d, e, f
have probabilities 7, 9, 12, 22,
23, 27 respectively. Find an
optimal Huffman code and draw
the Huffman tree What is the
average code length