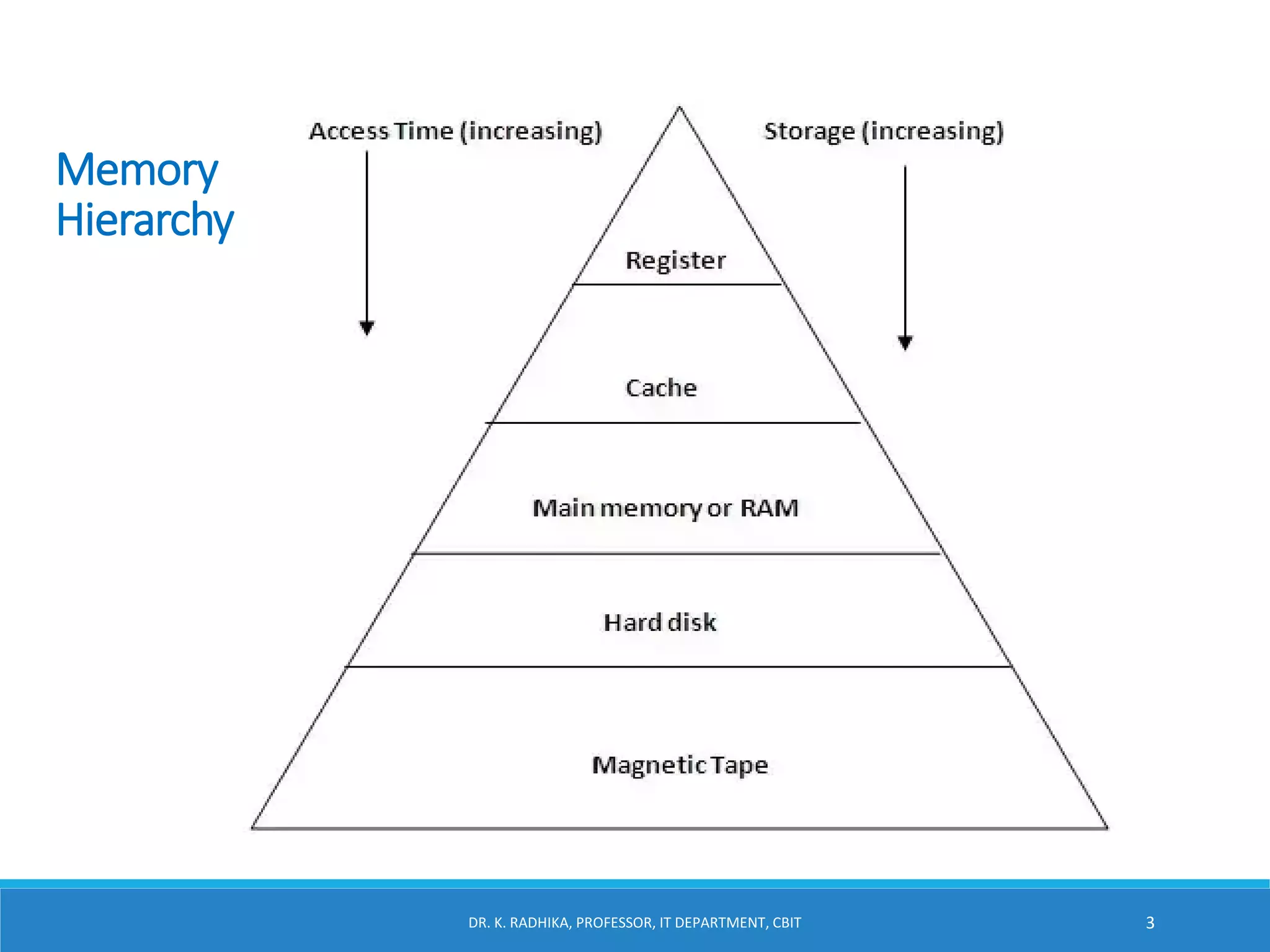
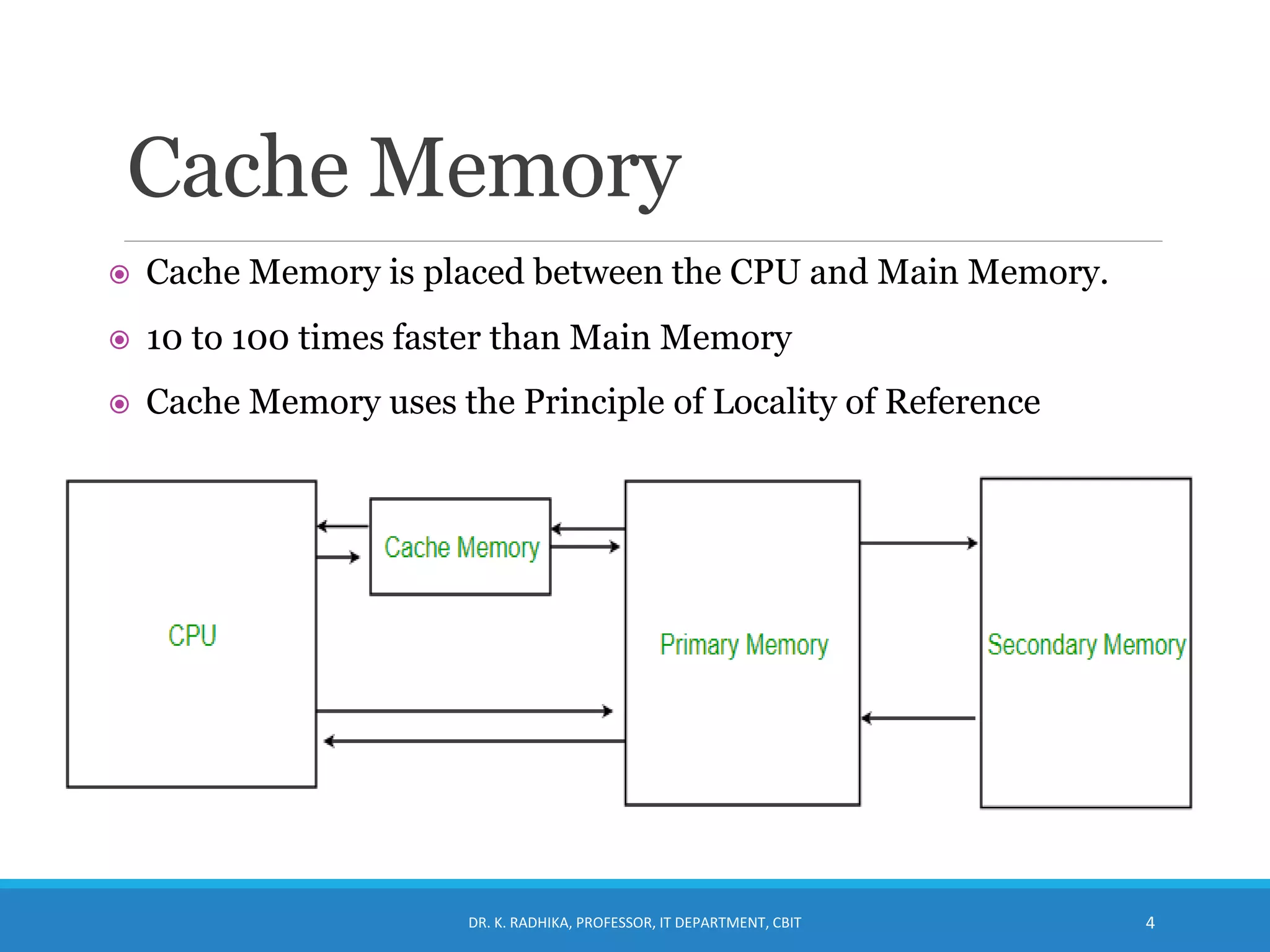
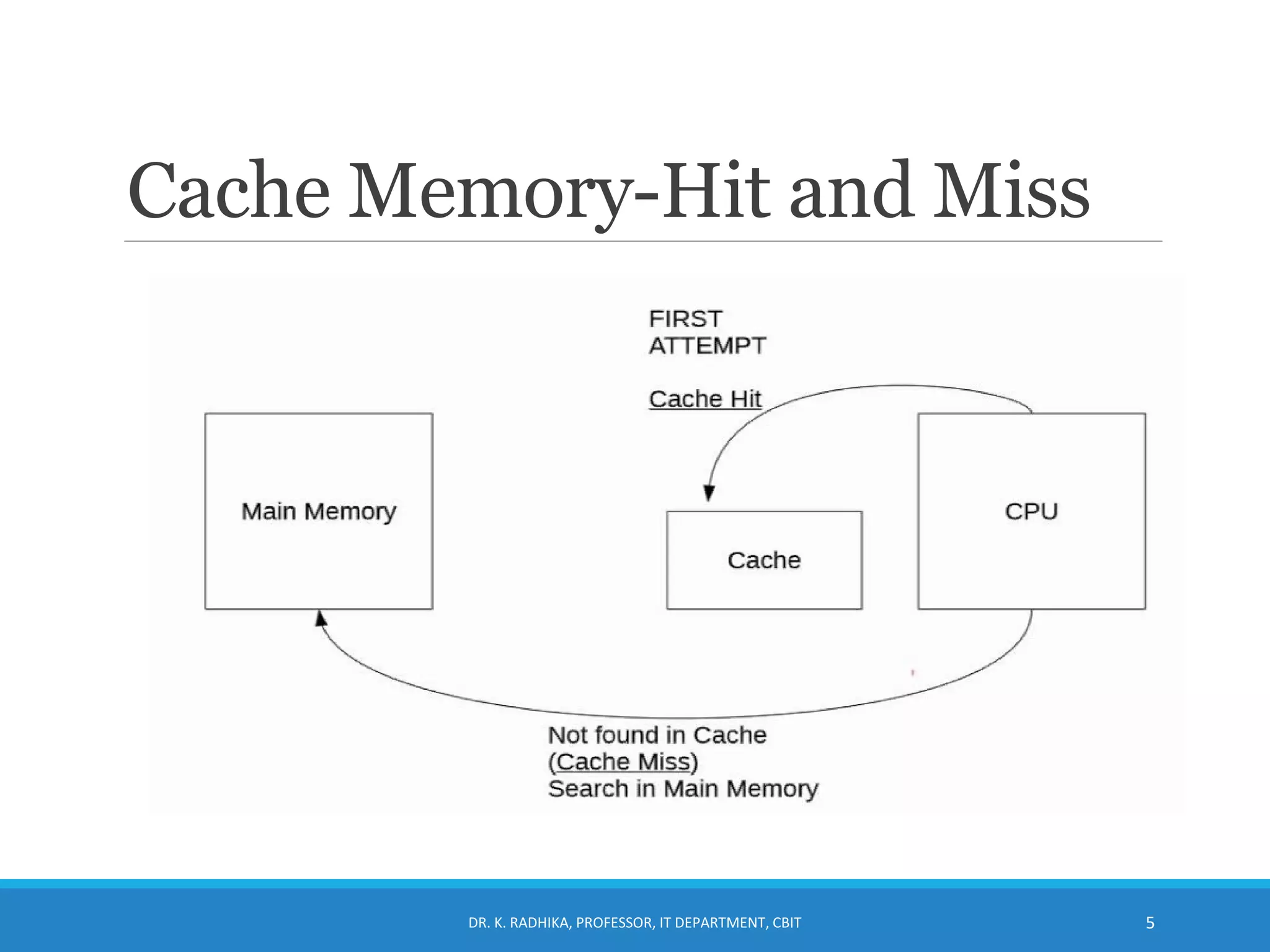
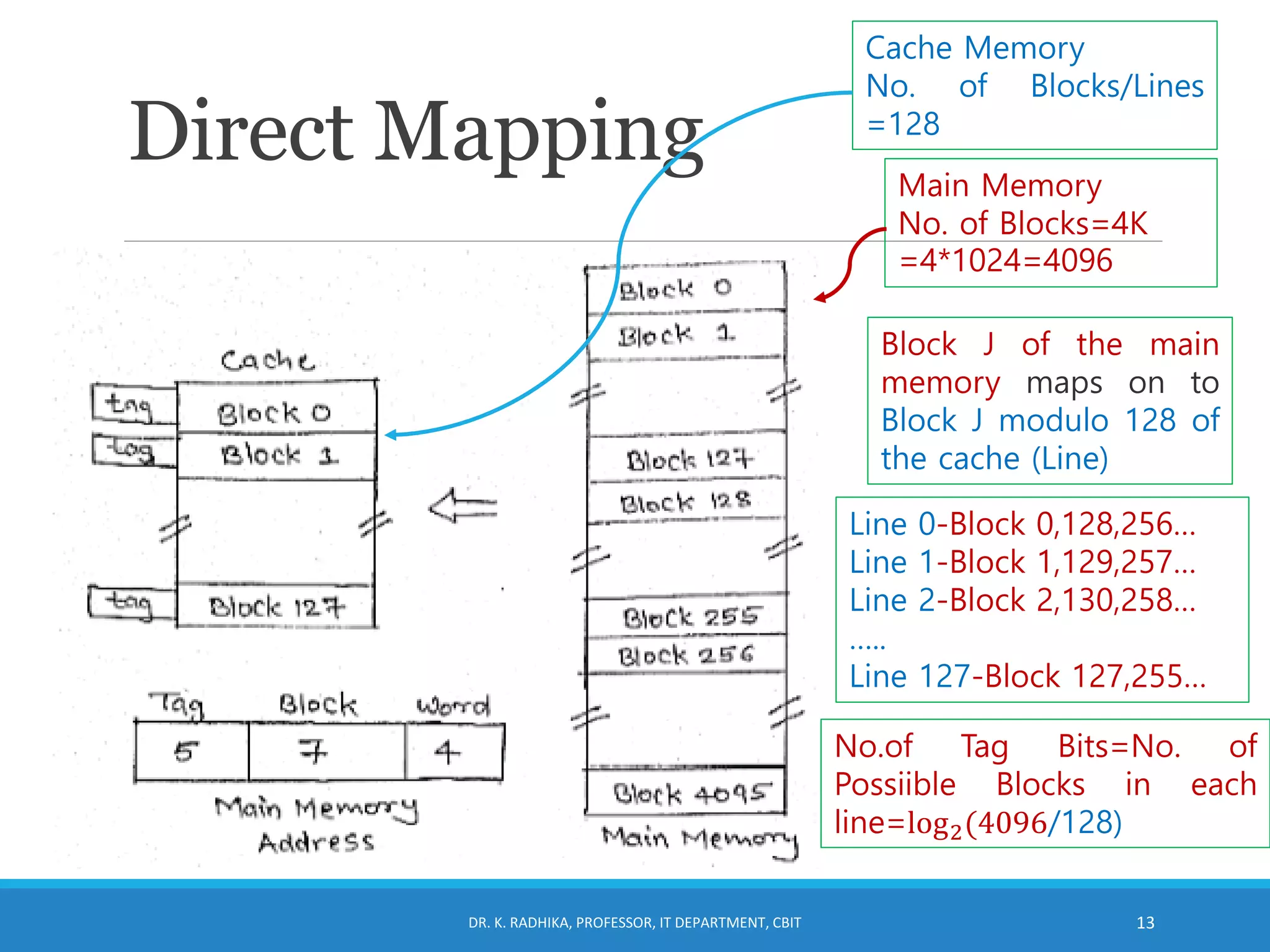
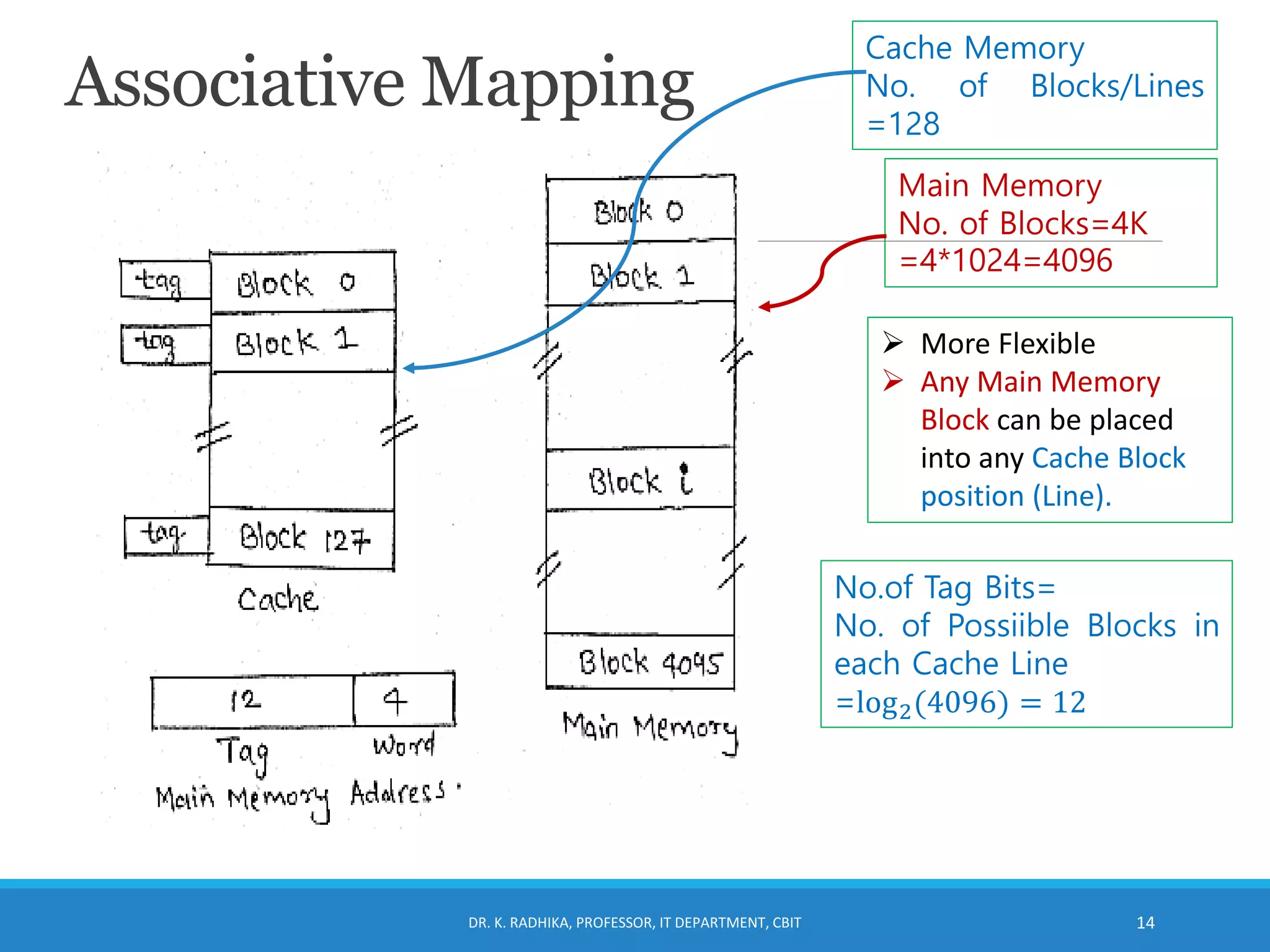
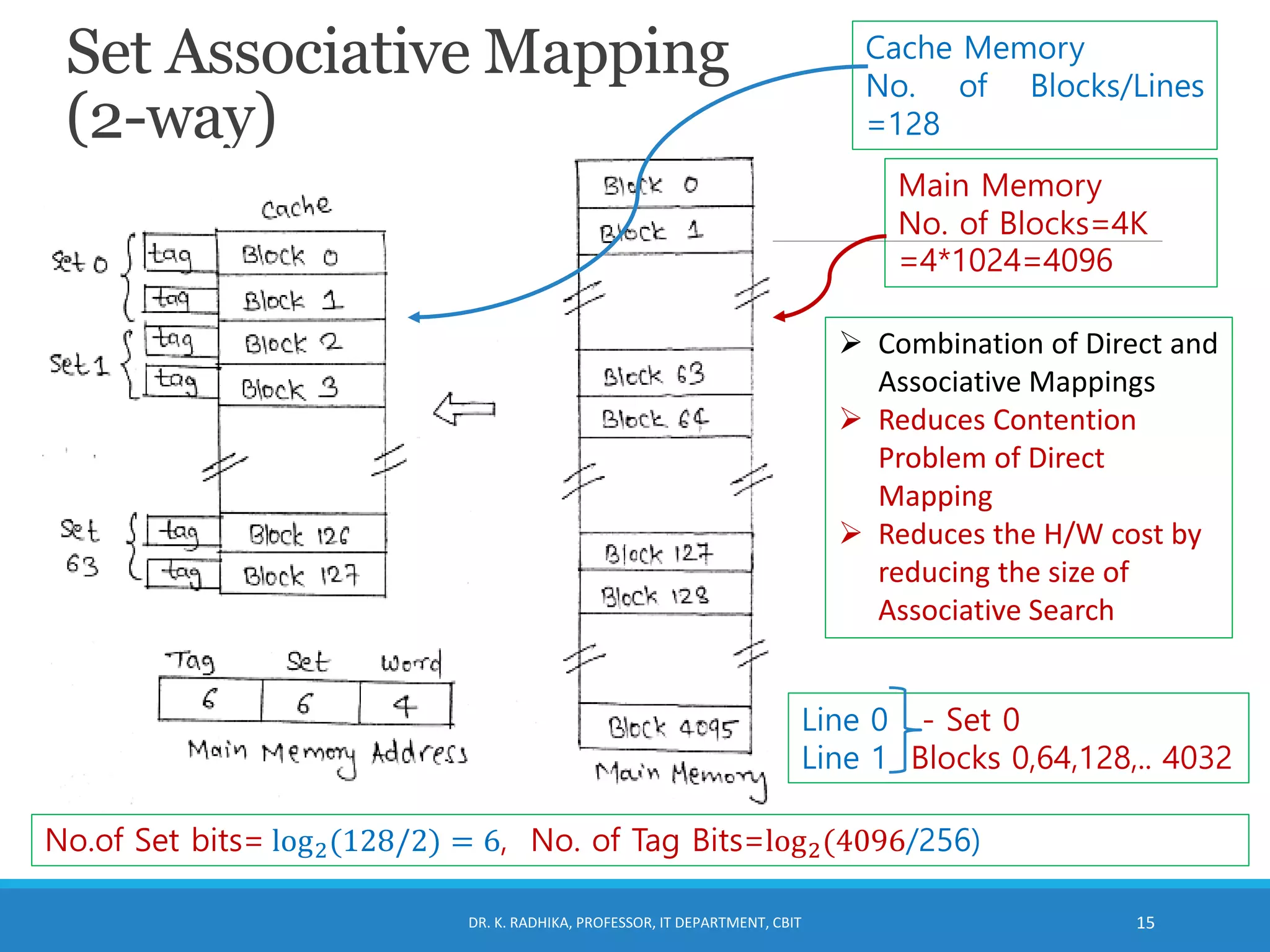
The document discusses cache memory organization. It describes how cache memory uses the principle of locality of reference to improve memory access time. It is placed between the CPU and main memory and is 10-100 times faster. The document introduces cache hit ratio and average memory access time formulas. It then covers different cache mapping techniques - direct mapping, associative mapping, and set-associative mapping which map blocks of main memory to blocks of cache memory. Examples of 2-way set associative mapping are provided.

1. Digital Logic and Computer
Architecture
UNIT-5
MEMORY ORGANIZATION
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 1

2. Topics to be Discussed
➢Cache Memory-Introduction
➢Cache Mapping Techniques
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 2

3. DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 3
Memory
Hierarchy

4. Cache Memory
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 4
 Cache Memory is placed between the CPU and Main Memory.
 10 to 100 times faster than Main Memory
 Cache Memory uses the Principle of Locality of Reference

5. Cache Memory-Hit and Miss
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 5

6. Principle of Locality of Reference
➢Cache Memory uses the Principle of Locality of Reference
➢Temporal locality of reference
The tendency of a computer Program to access the
same set of memory locations for a particular time period.
➢Spatial Locality of Reference
The tendency of the computer program to access
instructions whose addresses are near one another.
➢Average Execution Time α Average Memory Access Time
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 6

7. Hit Ratio & Average Memory Access Time
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 7
 Hit Ratio=
Total No. of Hits
Total No. of Memory Accesses by CPU
 Total No. of Memory Accesses= No. of Hits+ No. of
Misses
 Average Memory access time =
Tavg = h * Tc + (1-h)*(Tm + Tc)
 h- Probability of a Hit
 Tm-Main Memory Access Time
 Tc- Cache Memory Access Time

8. Problems
1. If a CPU has 39 Cache Hits and 2 Cache Misses
over a given timeframe, then find the Cache Hit
ratio. (Ans:
2. Calculate the average access time if cache
memory access time is 150ns and memory access
time is 900 ns and we have the hit ratio for cache
memory as h=0.8.
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 8

9. Problems
1. If a CPU has 39 Cache Hits and 2 Cache Misses
over a given timeframe, then find the Cache Hit
ratio.
(Ans: 0.95)
1. Calculate the average access time if cache
memory access time is 150ns and memory access
time is 900 ns and we have the hit ratio for cache
memory as h=0.8.
(Ans: 0.8*150+0.2*1050=330ns)
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 9

10. Cache Mapping Techniques
➢Entire Main Memory is divided into equal sized
Blocks.
➢Cache Memory is also divided into same-sized Blocks
➢Cache Mapping Technique defines mapping between
Blocks of Main Memory and Blocks of Cache Memory.
➢Direct Mapping
➢Associative Mapping
➢Set – Associative Mapping
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 10

11. DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 11
Cache Memory
Main Memory

12. Assumption
Consider a cache consisting of 128 blocks of 16
words each, for total of 2048 (2K) words and assume
that the main memory is addressable by 16 bit
address. Main memory is 64K which will be viewed
as 4K blocks of 16 words each.
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 12
Cache Memory
No. of Blocks=128
No. of Words=128 *16
=2048
=2*1024
=2K
Main Memory (16-bit Address)
No. of Words=216
= 26 * 210
= 64K
=16*4K
No. of Blocks=4K

13. Direct Mapping
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 13
Cache Memory
No. of Blocks/Lines
=128
Main Memory
No. of Blocks=4K
=4*1024=4096
Block J of the main
memory maps on to
Block J modulo 128 of
the cache (Line)
Line 0-Block 0,128,256…
Line 1-Block 1,129,257…
Line 2-Block 2,130,258…
…..
Line 127-Block 127,255…
No.of Tag Bits=No. of
Possiible Blocks in each
line=log2(4096/128)

14. Associative Mapping
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 14
Cache Memory
No. of Blocks/Lines
=128
Main Memory
No. of Blocks=4K
=4*1024=4096
➢ More Flexible
➢ Any Main Memory
Block can be placed
into any Cache Block
position (Line).
No.of Tag Bits=
No. of Possiible Blocks in
each Cache Line
=log2(4096) = 12

15. Set Associative Mapping
(2-way)
DR. K. RADHIKA, PROFESSOR, IT DEPARTMENT, CBIT 15
Cache Memory
No. of Blocks/Lines
=128
Main Memory
No. of Blocks=4K
=4*1024=4096
➢ Combination of Direct and
Associative Mappings
➢ Reduces Contention
Problem of Direct
Mapping
➢ Reduces the H/W cost by
reducing the size of
Associative Search
Line 0 - Set 0
Line 1 Blocks 0,64,128,.. 4032
No.of Set bits= log2(128/2) = 6, No. of Tag Bits=log2(4096/256)