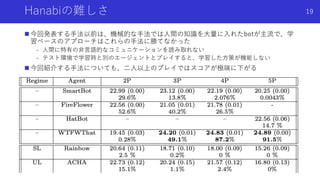
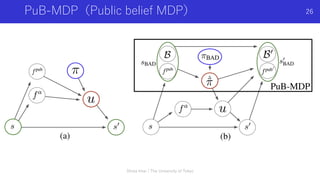
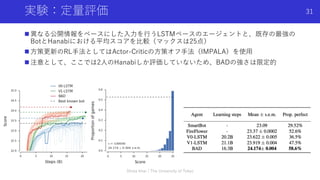
The document discusses applying theory of mind, or the ability to infer the intentions of other agents, to multi-agent reinforcement learning. It introduces three papers that use Bayesian reasoning to model other agents in the Hanabi game. Specifically, the papers develop methods for Bayesian action decoding and simplified action decoding to enable agents to reason about each other's intentions during both learning and testing. The document notes challenges in multi-agent reinforcement learning like non-stationarity from other agents learning and incomplete information about other agents. Applying theory of mind techniques may help address these challenges by allowing agents to infer what other agents know or intend to do.
![1
DEEP LEARNING JP
[DL Papers]
http://deeplearning.jp/
マルチエージェント強化学習と⼼の理論
〜Hanabiゲームにおけるベイズ推論を⽤いたマルチエージェント
強化学習⼿法〜
9/17 今井翔太 えるエル@ImAI_Eruel Matsuo Lab](https://image.slidesharecdn.com/0917imai1-210917021923/75/DL-Hanabi-1-2048.jpg)



![注意 / MARLに特有の概念
(CTDE; Centralized Learning Distributed Execution 中央集権型学習分散型実⾏)
n 現在のMARLの最重要概念(だが、今回の発表の本質ではない)
n 後ほど、「学習中はお互いの⽅策は既知」、「2種類の⾏動のうち⼀つを他のエージェ
ントに送信」など、普通の設定では⾮現実的な概念が出てくるが、MARLではこのCTDE
の仮定を置いて許容している
n 中央集権型学習:学習時のみ,勾配を計算する時に全体のエージェントの情報を含む環
境の「中央の状態」を使う
n 分散型実⾏:テスト時には,各エージェントは⾃⾝の部分観測のみを⼊⼒として⽅策を
実⾏
n COMA[Foerster+ 2017]以降,特に⽤いられるアプローチで,
“in many cases, learning can take place in a simulator or a laboratory in which extra
state information is available and agents can communicate freely”(Foerster+ 2016)
つまり,「マルチエージェントの学習は,研究的な環境でシミュレータ等を使えるため,
学習を促進するために追加の状態の情報を使ってもよい」という仮定によるアプローチ
n 当然,本来エージェントが動作するテスト環境は,基本的に各エージェントが個別の観
測だけを受け取って強調しているため,状態の追加情報は使えない
Shota Imai | The University of Tokyo
5](https://image.slidesharecdn.com/0917imai1-210917021923/85/DL-Hanabi-5-320.jpg)