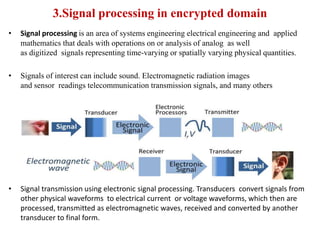
The document discusses the implementation of decimation in time-radix-2 FFT algorithms for signal processing in the encrypted domain. It covers the history and development of FFT algorithms, their computational efficiency, and how they can be applied to encrypted signals to maintain security and performance. Additionally, it highlights the benefits and challenges of performing operations on encrypted data using homomorphic encryption techniques.

1. Implementation of Decimation in Time-Radix-2
FFT Algorithms in Signal Processing of
Encrypted Domain(SPED)
AJAY KUMAR.M.ANNAIAH
Ph.D Research scholar
Dept of IT
NITK-Surathkal
ajaymodaliger@gmail.com

2. CONTENT

INTRODUCTION

REVIEW OF DFT –FFT ALGORITHM

TIME COMPLEXITY ANALYSIS OF RADIX-2

S.P.E.D

HOMOMORPHISM V/S SIGNAL ENCRYPTION

IMPLEMENTATION OF e-DFT

3. 1.Introduction
•
Discrete Fourier Transform(DFT) invented around 1805 by Carls Friedrich Gauss.
Limitation –computation time.
•
In the mid-1965 DFT is reinvented as The Fast Fourier Transform (FFT), By
Cooley-Tukey
•
FFT reduced the complexity of a Discrete Fourier Transform from O(N²), to
O(N·logN),
 purpose of reducing time complexity
 large number of Application developed
•
FFT algorithms became known as the Radix- 2 algorithm and was shortly
followed by the Radix-3, Radix-4, and Mixed Radix algorithms
•
Evaluation of research Fast Hartley Transform (FHT)and the Split Radix (SRFFT),
QFT. DITF

4. 2.Review of FFT Algorithms
•
The basic principle behind most Radix-based FFT algorithms is to exploit the
symmetry properties of a complex exponential that is the cornerstone of the
Discrete Fourier Transform (DFT). These algorithms
 Complex conjugate symmetry
 Periodicity
•
Divide the problem into similar sub-problems (butterfly computations) and achieve
a reduction in computational complexity.
•
All Radix algorithms are similar in structure differing only in the core computation
of the butterflies. The FHT differs from the other algorithms in that it uses a real
kernel
•
The DITF algorithm uses both the Decimation-In-Time (DIT) and Decimation-InFrequency (DIF) frameworks for separate parts of the
computation to achieve a reduction in the computational complexity.

5. Discrete Fourier Transform(DFT)

Allows us to compute an approximation of
the Fourier Transform on a discrete set of
frequencies from a discrete set of time
samples.
N 1
Xk
xn e
j2
k
n
N
for k
0, 1,, N 1
n 0



Where k are the index of the discrete
frequencies and n the index of the time samples
N  complex multiplies
N-1  complex addition

6. Symmetries properties of FFT

FFT algorithms exploits two symmetric properties
 Complex conjugate symmetry
K
W
N
N-n
WN
Kn *
N
Kn
W
 Periodicity
n
W
K
N
K N n
N
W
k N n
N
W
 Finally
WN
e
j2
k
n
N
Kn
or WN e
j2
k
n
N

7. Fast Fourier Transform

Cooley-Tukey algorithm:



Kn
WN e
j2
k
n
N
Based on decimation, leads to a factorization of
computations.
Let us first look at the classical radix 2
decimation in time.
FFT uses the Divide and conquer rule split the
Big DFT computation between odd and even
part
N 1
Xk
xn e
j2
k
n
N
for k
0, 1,, N 1
n 0
N 1
N 1
kn
x n WN
X k
n 0
kn
x n WN
n 0

8. Fast Fourier Transform



Consider and replace even and odd indices part
Even part of n2r
Odd part of n2r+1 for all r=0,1…N/2-1
N /2 1
N /2 1
k2r
x 2r WN
X k
r 0
N/2 1
Xk
k
x 2r 1 WN 2r
n 0
2 kr
N
N/2 1
2kr
x 2r 1 WN
x 2r W
r 0
2 kr
N
x 2r W
r 0
K
WN
n 0
N /2 1
X k
1
N /2 1
W
K
N
x 2r 1 W
n 0
2 Kr
N

9. Fast Fourier Transform
N /2 1
X k
2 kr
N
x 2r W
N /2 1
W
K
N
x 2r 1 W
r 0
n 0
Simplify the term

N/2 1
r 0
Xk

X k
e
WN
WN
2
N/2 1
kr
x 2r WN 2
Xk
2 Kr
N
K
WN
x 2r 1 WNkr2
n 0
K
WN X 0 k
Now the sum of two N/2 point DFT’s we
can use to get a N point DFT

10. 2 point Butterfly

Example if N=8 the even number[0,2,4,8]
odd number[0.3.5.7]
X(0)
X(1)
x(0)
x(2)
TFD N/2
•N/2(N/2-1) complex ‘+’ for each
N/2 DFT.
•(N/2)2 complex ‘ ’ for each
DFT.
x(N-2)
X(N/2-1)
W0
W1
x(1)
x(3)
We need:
-
X(N/2)
X(N/2+1)
•N/2 complex ‘ ’ at the input of
the butterflies.
•N complex ‘+’ for the butterflies.
•Grand total:
N2/2 complex ‘+’
TFD N/2
N/2(N/2+1) complex ‘ ’
WN/2-1
x(N-1)
N
2
2
-
X(N-1)
.2.......... .......... ......
N

11. Fast Fourier Transform

2.point FFT splitting in to multiple pass i.e.
N
N
2
2
2
.2.......... .......... ......
N
..... * N 4 ......... * N 8 ...... 8 * N 16
2
4
till

simplify the given form by applying
mathematical rule …

Finally computational time complexity of
Radix-2 FFT algorithm is
N log 2 N

12. Algorithm Parameters 2/2

The parameters are shown below:
1st stage
Node
Spacing
Butterflies
per group
Number of
groups
Twiddle
factor
2nd stage
3rd stage
…
Last stage
1
2
3
…
N/2
1
2
3
…
N/2
N/2
N/4
N/8
…
1
…

13. Algorithm Parameters

The FFT can be computed according to the
following pseudo-code:


For each stage
 For each group of butterfly
 For each butterfly
compute butterfly
 end
 end
end

14. Number of Operations

If N=2r, we have r=log2(N) stages. For each
one we have:



N/2 complex ‘ ’ (some of them are by ‘1’).
N complex ‘+’.
Thus the grand total of operations is:


N/2 log2(N) complex ‘ ’.
N log2(N) complex ‘+’.
N
128
1024
4096
+
896
10240
49152
x
448
5120
24576
These counts can be compared with the ones for the DFT

15. 3.Signal processing in encrypted domain
•
Signal processing is an area of systems engineering electrical engineering and applied
mathematics that deals with operations on or analysis of analog as well
as digitized signals representing time-varying or spatially varying physical quantities.
•
Signals of interest can include sound. Electromagnetic radiation images
and sensor readings telecommunication transmission signals, and many others
•
Signal transmission using electronic signal processing. Transducers convert signals from
other physical waveforms to electrical current or voltage waveforms, which then are
processed, transmitted as electromagnetic waves, received and converted by another
transducer to final form.

16. 4. Encrypted Signal processing
• Statistical signal processing – analyzing and extracting information from signals
and noise based on their stochastic properties
• Spectral estimation – for determining the spectral content (i.e., the distribution
of power over frequency) of a time series
• Audio signal processing – for electrical signals representing sound, such as
speech or music
• Speech signal processing – for processing and interpreting spoken words
• Image processing – in digital cameras, computers and various imaging systems
• Video processing – for interpreting moving pictures
• Filtering – used in many fields to process signals
• Time-frequency analysis – for processing non-stationary signals

17. 5.Signal processing module v/s cryptosystem
• Signal processing modules working directly on encrypted Signal data
provide better solution to application scenarios
• valuable signals must be protected from a malicious processing device.
• investigate the implementation of the discrete Fourier transform (DFT)
in the encrypted domain, by using the homomorphic properties of the
underlying cryptosystem.
• Several important issues are considered for the direct DFT, the radix2, and the radix-4 fast Fourier algorithms, including the error analysis
and the maximum size of the sequence that can be transformed.
• The results show that the radix-4 FFT is best suited for an encrypted
domain implementation. With computational complexity and error
analysis

18. 6.Traditional approach of signal Encryption
• Most of technological solutions proposed issues of multimedia security rely
on the use of cryptography.
• Early works in this direction by applying cryptographic primitives, is to
build a secure layer on top of signal application.
• secure layer is able to protect them from leakage of critical information
Signal processing modules.
•
Examples of such an approach include the encryption of content before its
transmission or storage (like encrypted digital TV channels), or wrapping
multimedia objects into an encrypted system with an application (the
reader)
• encryption layer is used only to protect the data against third parties and
authorized to access the data.
• signal processing tools capable of operating directly on encrypted data
highlighting the benefits offered by the availability

19. 7.Public key cryptography for signal encryption

20. Homomorphism for encrypted domain
•
•
Homomorphic encryption is a concept where specific computations can be
performed on the cipher text of a message. The result of these computations is the
same as if the operations were performed on the plaintext first and encrypted
afterwards. So homomorphic encryption allows parties who do not have an
decryption key and thus don't know the plaintext value, still perform computation
on this value
The two group homomorphism operations are the arithmetic addition and
multiplication.
•
A homomorphic encryption is additive is
E(x + y) = E(x) . E(y)
1) where E denotes an encryption function, 2) . denotes an operation depending on
cipher
3) x and y are plaintext messages.
•
A homomorphic encryption is multiplicative if:
E(x y) = E(x)
. E(y)

21. Homomorphism signal encryption Signal encryption
Homomorphism encryption

22. simple example of how a homomorphic encryption
scheme might work in cloud computing:
• Company X has a very important data set (VIDS) that consists of the
numbers 5 and 10. To encrypt the data set, Company X multiplies each
element in the set by 2, creating a new set whose members are 10 and 20.
• Company X sends the encrypted VIDS set to the cloud for safe storage. A
few months later, the government contacts Company X and requests the
sum of VIDS elements.
• Company X is very busy, so it asks the cloud provider to perform the
operation. The cloud provider, who only has access to the encrypted data
set, finds the sum of 10 + 20 and returns the answer 30.
• Company X decrypts the cloud provider’s reply and provides the
government with the decrypted answer, 15.

23. Encrypted domain DFT (e-DFT)

Consider the DFT sequence x(n) is defined as :
N 1
X k
xn e
j2
k
n
N
for k
0, 1,  , N 1
n 0
N 1
X k
xnW
nk
for k
0, 1,, N 1
n 0


w and x(n) is a finite duration sequences with
length M
Consider the scenario the where electronic
processor fed the input data signal as encrypted
data format as in digital form such as 0’s and 1’s

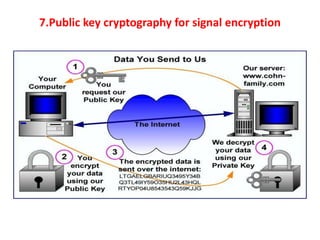
24. Encrypted domain DFT (e-DFT)

Encrypted input data signal in the form
of digital 0’s and 1’s in the form of
equation

E(X)=(E[x(0)],E[x(1)],…..E[x(N-1)]
in order to make possible linear
computation for encrypted input signal
use homographic technique of Additive
that is represented by
E(x + y) = E(x)
. E(y)

25. Encrypted domain DFT (e-DFT)
• Issues of DFT in SPED is
• both input sample of encrypted signal and DFT
coefficients need to represented as integer values
• Paillier homographic cryptosystem uses modular
operation
• Uses of FFT-Radix 4 reduces the time complexity in
SPED and best suited for encryption

26. .
THANK YOU