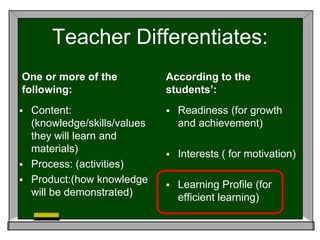
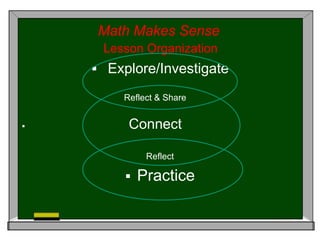
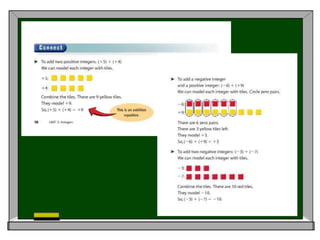
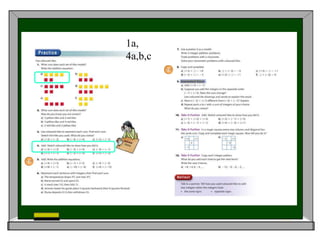
This document discusses differentiated instruction strategies for teaching math. It defines differentiated instruction as proactively planning to meet diverse student needs by focusing on learning outcomes and adjusting the content, process, or product based on student readiness, interests, and learning profiles. Examples of strategies discussed include using learning stations, the anticipation guide pre-assessment technique, and determining student learning styles. The "new math" approach emphasizes exploring problems, reflecting on different strategies, and having students explain their reasoning over traditionally teaching a single procedure.

1. Differentiated Instruction
for Teaching the “New” Math
“One Size Does NOT Fit All”
Beverly Ptolemy
and
Jade Ballek

2. Anticipation Guide
 An anticipation guide is a form
of pre-assessment.
 If helps teachers determine
student readiness.
 True or False Activity

3. Determining Your
Learning Style
The VAK Inventory

4. What is Differentiated Instruction?
What differentiated
instruction is:
 a mind set where the
teacher proactively
plans to meet the
diverse needs of
students
 The learning outcome is
the focus for all
What differentiated
instruction is not:
 Not individual lesson
plans for each student
 Not “dumbing down”
curriculum
 Not assigning busy work
for enrichment

5. Teacher Differentiates:
One or more of the
following:
 Content:
(knowledge/skills/values
they will learn and
materials)
 Process: (activities)
 Product:(how knowledge
will be demonstrated)
According to the
students’:
 Readiness (for growth
and achievement)
 Interests ( for motivation)
 Learning Profile (for
efficient learning)

6. Learning Styles in Math
Classrooms
Visual
Ask students to translate a problem into a picture.
Auditory
Ask students to explain concepts to each other to see if there
are different ways of understanding
Kinesthetic
Use a number line on the floor to have students move as
positive and negative numbers

7. Partner Pair Share
 Think about your own learning
experiences. Discuss with a partner.
 Did you ever realize that there are different learning
styles?
 Were you given a chance to find out about your own
learning style?
 Did your teacher offer a variety activities to meet
different learning styles?
 Do you think this would have been helpful?

8. What you might see in a
differentiated math class
 Students may not all be working on the same task
 Some students may be working individually; some may be in
groups
 The teacher may be guiding groups, teaching whole group
sessions or working individually with students
 Students will be encouraged to use more than one method of
finding the answer to a problem
 Activities and assessments are based on the curriculum
outcomes
 Flexible groups are planned
 On-going assessment

9. What is “new”
about our
approach to
math?

10. Typical Classroom Procedures
Traditional Approach:
1. Teacher models a procedure
2. Students practise by doing
assignment, usually
individually, following
procedure taught
3. Teacher assesses
periodically
New Approach:
1. students explore a problem
individually or in groups
2. students reflect & share the
strategies they used with the
class
3. teacher connects what the class
did, and models more examples,
gives handouts, etc.
4. students practice by doing the
assignment using multiple
strategies, explaining/showing as
they go
5. teacher assesses and this drives
next lesson

11. Math Makes Sense
Lesson Organization
 Explore/Investigate
Reflect & Share
 Connect
Reflect
 Practice

12. Why the Change?
 Low scores on international testing, compared
to other countries who use a problem- based,
constructivist approach
 Brain research & constructivist theory shows
deep understanding occurs when students
actively problem solve & construct their own
meaning

13. Learning Process
1. Begin by using manipulatives to create an
understanding of why
2. Then use pictures to represent the understanding
3. Next, use symbols and do the procedure that comes
from understanding manipulatives and pictures
4. Finally, reflect and explain the how’s & why’s

14. How has math changed?
 Lessons take more time (often multi-day)
 More hands on math through the use of manipulatives
 Students reflect/explain/show what they did
 Many strategies introduced, not just one “correct” procedure
taught
 Problem solving occurs in all parts of the lesson

15. A Model Lesson
Adding Integers Using Tiles
Math Makes Sense 7

18. Adding Integers Using Tiles
Connect: p 56-57
(using technology)
Online Integers

19. 1a,
4a,b,c

20. Instructional Strategies that
Support Differentiation
Learning Stations

21. Stations
 Stations are different locations in the classroom
where students work on different tasks in
groups.
 It allows students to work with different group
members on different tasks.
 It allows teachers to address different learning
styles through different activities.

22. Station Instructions
 1. Find a partner.
 2. Each group needs to go to a station.
 3. You will have 10 minutes at each station to
complete the activity. The buzzer will indicate
when it is time to move to the next station.
 4. If you complete your activity before the time
is up, begin working on your reflection.
 5. Work cooperatively!!!

23. Stations
 Grade 1 -- Patterns
 Grade 2 – Measurement
 Grade 4 – Addition Using Base Ten Blocks
 Grade 5 -- Multiplication Using Arrays (Smart
Board)
 Grade 7 -- Area of a Triangle Using Geoboards

24. Wrapping Things Up
 Reflect and share
– Complete your reflection sheet
 Questions

25. Exit Slip
32075
CAST #www.polleverywhere.com