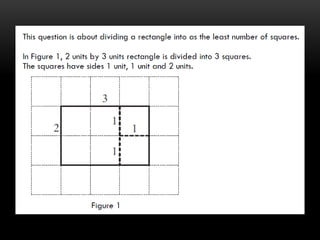
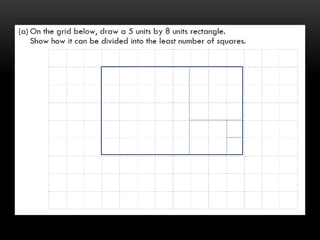
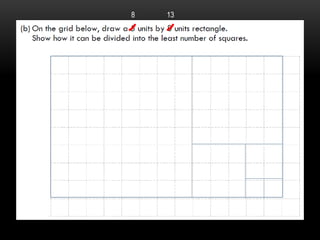
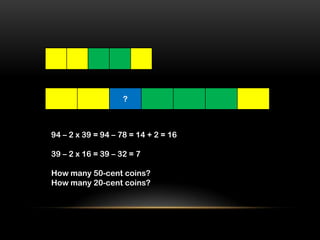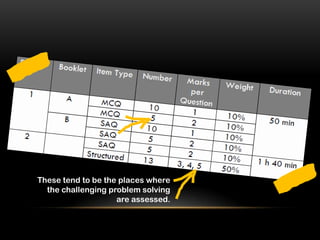
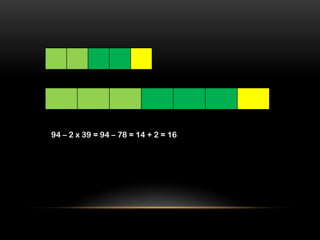
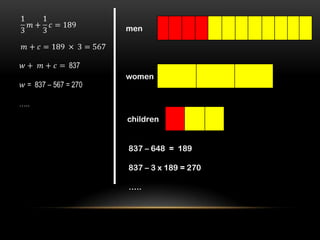
This document provides information about coaching children in primary mathematics for the PSLE: 1) It discusses 3 things about problem solving in the PSLE and 2 sections that assess challenging problem solving. 2) It outlines a 5-step process to help children with challenging problems and provides 2 examples demonstrating the steps. 3) Marshall Cavendish Institute is offering a 4-session workshop for parents/tutors to understand the primary math curriculum and coach topics like fractions, geometry, word problems, and algebra.

1. PSLE Mathematics
Yeap Ban Har
Marshall Cavendish Institute
yeapbanhar@gmail.com

2. www.moe.edu.sg/education/syllabuses

3. 3 Things About
Problem Solving
in PSLE

4. 

5. 

6. 

7. 2 Sections in
PSLE with
Challenging
Problems

8. These tend to be the places where
the challenging problem solving
are assessed.

9. 5 Steps to help
Your Child with
Challenging
Problems

11. 2 Examples to
Show the Five
Steps

12. The speaker is demonstrating what an adult helping
children does. What does an adult do to help
children manage their reading?

13. Solution:
2 fifths of 20-cent coins + 3 sevenths of 50-cent coins  39 coins
4 fifths of 20-cent coins + 6 sevenths of 50-cent coins  2 x 39 coins = 78 coins
1 fifth of 20-cent coins + 1 sevenths of 50-cent coins  94 – 78 = 16
5 fifths of 20-cent coins + 5 sevenths of 50-cent coins  5 x 16 = 80
2 sevenths of 50-cent coins  94 – 80 = 14
There are 14 2 x 7 = 49 fifty-cent coins.
There are 94 – 49 = 45 twenty-cent coins.
Sally had 49 x 50 cents + 45 x 20 cents or $33.50.
Answer:$33.50

17. 94 – 2 x 39 = 94 – 78 = 14 + 2 = 16

18. 94 – 2 x 39 = 94 – 78 = 14 + 2 = 16

19. 94 – 2 x 39 = 94 – 78 = 14 + 2 = 16

20. ?
94 – 2 x 39 = 94 – 78 = 14 + 2 = 16

21. ?
94 – 2 x 39 = 94 – 78 = 14 + 2 = 16
39 – 2 x 16 = 39 – 32 = 7
How many 50-cent coins?
How many 20-cent coins?

29. Solution:
(a) (3m + 6) cm
(b) length = 3 x 4 cm + 6 cm = 18 cm and width = 3 cm
area = 18 cm x 3 cm = 54 cm2

30. 2 Common and
1 Unusual
Challenging
Problems

32. 9 parts 6 parts 5 parts $120  16 parts
$30  4 parts
$150  20 parts
He had $150 at first.

33. compare

34. men
women
837 – 648 = 837 – 637 – 11 = 200 – 11 = 189
1 third of the men + 1 third of the children  189
men + children  189 x 3 = 570 – 3 = 567
women  837 – 567 = 837 – 537 – 30 = 270
men  270 3 x 4 = 90 x 4 = 360
children  837 – 360 – 270 = 837 – 630 = 207
There were 207 children at first.

35. men
women
children
837 – 648 = 189
837 – 3 x 189 = 270
…..

39. 8 13

40. 2 3 4 5 6
13 x ? 13 x 21 What is the
dimensions of the
21 x ? 21 x 34 rectangle with the
least number of
squares being 10?

41. See
patterns, trends

42. MARSHALL CAVENDISH INSTITUTE’S
WORKSHOP FOR PARENTS:
COACHING CHILDREN IN PRIMARY
MATHEMATICS PROGRAMME
(BATCH 2)
(END OF JUNE – SEPT 2012)
 4-Session Programme for Parents / Tutors
 Understand the Mathematics curriculum for different
primary levels
 Topics like Fractions, Geometry, Word Problem Solving and
Algebra will be covered
 Please contact geraldynsng@sg.marshallcavendish.com
 Class size of about 30.