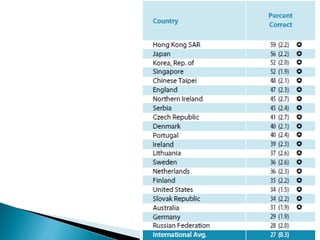
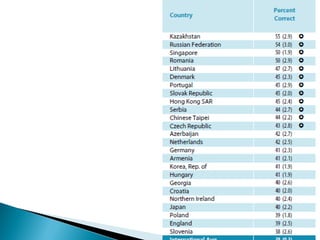
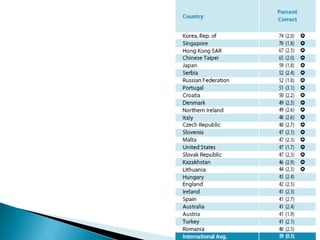
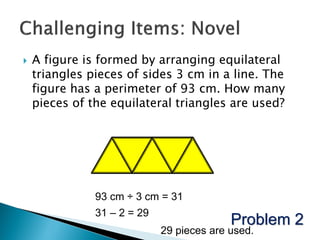
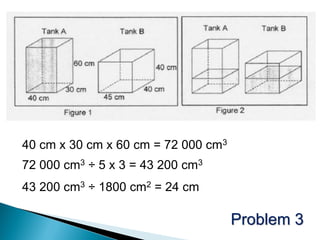
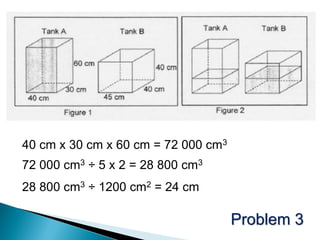
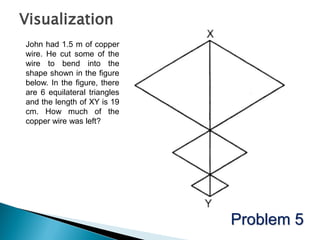
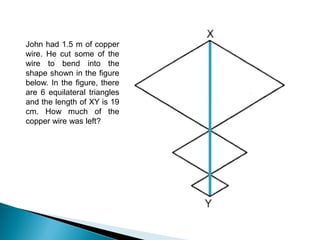
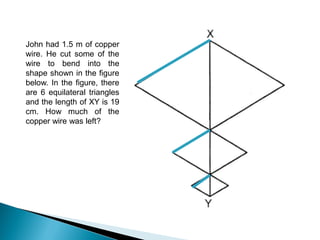
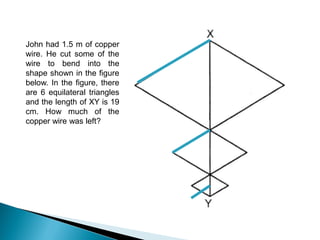
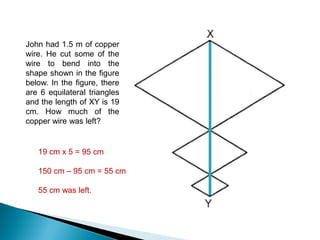
Here are some tips for improving problem solving skills in PSLE Mathematics: - Take time to understand the question fully before attempting to solve it. Re-read if needed. - Look for key information like numbers, operations, shapes etc and think about how they might be related. - Draw diagrams or make lists when working with multiple steps, relationships or parts. This helps organize your thinking. - Estimate answers before calculating to check if your working makes sense. - Check your work - go back and ensure steps are correct and you have not made computational errors. - Practice explaining your reasoning and showing your working, as this helps develop logical thinking skills. - Review incorrect or challenging questions again later

1. Problem Solving in
PSLE Mathematics
Yeap Ban Har
Marshall Cavendish Institute
Singapore
banhar.yeap@pathlight.org.sg
Slides are available at
www.banhar.blogspot.com

4. Type Mark Number Type Mark Number
Value Value
MCQ 1 mark 10 (10%) SAQ 2 marks 5 (10%)
MCQ 2 marks 5 (10%) 3 marks
SAQ 1 mark 10 (10%) LAQ 4 marks 13 (50%)
5 marks
SAQ 2 marks 5 (10%)
Paper 1 (50 min) Paper 2 (1 hr 40 min)

5. Type Mark Number Type Mark Number
Value Value
MCQ 1 mark 10 (10%) SAQ 2 marks 10 (20%)
MCQ 2 marks 10 (20%) 3 marks
SAQ 2 marks 10 (20%) LAQ 4 marks 8 (30%)
5 marks
Paper 1 (1 hr) Paper 2 (1 hr 15 min)

10. The rationale of teaching mathematics is that it is “a good
vehicle for the development and improvement of a
person’s intellectual competence”.

11. Ministry of Education 2006

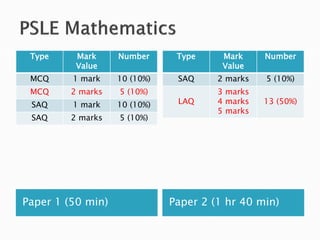
12. Find the value of 12.2 ÷ 4 .
Answer : 3.05 [B1]
Example 1

13. 3 .05
12.20 4 12.20
12
12 20 hundredths
0.20
Number Bond Method 0.20
0
Long Division Method

14. A show started at 10.55 a.m. and ended
at 1.30 p.m. How long was the show in
hours and minutes?
2 h 30 min
11 a.m. 1.30 p.m.
Answer : 2 h 35 min [B1]
Example 2

15.  Find <y in the figure below.
70 o
70 o y
70 o
 360o – 210o = 150o
Example 3

16. The height of the classroom door is about __.
(1) 1m
(2) 2m
(3) 10 m
(4) 20 m
Example 4

17. Ministry of Education 2006

18. Cup cakes are sold at 40 cents each.
What is the greatest number of cup cakes that
can be bought with $95?
 $95 ÷ 40 cents = 237.5
Answer: 237 cupcakes
Example 5

19. From January to August last year, Mr
Tang sold an average of 4.5 cars per
month, He did not sell any car in the
next 4 months. On average, how many
cars did he sell per month last year?
4.5 x 8 = 
36 ÷ 12 = 3
Answer: 3 cars / month
Example 6

20. Mr Tan rented a car for 3 days. He was
charged $155 per day and 60 cents for
every km that he travelled. He paid
$767.40. What was the total distance
that he travelled for the 3 days?
$767.40 – 3 x $155 = $302.40
$302.40 ÷ 60 cents per km = 504 km
Example 7

21. Mr Tan rented a car for 3 days. He was
charged $155 per day and 60 cents for
every km that he travelled. He paid
$767.40. What was the total distance
that he travelled for the 3 days?
767.40 – 3 x 155 = 302.40
302.40 ÷ 0.60 = 504
He travelled 504 km.
Example 7

22. Ministry of Education 2006

23. Ministry of Education 2006

24. Parents Up In Arms Said Mrs Vivian Weng: "I think the setters
feel it'll be faster for them to compute with a
Over PSLE calculator. So the problems they set are much
more complex; there are more values, more
steps. But it's unfair because this is the first
Mathematics Paper time they can do so and they do not know
what to expect!"
TODAY’S 10 OCT 2009 …
"The introduction of the use of calculators
does not have any bearing on the difficulty of
SINGAPORE: The first thing her son did when he came out from paper. The use of calculators has been
the Primary School Leaving Examination (PSLE) maths paper on introduced into the primary maths curriculum
Thursday this week was to gesture as if he was "slitting his so as to enhance the teaching and learning of
throat". maths by expanding the repertoire of learning
"One look at his face and I thought 'oh no'. I could see that he felt activities, to achieve a better balance between
he was condemned," said Mrs Karen Sng. "When he was telling the time and effort spent developing problem
me about how he couldn't answer some of the questions, he got solving skills and computation skills.
very emotional and started crying. He said his hopes of getting Calculators can also help to reduce
(an) A* are dashed." computational errors."
…
Not for the first time, parents are up in arms over the PSLE Another common gripe: There was not
Mathematics paper, which some have described as "unbelievably enough time for them to complete the paper.
tough" this year. As recently as two years ago, the PSLE A private tutor, who declined to be named,
Mathematics paper had also caused a similar uproar. told MediaCorp she concurred with parents'
The reason for Thursday's tough paper, opined the seven parents opinions. "This year's paper demanded more
whom MediaCorp spoke to, was because Primary 6 students were from students. It required them to read and
allowed to use calculators while solving Paper 2 for the first time. understand more complex questions, and go
… through more steps, so time constraints would
have been a concern," the 28-year-old said.

25. Students in the highest international benchmark are able
to apply their knowledge in a variety of situations and
able to explain themselves.

34. Ministry of Education 2006

35. 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
Problem 4

36. Table 1 consists of numbers from 1 to 56. Kay and Lin are given a plastic
frame that covers exactly 9 squares of Table 1 with the centre square
darkened.
(a) Kay puts the frame on 9 squares as shown in the figure below.
3 4 5
11 13
19 20 21
What is the average of the 8 numbers that can
be seen in the frame?

37. Table 1 consists of numbers from 1 to 56. Kay and Lin are given a plastic
frame that covers exactly 9 squares of Table 1 with the centre square
darkened.
(a) Kay puts the frame on 9 squares as shown in the figure below.
3+4+5+11+13+19+20 = 96
3 4 5 96 ÷ 8 = 12
11 13 Alternate Method
4 x 24 = 96
19 20 21 96 ÷ 8 = 12
What is the average of the 8 numbers that can
be seen in the frame?

38. (b) Lin puts the frame on some other 9 squares.
The sum of the 8 numbers that can be seen in the frame is 272.
What is the largest number that can be seen in the frame?
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56

39.  A figure is formed by arranging equilateral
triangles pieces of sides 3 cm in a line. The
figure has a perimeter of 93 cm. How many
pieces of the equilateral triangles are used?
93 cm ÷ 3 cm = 31
31 – 2 = 29
Problem 2
29 pieces are used.

40. 40 cm x 30 cm x 60 cm = 72 000 cm3
72 000 cm3 ÷ 5 x 3 = 43 200 cm3
43 200 cm3 ÷ 1800 cm2 = 24 cm
Problem 3

41. 40 cm x 30 cm x 60 cm = 72 000 cm3
72 000 cm3 ÷ 5 x 2 = 28 800 cm3
28 800 cm3 ÷ 1200 cm2 = 24 cm
Problem 3

42. Rena used stickers of four different shapes
to make a pattern. The first 12 stickers are
shown below. What was the shape of the
47th sticker?
            ………?
1st 12th 47th
Problem 4

43. Weiyang started a savings plan by putting 2
coins in a money box every day. Each coin was
either a 20-cent or 50-cent coin. His mother
also puts in a $1 coin in the box every 7 days.
The total value of the coins after 182 days was
$133.90.
(a) How many coins were there altogether?
(b) How many of the coins were 50-cent coins?
Problem 5

44. Weiyang started a savings plan by putting 2
coins in a money box every day. Each coin was
either a 20-cent or 50-cent coin. His mother
also puts in a $1 coin in the box every 7 days.
The total value of the coins after 182 days was
$133.90.
(a) How many coins were there altogether?
(b) How many of the coins were 50-cent coins?
182  7 = 20 + 6 = 26
182 x 2 + 26 = 364 + 26 = 390
There were 390 coins altogether.
Problem 5

45. Weiyang started a savings plan by putting 2
coins in a money box every day. Each coin was
either a 20-cent or 50-cent coin. His mother
also puts in a $1 coin in the box every 7 days.
The total value of the coins after 182 days was
$133.90.
(a) How many coins were there altogether?
(b) How many of the coins were 50-cent coins?
$133.90 - $26 = $107.90
50-cent 20-cent
 
There were  50-cent coins.

46. Suppose each day he put in one 20-cent and
one 50-cent coins, the total is $127.40
But he only put in $107.90 ..
to reduce this by $19.50, exchange 50-cent
for 20-cent coins
$19.50  $0.30 = 65
There were 182 – 65 = 117 fifty-cent coins.

47. Visualization
John had 1.5 m of copper
wire. He cut some of the
wire to bend into the
shape shown in the figure
below. In the figure, there
are 6 equilateral triangles
and the length of XY is 19
cm. How much of the
copper wire was left?
Problem 5

48. John had 1.5 m of copper
wire. He cut some of the
wire to bend into the
shape shown in the figure
below. In the figure, there
are 6 equilateral triangles
and the length of XY is 19
cm. How much of the
copper wire was left?

49. John had 1.5 m of copper
wire. He cut some of the
wire to bend into the
shape shown in the figure
below. In the figure, there
are 6 equilateral triangles
and the length of XY is 19
cm. How much of the
copper wire was left?

50. John had 1.5 m of copper
wire. He cut some of the
wire to bend into the
shape shown in the figure
below. In the figure, there
are 6 equilateral triangles
and the length of XY is 19
cm. How much of the
copper wire was left?

51. John had 1.5 m of copper
wire. He cut some of the
wire to bend into the
shape shown in the figure
below. In the figure, there
are 6 equilateral triangles
and the length of XY is 19
cm. How much of the
copper wire was left?
19 cm x 5 = 95 cm
150 cm – 95 cm = 55 cm
55 cm was left.

52. Problem 7

53. 1 2

4 9
Problem 7

54.  Number Sense
 Patterns
 Visualization
 Communication
 Metacognition

55.  Try to do as you read the problems. Do not
wait till the end of the question to try to do
something.
 Try to draw when you do not get what the
question is getting at. Diagrams such as
models are very useful.
 Do more mental computation when practising
Paper 1.