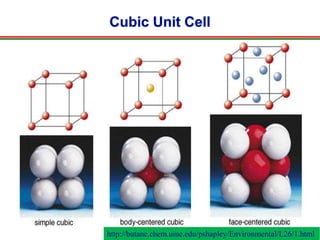
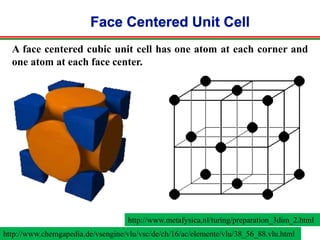
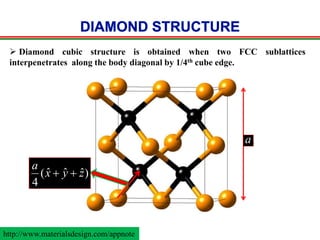
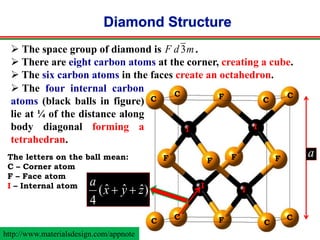
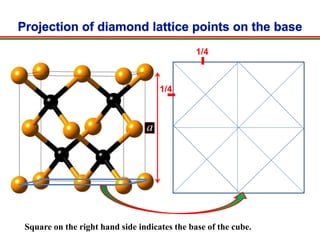
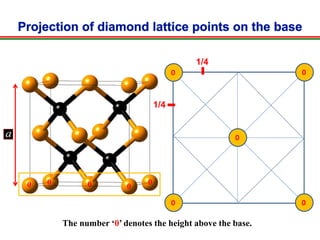
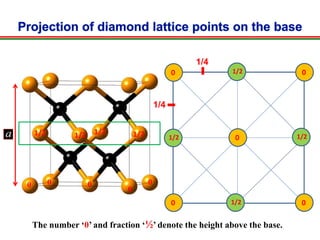
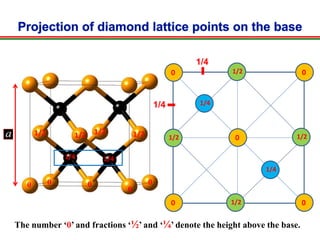
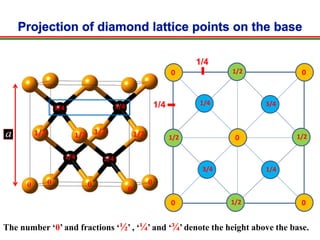
The document discusses the structure of diamond and face-centered cubic (fcc) unit cells, detailing atom positioning, space group, and atomic packing factor calculations. It highlights that the diamond cubic structure is formed by two interpenetrating fcc sublattices and provides formulas to compute the atomic packing factor. Additional resources and contact information are provided for further inquiries.

1. Dr. Virendra Kumar Verma
Madanapalle Institute of Technology and Science (MITS)

2. http://butane.chem.uiuc.edu/pshapley/Environmental/L26/1.html

3. http://www.metafysica.nl/turing/preparation_3dim_2.html
http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/16/ac/elemente/vlu/38_56_88.vlu.html
A face centered cubic unit cell has one atom at each corner and
one atom at each face center.

4.  Diamond cubic structure is obtained when two FCC sublattices
interpenetrates along the body diagonal by 1/4th cube edge.
http://www.materialsdesign.com/appnote
)ˆˆˆ(
4
zyx
a

a

5. http://www.materialsdesign.com/appnote
)ˆˆˆ(
4
zyx
a

a
 The space group of diamond is .
 There are eight carbon atoms at the corner, creating a cube.
 The six carbon atoms in the faces create an octahedron.
 The four internal carbon
atoms (black balls in figure)
lie at ¼ of the distance along
body diagonal forming a
tetrahedran.
mdF 3
C
C F C
C
C
C F C
C
F F F F
I I
I
I
The letters on the ball mean:
C – Corner atom
F – Face atom
I – Internal atom

6. Square on the right hand side indicates the base of the cube.
1/4
1/4
a

7. a
0 0
0 0
0
1/4
1/4
The number ‘0’ denotes the height above the base.
0 0 0 0
0

8. a
0 0 0
0
0
0 0
0 0
01/2 1/2
1/2
1/2
1/4
1/4
The number ‘0’ and fraction ‘½’ denote the height above the base.
1/2 1/2 1/2 1/2

9. a
0 0 0
0
0
0 0
0 0
01/2 1/2
1/2
1/2
1/4
1/4
1/4
1/4
The number ‘0’ and fractions ‘½’ and ‘¼’ denote the height above the base.
1/2 1/2 1/2 1/2
1/4 1/4

10. a
0 0 0
0
0
0 0
0 0
01/2 1/2
1/2
1/2
1/4
1/43/4
3/4
1/4
1/4
The number ‘0’ and fractions ‘½’ , ‘¼’ and ‘¾’ denote the height above the base.
1/2 1/2 1/2 1/2
1/4 1/4
3/43/4

11. Atomic Packing Factor
n = ? and r = ?
3
3
3
4
a
rn
cellunittheofVolume
atomonetheofVolumecellunitainpresentatomsofNumber
cellunittheofVolume
cellunitainatomsbyoccupiedvolumeTotal
APF





To solve APF of diamond structure, we need ‘n’ and ‘r’.

12. Atomic Packing Factor
nfcc = (1/8 x 8 corner atoms) + (1/2 x 6 face atoms)
= 1+3
= 4 atoms.
n = 4+4
= 8
r = ?
 There are atoms at all eight corners and all six faces.
 In addition to that there are 4 full atoms inside the unit cell.
Total number of atoms present in a unit cell.

13. Atomic Packing Factor
8
3
16
3
4
4)2(
2
2
222
a
r
a
r
rrXYBut



x
r z
a/4
a/4
a/4
y
16
3
48
844
222
222
222
2
aaa
ZYXZXY
aaa
XZ




















16
3
4
3
444
)ˆˆˆ(
4
2
2
222
a
XY
aaaa
YX
zyx
a
YXVector





















OR
)ˆˆˆ(
4
zyx
a

a
X
Y

14. Atomic Packing Factor
34.0
16
3
8
3
3
4
8
3
4
3
3
3
3



















a
a
a
rn
cellunittheofVolume
atomonetheofVolumecellunitainpresentatomsofNumber
cellunittheofVolume
cellunitainatomsbyoccupiedvolumeTotal
APF
%34 structurediamondoffactorpackingAtomic

15. please contact me via email for any further suggestions/comments.
Email: virendrave@gmail.com
Visit the below website for other topics
http://sciencebank.wordpress.com/