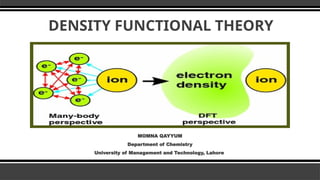
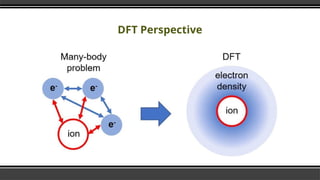
The document provides an overview of Density Functional Theory (DFT), a quantum-mechanical simulation method for calculating properties of atomic systems. It details the principles behind DFT, including the importance of electron density and the Hohenberg-Kohn theorem, which states that the ground state properties of a system can be determined from its electron density. The document also discusses practical applications of DFT in fields such as molecular dynamics, spectroscopy, and material science.

1. DENSITY FUNCTIONAL THEORY
MOMNA QAYYUM
Department of Chemistry
University of Management and Technology, Lahore

2. CONTENTS
▪ DFT
▪ Why DFT
▪ H 2O Molecule
▪ Electron Density
▪ Many Particle System
▪ Born-Oppenheimer Approximations
▪ Hohenburg Kohn Theorem
▪ References

3. Density Functional Theory
Density functional theory (DFT) is a quantum-mechanical atomistic
simulation method to compute a wide variety of properties of
almost any kind of atomic system: molecules, crystals, surfaces,
and even electronic devices when combined with non-equilibrium
Green's functions (NEGF).

4. DFT Perspective

5. Why DFT
Schrodinger Equation can be solved easily for one
electron system.
For multiple electronic system, it is very hard to solve
the Schrodinger equation.
▪ So we introduce some Approximations, one of them
is DFT
▪ Reduce electron-electron interactions.

6. H20 Molecule

7. H₂O Molecule Explained by DFT
▪ Density Functional Theory (DFT):
▪ Models the behavior of electrons in the H₂O molecule using electron density, not wave
functions.
▪ Efficiently predict molecular geometry, bond strengths, and electronic properties.
▪ Electron Density Distribution:
▪ DFT calculates the 3D electron density, showing how electrons are distributed around
the oxygen and hydrogen atoms.
▪ Highlights the polar nature of the H₂O molecule, with a higher electron density near
oxygen.

8. H₂O Geometry by DFT
▪ Bond Angle: ~104.5° (due to lone pair repulsion on oxygen).
▪ Bond Lengths: ~0.96 Å for O–H bonds (close to experimental
values).
▪ Potential Energy Surface (PES): DFT maps the energy changes as
the bond lengths and angles vary, providing insights into molecular
stability.

9. Electron Density

10. Electron Density
▪ Electron density significantly speeds up the calculation.
▪ Many body electronic wavefunction is a function of 3N variables the electron
density is only a function of x, y, z only three variables.
▪ The Hohenburg-Kohn theorem asserts that the density of any system
determines all ground-state properties of the system.
▪ In this case the total ground state energy of a many-electron system is a
functional of the density.

11. Many Particle System
▪ Find the ground state for a collection of atoms by
solving the Schrodinger equation
▪ Η Ψ({ri} {RI})= Ε Ψ ( {ri} {RI})
▪ So here we have a bunch of nuclei & bunch of
electron which makes a complicated equation to
solve.

12. Born-Oppenheimer Approximations
▪ According to this approximation:
▪ Mass of nuclei is very greater than mass of electrons
N>>>>e
▪ Thus nuclei are slow and electrons are fast.
▪ In other words we can write the Schrodinger wave
equation by separating the electronic and nuclei
terms.

13. Key Concepts of Born-Oppenheimer Approximations
1. Separation of Motion:
▪ Assumes that nuclei are much heavier than electrons, so their motion can be treated
separately.
▪ Electrons adjust instantly to the movement of nuclei.
2. Simplifies the Schrödinger Equation:
▪ Treats the electronic and nuclear wavefunctions independently, drastically reducing
computational complexity.
3. Energy Surface:
▪ The nuclei move on a potential energy surface defined by the electronic energy.

14. Why is This Important
▪ Simplifies Molecular Calculations: Reduces a complex multi-
particle system into more manageable parts.
▪ Basis for Quantum Chemistry: Enables understanding of chemical
bonding and molecular dynamics.
▪ Accurate Models: Provides realistic approximations for molecular
structure and spectroscopy.

15. Practical Applications
▪ Molecular Vibrations: Explains vibrational spectra by treating nuclei separately.
▪ Chemical Reactions: Helps map potential energy surfaces to understand reaction
pathways.
▪ Spectroscopy: Provides a framework for interpreting electronic, vibrational, and
rotational spectra.
▪ Molecular Dynamics Simulations: Simplifies calculations for simulating large
systems.
▪ Quantum Chemistry Software: Foundational principle behind tools like Gaussian and
VASP.

16. Hohenberg-kohn Theorem
▪ The Ground state energy E is the unique functional of Electron Density This foundational
concept in Density Functional Theory (DFT) has two key parts:
1. The Ground State Density Uniquely Defines All Properties
▪ The total energy and all properties of a quantum system can be determined entirely from the
electron density, not the many-electron wave function.
▪ This simplifies complex quantum calculations by reducing dimensions.
2. Existence of a Universal Energy Functional
▪ There exists a mathematical function that relates the energy of the system to the electron
density.
▪ The ground-state energy corresponds to the minimum of this energy functional.

17. Breaking Down the Hohenberg-kohn Theorem
1. Why Focus on Electron Density?
▪ Electron density tells us where electrons are most likely to be in a molecule or material.
▪ It’s much simpler than the many-body wave function but still contains all the essential
information.
2. Implications of the Theorem
▪ The energy and behavior of a system can be calculated without solving the complex
Schrödinger equation directly.
▪ This reduces the problem's complexity from many-electron interactions to just density
distribution.

18. Key Concepts of Hohenberg-kohn Theorem
▪ The ground-state electron density uniquely determines all properties of a quantum system
(e.g., energy, reactivity).
▪ Reduces complexity: Depends on 3 spatial variables, not the 3N variables of the wavefunction
(N = number of electrons).
▪ A mathematical function relates the energy of the system to the electron density.
▪ The ground-state energy corresponds to the minimum of this functional.
▪ The system is in its ground state (lowest energy).
▪ The relationship between energy and density is universal for all systems.

19. Why is This Important
▪ Simplifies Quantum Calculations: Reduces complexity from multi-electron wavefunctions to a
3-variable electron density.
▪ Foundation of DFT: Forms the basis for Density Functional Theory, a key tool in computational
chemistry and physics.
▪ Reduces Computational Cost: Enables accurate predictions for large systems with minimal
computational effort.
▪ Broad Applicability: Widely used in material science, catalysis, energy storage, and drug
discovery.
▪ Revolutionized Modern Chemistry: Transformed the study and design of molecules and
materials with efficient modeling techniques.

20. Practical Applications
▪ Material design: Predicts stability, conductivity, and magnetic properties
of materials.
▪ Drug Discovery: Models molecular interactions with biological targets.
▪ Catalysis: Optimizes catalysts for faster and greener reactions.
▪ Battery Development: Designs more efficient energy storage materials.
▪ Environmental Science: Models pollutant behavior and chemical
reactions in the atmosphere.

21. Hohenberg-kohn Theorem 1
▪ The Ground state energy E is the unique functional of
Electron Density
E = E 。 [po(r)]
▪ where p (r) represents the density function which itself is a
function of position (r).

22. ▪ The electron density that minimizes the energy of the
overall functional is the true ground state electron density:
E[p(r)]>E.[p.(r)]
Hohenberg-kohn Theorem 2

23. From Wave function to Electron Density
▪ So, we can separate the wave function for electron and nuclei
Ψ({ri} {RI})=ΨN {RI} Ψe {ri}
▪ DFT explains the electronic density.
▪ That reduce to N dimensional to 3 spatial dimension
▪ So electron density is only 3 dimensional

25. References
▪ Roienko, O., Lukin, V., Oliinyk, V., Djurović, I., & Simeunović, M. (2022). An Overview of the Adaptive
Robust DFT and its Applications. Technological Innovation in Engineering Research, 4, 68-89.
▪ Chakraborty, D., & Chattaraj, P. K. (2021). Conceptual density functional theory based electronic
structure principles. Chemical Science, 12(18), 6264-6279.
▪ Fiechter, M. R., & Richardson, J. O. (2024). Understanding the cavity Born–Oppenheimer
approximation. The Journal of Chemical Physics, 160(18).
▪ Liebert, J., & Schilling, C. (2023). An exact one-particle theory of bosonic excitations: from a
generalized Hohenberg–Kohn theorem to convexified N-representability. New Journal of
Physics, 25(1), 013009.

26. THANK YOU