The document discusses the design of pipe networks for water distribution. It describes various methods for analyzing pressure in distribution systems, including the equivalent pipe method, Hardy Cross method, and graphical method. The equivalent pipe method involves replacing a complex pipe system with a single hydraulically equivalent pipe. The document provides detailed steps for applying the equivalent pipe method to pipes placed in series and parallel. It also describes the Hardy Cross method which balances heads by iteratively correcting assumed pipe flows until the total head loss equals zero.

1. Design Of Pipe Network
Mr. M.H.Mota
Assistant Professor
SITCOE, Yadrav

2. Water distribution
• Water distribution systems are designed to
adequately satisfy the water requirement. The
performance of a distribution system can be
judged on the basis of pressure available on the
system for a specific rate of flow. The
distribution system consists of a network of
pipes with appurtenances.
• Pipes can be placed either parallel or in series.

3. Analysis of pressure in distribution
system
• Equivalent pipe method
• Hardy cross method
• Method of section and circle method
• Graphical method
• Newton-Rapson method

4. Basics of network analysis
• The flow entering in a junction or network must be
equal to the flow leaving the same.
• The algebraic sum of the pressure drops around a
closed loop must be zero i.e. there can be no
discontinuity in pressure.
Remember…..
• When the pipes are connected in series, the total head
loss is equal to the summation of the individual head
losses.
• When the pipes are laid parallel the head loss through
the parallel pipes(or set of pipes) will be the same.

5. Equivalent pipe method
• In this method a complex system of pipes is
replaced by single hydraulically equivalent
pipe.
Hydraulically equivalent pipe means ……
• It will have same capacity.(Q)
• It will have same amount of head loss.(hf)

6. • hf= (f.L.V2/2gD)
Where……
f……coeff. of friction(0.012).
L…… length of pipe line.
V…… velocity of flow.
D…… diameter of pipe.
Try to substitute V=Q/A in above equation.

7. • Hf = (f.L.V2/2gD)
= f.L.(Q/A)2/2gD
=f.L.Q2/2gDA2 A=∏/4 X D2
=16f.L.Q2/2g ∏ 2D5
Putting 16f/2g ∏ 2 as K (constant)
Now…
Hf = K.L.Q2/D5

8. • Consider a system consisting pipes placed in
series….system ABCD
• Has to be replaced by an equivalent pipe.
• Q will be same and total head loss from A to D
in system will be the head loss in equivalent
pipe.
Pipe Diameter length
AB D1 L1
BC D2 L2
CD D3 L3

9. • Hf = K.L.Q2/D5
• Let eq. pipe be have dia DE and length LE.
Now ……
• Hf(eq. pipe) = K. LE Q2/ DE
5
• Hf(AB) = K. L1.Q2/D1
5
• Hf(BC) = K. L2.Q2/D2
5
• Hf(CD) = K. L3.Q2/D3
5
• Hf(eq. pipe) =Hf(ABCD)
• K. LE Q2/ DE
5 = (K. L1.Q2/D1
5 )+ (K. L2.Q2/D2
5 )+
(K. L3.Q2/D3
5)
• K. LE Q2/ DE
5 = (K. L1.Q2/D1
5 )+ (K. L2.Q2/D2
5 )+
(K. L3.Q2/D3
5)

10. • K. LE Q2/ DE
5 = (K. L1.Q2/D1
5 )+ (K.
L2.Q2/D2
5 )+ (K. L3.Q2/D3
5)
• LE / DE
5 = (L1/D1
5 )+ (L2/D2
5 )+(L3/D3
5)
• Determine the equivalent length of 30cm dia
pipe for network of pipes placed in parallel.
Pipe Length(m) Diameter(cm)
AB 300 40
BC 400 30
CD 500 20

11. • LE / DE
5 = (L1/D1
5 )+ (L2/D2
5 )+(L3/D3
5)
• LE / 0.30 5 =(300/0.45)+(400/0.35)+(500/0.25)
• LE = 4268m.

12. Pipes placed parallel
A B
C D

13. • Q = Q1 + Q2
Pipe Length Diameter Flow
AB L1 D1 Q1
BD L2 D2 Q1
AC L3 D3 Q2
AD L4 D4 Q2

14. The length of equivalent pipe for pipe AB and BD
• LE1 / DE
5 = (L1/D1
5 )+ (L2/D2
5 )
The length of equivalent pipe for pipe AC and CD
• LE2 / DE
5 = (L3/D3
5 )+ (L4/D4
5 )
• Similarly for the pipes placed parallel i.e. ABD and
ACD, head loss will be same.
Hf(ABD)= Hf(ACD)
(Head loss through pipes= Hf = K.L.Q2/D5)

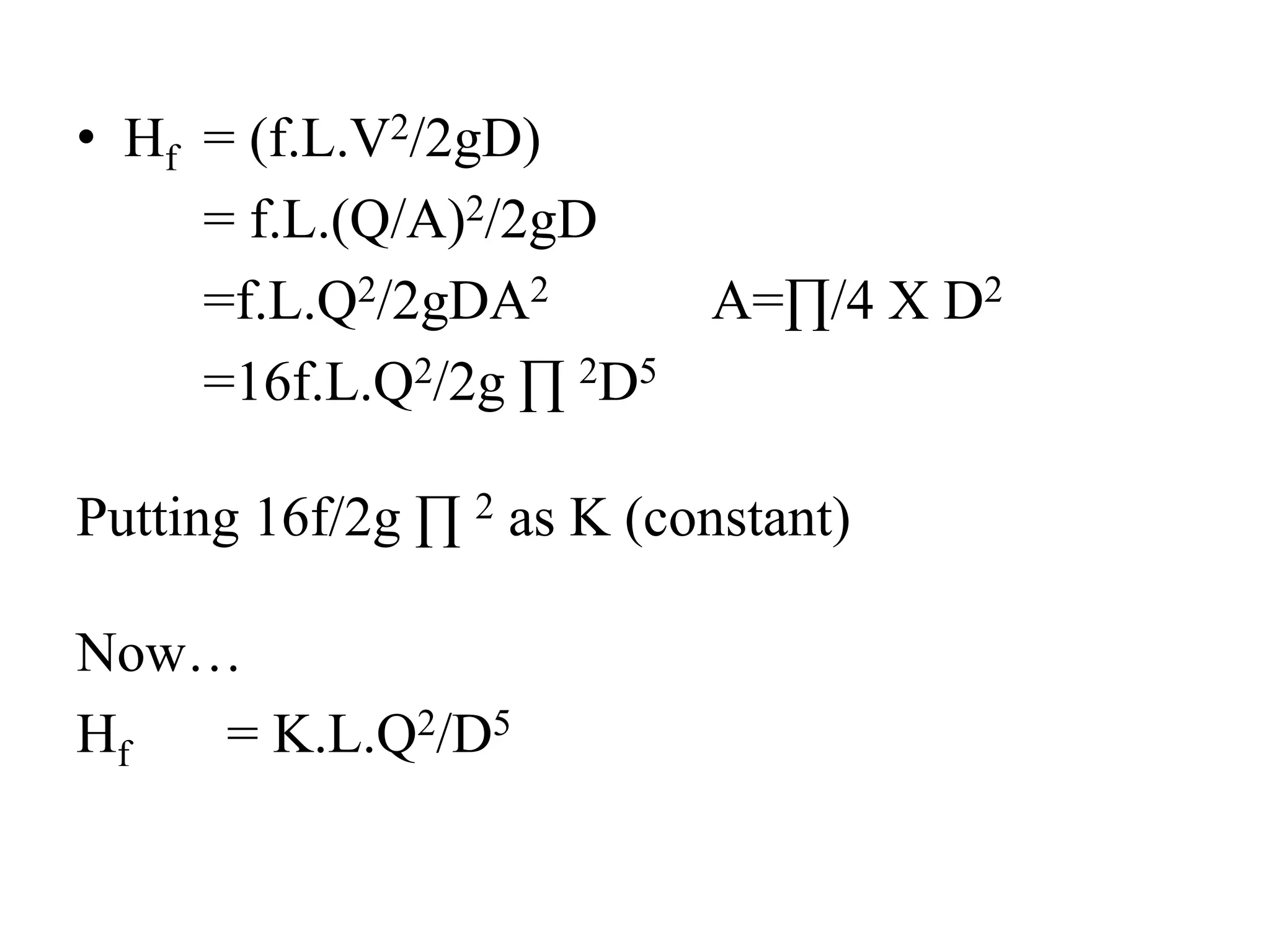
15. • Hf(ABD)= (K.L1Q1
2/D1
5 )+ (K.L2.Q1
2/D2
5)
• Hf(ACD)= (K.L3Q2
2/D3
5 )+ (K.L4.Q2
2/D4
5)
Now…
(K.L1Q1
2/D1
5 )+ (K.L2.Q1
2/D2
5) = (K.L3Q2
2/D3
5 )+ (K.L4.Q2
2/D4
5)
(K.L1Q1
2/D1
5 )+ (K.L2.Q1
2/D2
5) = (K.L3Q2
2/D3
5 )+ (K.L4.Q2
2/D4
5)
(L1Q1
2/D1
5 )+ (L2.Q1
2/D2
5) = (L3Q2
2/D3
5 )+ (L4.Q2
2/D4
5)
Q1
2 [(L1/D1
5 )+ (L2/D2
5)] = Q2
2 [(L3/D3
5 )+ (L4/D4
5)]
Q1
2 / Q2
2 = [(L3/D3
5 )+ (L4/D4
5)] / [(L1/D1
5 )+ (L2/D2
5)]
Q1 / Q2 = sqrt {[(L3/D3
5 )+ (L4/D4
5)] / [(L1/D1
5 )+ (L2/D2
5)] }
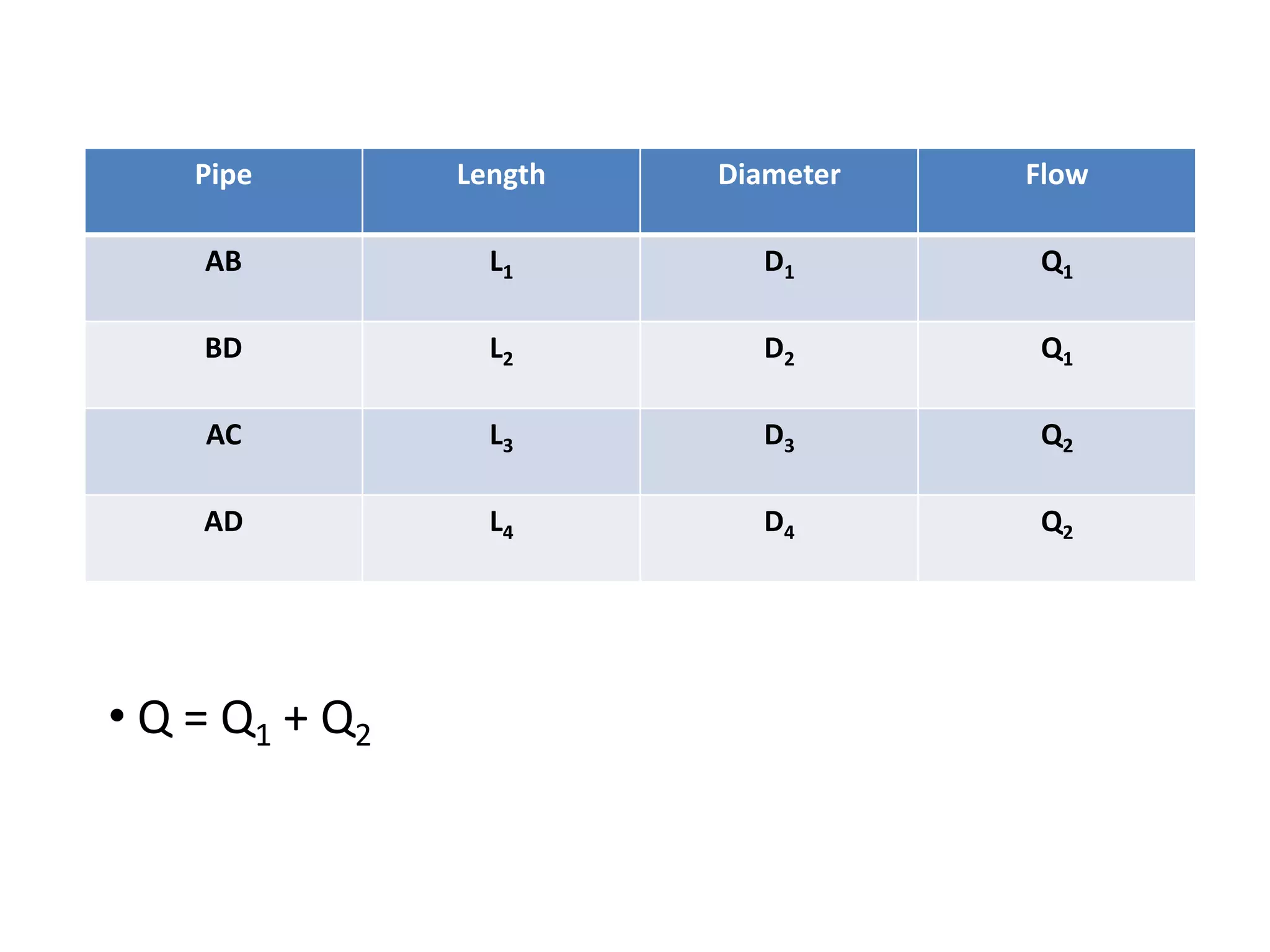
Q1 / Q2 = A or Q1 = A.Q2 or Q=Q2 (A+1)

16. Now if LE and DE are the properties of equivalent
pipe replacing whole network it should able to
carry the total flow ‘Q’ and should have same head
loss i.e. Hf(ABD) or Hf(ACD)
K.LEQ2/DE
5 =(K.L3Q2
2/D3
5 )+ (K.L4.Q2
2/D4
5)
LEQ2/DE
5 = (L3Q2
2/D3
5 )+ (L4.Q2
2/D4
5)
As ……Q=Q2 (A+1)
LE[Q2 (A+1)]2/DE
5 = (L3Q2
2/D3
5 )+ (L4.Q2
2/D4
5)
LE /DE
5= [(L3Q2
2/D3
5)+(L4.Q2
2/D4
5)] / (A+1)2
LE = DE
5 .[(L3Q2
2/D3
5)+(L4.Q2
2/D4
5)] / (A+1)2

17. • Important…..
All above derivations are based on Darcy’s formula.
If Hazen Williams formula has to be used the
equivalent length can be calculated using
following modifications……
For pipes in series……
LE / DE
4.87 = (L1/D1
4.87 )+ (L2/D2
4.87 )+(L3/D3
4.87)
For parallel pipes……
LE /DE
4.87= [(L3Q2
1.85/D3
4.87)+(L4.Q2
1.85/D4
4.87)] / (A+1)2

18. Hardy Cross method (balancing heads)
Basic assumptions……
1. In each separate pipe or element comprising the
system, there will be a relation between the head
loss in the element and the quantity of water
flowing in it. i.e. Hf = K.Qn
• Hf =16f.L.Q2/2g ∏ 2D5
• Hf = K.Q2…… for Darcy’s formula
K……16f.L/2g ∏ 2D5 (will have a constant value)
• Hf = K.Q1.85…… for Hazen Williams formula
K……10.62 L/C1.85.D4.87 (will have a constant
value)

19. 2. At each junction the algebraic sum of the
quantities of water entering and leaving the
junction is zero. i.e.ΣQ=0.
3. In any closed path the algebraic sum of the
head loss is zero. i.e.ΣHf=0.

20. Steps to solve the network using hardy cross
method (balancing heads by correcting heads)
Consider a network of following properties…
• Total flow entering in network(at node A)…Q m3/s
• Demand at nodes QB,QC and QD m3/s respectively.
• Therefore Q= QB+ QC +QD
• Details of dimensions and flow…
Pipe Length(m) Diameter(cm) Assumed
Flow(m3/s)
AB LAB DAB Q1
BC LBC DBC Q2
CD LCD DCD Q3
DA LDA DDA Q4

21. • Step 1. assume the flow considering continuity.
• Step 2. calculate the head loss in each pipe using either
Darcy’s or HW formula.
Hf = K.L.Q2/D5…… Darcy’s formula
Hf = K.L.Q1.85/D4.87 …… HW formula
• Step 3. Assign +ve sign for clockwise flow and
associated head loss and Assign -ve sign for anti-
clockwise flow and associated head loss.
Now……(Using HW formula)
• HAB = K.LAB.Q1
1.85/DAB
4.87 (+ve)
• HBC = K.LBC.Q2
1.85/DBC
4.87 (+ve)
• HCD = K.LCD.Q3
1.85/DCD
4.87 (-ve)
• HDA = K.LDA.Q4
1.85/DDA
4.87 (-ve)

22. • Step 4.Calculate the total head loss by adding all.
• Σ HL = HAB (+ve) + HBC (+ve) + HCD(-
ve) +HDA (-ve)
• Σ HL = HAB + HBC - HCD-HAD
HL must be zero.(may not be the case in 1st trial.)
• Step 5.Calculate the correction to be applied in each
assumed flow using formula……
• ΔQ=- ΣHL/(n ΣHf/Q)
n……2 for Darcy's formula and 1.85 for HW
formula.
• Step 6. add this correction with it’s sign to assumed
flow with it’s own sign.

23. • Step 6. add this correction with it’s sign to
assumed flow with it’s own sign.
• Suppose ΔQ is –ve value, then modified flow
in each pipe will be calculated as……
QAB=(+ve) Q1- ΔQ
QBC=(+ve) Q2 -ΔQ
QCD=(-ve) Q3-ΔQ
QAD=(-ve) Q4 -ΔQ
• Step 7. Repeat the steps(1 to 6)with modified
flow until the Σ HL comes to zero.

24. References:
• Environmental Engineering. Vol. I …. S K Garg
• Water supply Engineering….. B C Punmia.

25. •Thank you.