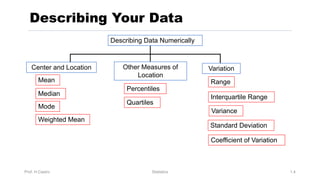
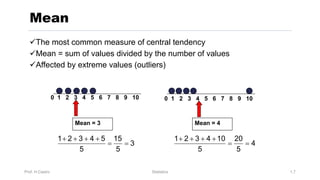
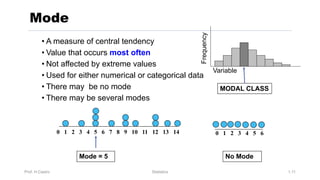
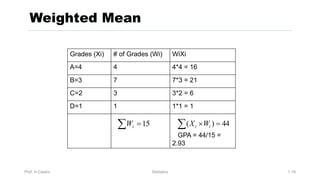
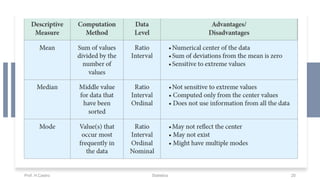
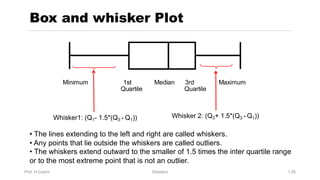
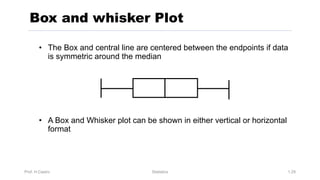
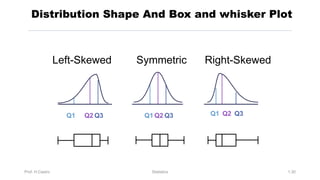
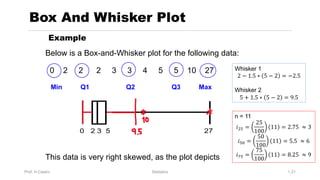
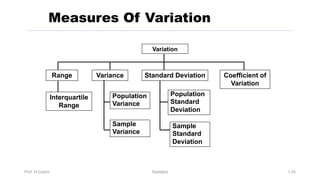
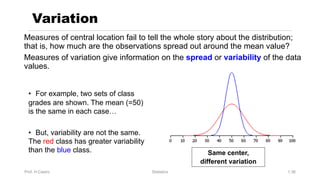
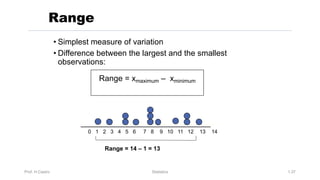
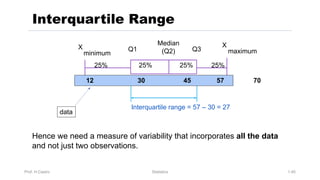
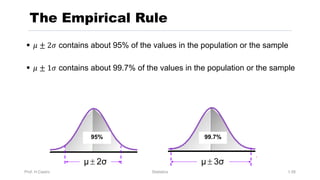
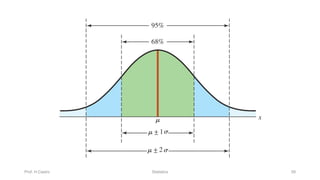
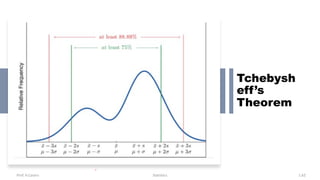
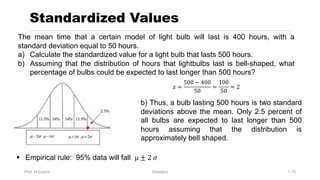
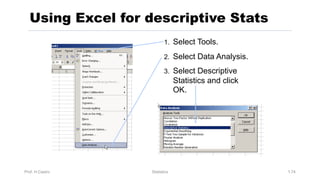
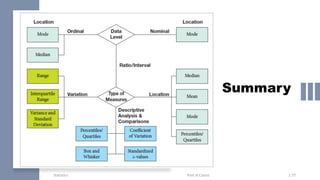
Chapter 3 focuses on numerical measures to describe data, including central tendency (mean, median, mode), variation (variance, standard deviation, range), and distribution shape. It explains how these measures differ between population parameters and sample statistics, as well as their significance in data analysis. The chapter also highlights the impact of outliers and the use of box-and-whisker plots and percentiles to visualize data distribution.