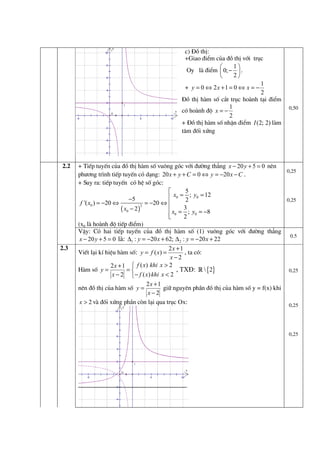
Tài liệu là đề kiểm tra học kỳ của môn Toán lớp 12 năm học 2013-2014, bao gồm các bài tập về đạo hàm, cực trị, và phương trình của đường thẳng. Các bài tập yêu cầu học sinh tính toán, viết phương trình và tìm điểm giao nhau của các đồ thị trong không gian. Đề bài cũng có phần hướng dẫn chi tiết về cách thực hiện các phép toán và phân tích hình học.

1. kiÓm tra häc kú I n¨m häc 2013-2014
Së Gi¸o dôc vµ ®µo t¹o
M«n: TO¸N - Líp 12
Thêi gian lµm bµi: 90 phót
§Ò chÝnh thøc
Bµi 1: (2,25 ®iÓm)
1. TÝnh vi ph©n cña mçi hµm sè sau:
a) y = e
2x
cos x ;
b) y = cotg 2 x .
2. T×m c¸c ®iÓm cùc trÞ cña hµm sè y =
4
3
(1 ®)
2
x 2 x 3x
.
−
−
4
3
2
(1,25 ®)
Bµi 2: (3,75 ®iÓm)
Cho hµm sè y =
2x + 1
x−2
(1)
1. Kh¶o s¸t hµm sè (1).
(2 ®)
2. ViÕt ph−¬ng tr×nh c¸c tiÕp tuyÕn cña ®å thÞ hµm sè (1) vu«ng gãc víi
®−êng th¼ng x − 20 y + 5 = 0 .
(1 ®)
3. Dùa vµo ®å thÞ cña hµm sè (1), vÏ ®å thÞ cña hµm sè: y =
2x + 1
.
x−2
(0,75 ®)
Bµi 3: (2,5 ®iÓm)
Trong mÆt ph¼ng víi hÖ to¹ ®é Oxy, cho hai ®−êng th¼ng d1 : x + 2 y + 4 = 0 ;
d 2 : 2 x − 3 y − 13 = 0 vµ ®iÓm I ( −3; 7 )
(0,5 ®)
1. T×m to¹ ®é giao ®iÓm cña 2 ®−êng th¼ng d1 vµ d2 .
2. ViÕt ph−¬ng tr×nh ®−êng th¼ng ∆ ®i qua giao ®iÓm cña 2 ®−êng th¼ng d1 ,
(1 ®)
d 2 vµ song song víi ®−êng th¼ng 4 x − 3 y + 5 = 0 .
3. ViÕt ph−¬ng tr×nh ®−êng trßn t©m I vµ tiÕp xóc víi ®−êng th¼ng ∆ . (1 ®)
Bµi 4: (1,5 ®iÓm)
Trong mÆt ph¼ng víi hÖ to¹ ®é Oxy:
1. ViÕt ph−¬ng tr×nh chÝnh t¾c cña elÝp (E) cã ®é dµi trôc bÐ lµ 8 vµ t©m sai
3
e= .
5
(1 ®)
2. T×m to¹ ®é c¸c giao ®iÓm cña elÝp (E) vµ ®−êng th¼ng ®i qua 2 ®iÓm
(0,5 ®)
M ( 0; − 1) , N (1; 1) .
HÕt

2. ĐÁP ÁN
Bµi
ý
Néi dung
§iÓm
1
2.25
1.1 a) dy = y ' dx = e
2x
( 2 cos x − sin x ) dx
0.5
1 
2 cot gxdx

b) dy = y ' dx = 2 cot gx  − 2  dx = −
sin 2 x
 sin x 
1.2 TX§: R;
y ' = x 3 − 2 x 2 − 3 x = x ( x 2 − 2 x − 3)
y ' = 0 ⇔ x1 = 0; x2 = −1; x3 = 3
0.5
0..25
0.25
y " = 3x 2 − 4 x − 3 ; y " ( 0 ) = −3 < 0; y "(−1) = 4 > 0; y " ( 3) = 12 > 0
0.25
¸p dông dÊu hiÖu ®ñ thø 2: Hµm sè ®¹t cùc ®¹i t¹i x1 = 0; yC§ = 0; ®¹t cùc tiÓu
7
45
vµ x3 = 3; yCT = −
t¹i 2 ®iÓm x2 = −1; yCT = −
12
4
0.50
2
3.75
2.1 (2,0 ®iÓm)
2x + 1
(1)
x−2
a) TËp x¸c ®Þnh: D = R {2} .
b) Sù biÕn thiªn:
−5
y'=
< 0, ∀x ∈ D . Suy ra: Hµm sè lu«n lu«n ®ång biÕn trªn tõng
2
( x − 2)
kho¶ng x¸c ®Þnh cña nã.
b) Giíi h¹n vµ tiÖm cËn: lim y = ∞ ; lim y = 2
Kh¶o s¸t hµm sè y =
x→2
x →∞
Nªn ®å thÞ cña (1) cã tiÖm cËn ®øng lµ ®−êng th¼ng x = 2 vµ tiÖm cËn ngang lµ
®−êng th¼ng y = 2 .
+ B¶ng biÕn thiªn
x −∞
2
+∞
−
y'
+∞
2
y
−∞
−
0.50
0.50
0.50
2

3. c) §å thÞ:
+Giao ®iÓm cña ®å thÞ víi trôc
1

Oy lµ ®iÓm  0; −  .
2

1
+ y = 0 ⇔ 2x +1 = 0 ⇔ x = −
2
§å thÞ hµm sè c¾t trôc hoµnh t¹i ®iÓm
1
cã hoµnh ®é x = −
2
+ §å thÞ hµm sè nhËn ®iÓm I (2; 2) lµm
t©m ®èi xøng
2.2
2.3
0,50
+ TiÕp tuyÕn cña ®å thÞ hµm sè vu«ng gãc víi ®−êng th¼ng x − 20 y + 5 = 0 nªn
0,25
ph−¬ng tr×nh tiÕp tuyÕn cã d¹ng: 20 x + y + C = 0 ⇔ y = −20 x − C .
+ Suy ra: tiÕp tuyÕn cã hÖ sè gãc:
5

 x0 = 2 ; y0 = 12
−5
0,25
f '( x0 ) = −20 ⇔
= −20 ⇔ 
2
( x0 − 2 )
 x = 3 ; y = −8
 0 2 0

(x0 lµ hoµnh ®é tiÕp ®iÓm)
VËy: Cã hai tiÕp tuyÕn cña ®å thÞ hµm sè (1) vu«ng gãc víi ®−êng th¼ng
0.5
x − 20 y + 5 = 0 lµ: ∆1 : y = −20 x + 62; ∆ 2 : y = −20 x + 22
2x +1
ViÕt l¹i kÝ hiÖu hµm sè: y = f ( x) =
, ta cã:
x−2
2 x + 1  f ( x) khi x > 2
Hµm sè y =
, TXĐ: R {2}
=
0,25
x − 2  − f ( x) khi x < 2
2x + 1
nªn ®å thÞ cña hµm sè y =
gi÷ nguyªn phÇn ®å thÞ cña hµm sè y = f(x) khi
x−2
x > 2 vµ ®èi xøng phÇn cßn l¹i qua trôc Ox:
0,25
0,25

4. 2,5
3
3.1
3.2
+ Täa ®é giao ®iÓm cña 2 ®−êng th¼ng d1 : x + 2 y + 4 = 0 ; d 2 : 2 x − 3 y − 13 = 0 lµ
 x + 2 y = −4
nghiÖm cña hÖ ph−¬ng tr×nh: 
,
2 x − 3 y = 13
+ Gi¶i hÖ pt ta ®−îc: x = 2; y = −3 . Do ®ã giao ®iÓm cña 2 ®−êng th¼ng d1 vµ d2
lµ M (2; − 3)
§−êng th¼ng ∆ song song víi ®−êng th¼ng 4 x − 3 y + 5 = 0 , nªn ph−¬ng tr×nh cã
d¹ng 4 x − 3 y + C = 0 ( C ≠ 5 )
§−êng th¼ng ∆ ®i qua giao ®iÓm cña d1 vµ d2 nªn:
4 ⋅ 2 − 3 ( −3) + C = 0 ⇔ C = −17 .
VËy ph−¬ng tr×nh ®−êng th¼ng ∆ lµ 4 x − 3 y − 17 = 0
3.3
0.25
0,25
0.50
0.25
0,25
+ §−êng trßn t©m I ( −3; 7 ) vµ tiÕp xóc víi ®−êng th¼ng ∆ , nªn cã b¸n kÝnh:
R = d ( I , ∆) =
4 ( −3) − 3 ⋅ 7 − 17
0,50
= 10
5
2
2
+ VËy ph−¬ng tr×nh ®−êng trßn cÇn t×m lµ: ( x + 3) + ( y − 7 ) = 100
4
0.50
1,5
4.1
+ Theo gi¶ thiÕt:
Elip cã ®é dµi nöa trôc bÐ b = 4; t©m sai e =
c 3
3a
= ⇔c=
a 5
5
9a 2 16a 2
=
⇔ a 2 = 25 ⇔ a = 5
25
25
x2 y 2
+ Suy ra ph−¬ng tr×nh chÝnh t¾c cña (E) lµ:
+
=1
25 16
 x=t
Ph−¬ng tr×nh tham sè cña (MN): 
 y = −1 + 2t
HÖ ph−¬ng tr×nh cho to¹ ®é giao ®iÓm cña (MN) vµ (E) lµ:
x=t

x=t

 y = −1 + 2t


⇔
y = −1 + 2t
 2
2
( 2t − 1) = 1 116t 2 − 100t − 375 = 0
t

 25 + 16

+ Mµ b 2 = a 2 − c 2 ⇔ 16 = a 2 −
4.2
25 − 10 115
25 + 10 115
.
; t2 =
58
58
Suy ra 2 giao ®iÓm cña (MN) vµ (E) lµ:
 25 − 10 115 −4 − 10 115 
 25 − 10 115 −4 + 10 115 
M1 
;
;
, M2 





58
29
58
29




0,25
0,50
0,25
0.25
+Gi¶i hÖ ta ®−îc: t1 =
0,25