Arrays are data structures that store a collection of data values of the same type in consecutive memory locations that can be individually referenced by their numeric index. Different representations of arrays are possible including using a single block of memory or a collection of elements. Common operations on arrays include retrieving or storing elements by their index and traversing the entire array sequentially.

1. Arrays

2. Arrays
Array: a set of index and value
data structure
For each index, there is a value associated with
that index.
representation (possible)
implemented by using consecutive memory.
Example: int list[5]: list[0], …, list[4] each contains
an integer
0 1 2 3 4
List

3. class GeneralArray {
// objects: A set of pairs < index, value> where for each value of index in IndexSet
there is a value of type float. IndexSet is a finite ordered set of one or more
dimensions,
// for example, {0, …, n-1} for one dimension, {(0, 0), (0, 1), (0, 2),(1, 0), (1, 1), (1, 2),
(2, 0),
// (2, 1), (2, 2)} for two dimensions, etc.
public:
GeneralArray(int j; RangeList list, float initValue = defatultValue);
// The constructor GeneralArray creates a j dimensional array of floats; the range
of
// the kth dimension is given by the kth element of list. For each index i in the
index
// set, insert <i, initValue> into the array.
float Retrieve(index i);
// if (i is in the index set of the array) return the float associated with i
// in the array; else signal an error
void Store(index i, float x);
// if (i is in the index set of the array) delete any pair of the form <i, y> present
// in the array and insert the new pair <i, x>; else signal an error.
}; // end of GeneralArray

4. Arrays in C
int list[5], *plist[5];
list[5]: five integers
list[0], list[1], list[2], list[3], list[4]
*plist[5]: five pointers to integers
plist[0], plist[1], plist[2], plist[3], plist[4]
0 1 2 3 4
Plist
0 1 2 3 4
List

5. Arrays in C (cont’d)
implementation of 1-D array
list[0] base address = α
list[1] α + sizeof(int)
list[2] α + 2*sizeof(int)
list[3] α + 3*sizeof(int)
list[4] α + 4*size(int)
Compare int *list1 and int list2[5] in C.
Same: list1 and list2 are pointers.
Difference: list2 reserves five locations.
Notations:
list2 - a pointer to list2[0]
(list2 + i) - a pointer to list2[i] (&list2[i])
*(list2 + i) - list2[i]

6. Example: 1-dimension array addressing
int one[] = {0, 1, 2, 3, 4};
Goal: print out address and value
void print1(int *ptr, int rows)
{
/* print out a one-dimensional array using a pointer */
int i;
printf(“Address Contentsn”);
for (i=0; i < rows; i++)
printf(“%8u%5dn”, ptr+i, *(ptr+i));
printf(“n”);
}

7. Address Contents
1228 0
1230 1
1232 2
1234 3
1236 4
call print1(&one[0], 5)

8. Structures (records)
struct {
char name[10];
int age;
float salary;
} person;
strcpy(person.name, “james”);
person.age=10;
person.salary=35000;

9. Create structure data type
typedef struct human_being {
char name[10];
int age;
float salary;
};
or
typedef struct {
char name[10];
int age;
float salary
} human_being;
human_being person1, person2;

10. Unions
Similar to struct, but only one field is active.
Example: Add fields for male and female.
typedef struct sex_type {
enum tag_field {female, male} sex;
union {
int children;
int beard;
} u;
};
typedef struct human_being {
char name[10];
int age;
float salary;
date dob;
sex_type sex_info;
}
human_being person1, person2;
person1.sex_info.sex=male;
person1.sex_info.u.beard=FALSE;

11. Self-Referential Structures
One or more of its components is a pointer to itself.
typedef struct list {
char data;
list *link;
}
list item1, item2, item3;
item1.data=‘a’;
item2.data=‘b’;
item3.data=‘c’;
item1.link=item2.link=item3.link=NULL;
malloc: obtain a node
Construct a list with three nodes
item1.link=&item2;
item2.link=&item3;
a b c

12. Ordered List Examples
(MONDAY, TUEDSAY, WEDNESDAY,
THURSDAY, FRIDAY, SATURDAYY,
SUNDAY)
(2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King,
Ace)
(1941, 1942, 1943, 1944, 1945)
(a1, a2, a3, …, an-1, an)
ordered (linear) list: (item1, item2, item3, …, itemn)

13. Operations on Ordered List
(1) Find the length, n , of the list.
(2) Read the items from left to right (or right to left).
(3) Retrieve the i’th element.
(4) Store a new value into the i’th position.
(5) Insert a new element at the position i , causing
elements numbered i, i+1, …, n to become numbered
i+1, i+2, …, n+1
(6) Delete the element at position i , causing elements
numbered i+1, …, n to become numbered i, i+1, …,
n-1 array (sequential mapping)? (1)~(4) O (5)~(6) X

14. ne
n
e
xaxaxp ++= ...)( 1
1
Polynomials A(X)=3X20+2X5+4, B(X)=X4+10X3+3X2+1
class polynomial {
// objects: a set of ordered pairs of <ei, ai>
//where ai Coefficient and ei Exponent
// We assume that Exponent consists of integers ≥ 0
public:
Polynomial();
// return the polynomial p(x) = 0
int operator!();
// if *this is the zero polynomial, return 1; else return 0;
Coefficient Coef(Exponent e);
// return the coefficient of e in *this
Exponent LeadExp();
// return the largest exponent in *this
Polynomial Add(Polynomial poly);
// return the sum of the polynomials *this and poly
Polynomial Mult(Polynomial poly);
// return the product of the polynomials *this and poly
float Eval(float f);
// Evaluate the polynomial *this at f and return the result
}; end of Polynomial

15. Polynomial Representation 1
0 1 2 3 4
CoeffArray 1 0 3 10 1
x4+10x3+3x2+1
private:
int degree; // degree ≤ MaxDegree
float coef [MaxDegree + 1];

16. /* d =a + b, where a, b, and d are polynomials */
d = Zero( )
while (! IsZero(a) && ! IsZero(b)) do {
switch COMPARE (Lead_Exp(a), Lead_Exp(b)) {
case -1: d =
Attach(d, Coef (b, Lead_Exp(b)), Lead_Exp(b));
b = Remove(b, Lead_Exp(b));
break;
case 0: sum = Coef (a, Lead_Exp (a)) + Coef ( b, Lead_Exp(b));
if (sum) {
Attach (d, sum, Lead_Exp(a));
a = Remove(a , Lead_Exp(a));
b = Remove(b , Lead_Exp(b));
}
break;
case 1: d =
Attach(d, Coef (a, Lead_Exp(a)), Lead_Exp(a));
a = Remove(a, Lead_Exp(a));
}
}
insert any remaining terms of a or b into d
Polynomial Addition

17. use one global array to store all polynomials
A.Start A.Finish B.Start B.Finish free
coef 2 1 1 10 3 1
exp 1000 0 4 3 2 0
0 1 2 3 4 5 6
A(X)=2X1000+1
B(X)=X4+10X3+3X2+1
specification representation
poly <start, finish>
A <0,1>
B <2,5>
Polynomial Representation 3

18. storage requirements: start, finish, 2*(finish-start+1)
nonsparse: twice as much as (1)
when all the items are nonzero
class term {
friend Polynomial;
private:
float coef; // coefficient
int exp; // exponent
};
class Polynomial; // forward delcaration
{ private:
static term termArray[MaxTerms];
static int free;
int Start, Finish;
}
term Polynomial:: termArray[MaxTerms];
int Polynomial::free = 0; // location of next free location in temArray

19. Polynomial Polynomial:: Add(Polynomial B)
// return the sum of A(x) ( in *this) and B(x)
{
Polynomial C; int a = Start; int b = B.Start; C.Start = free; float c;
while ((a <= Finish) && (b <= B.Finish))
switch (compare(termArray[a].exp, termArray[b].exp)) {
case ‘=‘:
c = termArray[a].coef +termArray[b].coef;
if ( c ) NewTerm(c, termArray[a].exp);
a++; b++;
break;
case ‘<‘:
NewTerm(termArray[b].coef, termArray[b].exp);
b++;
case ‘>’:
NewTerm(termArray[a].coef, termArray[a].exp);
a++;
} // end of switch and while
// add in remaining terms of A(x)
for (; a<= Finish; a++)
NewTerm(termArray[a].coef, termArray[a].exp);
// add in remaining terms of B(x)
for (; b<= B.Finish; b++)
NewTerm(termArray[b].coef, termArray[b].exp);
C.Finish = free – 1;
return C;
} // end of Add
Analysis: O(n+m) where n (m) is
the number of nonzeros in A(B).

20. Adding a new Term
void Polynomial::NewTerm(float c, int e)
// Add a new term to C(x)
{
if (free >= MaxTerms) {
cerr << “Too many terms in polynomials”<< endl;
exit();
}
termArray[free].coef = c;
termArray[free].exp = e;
free++;
} // end of NewTerm

21. Disadvantages of Representing Polynomials
by Arrays
What should we do when free is going to exceed
MaxTerms?
– Either quit or reused the space of unused polynomials.
But costly.
If use a single array of terms for each polynomial,
it may alleviate the above issue but it penalizes
the performance of the program due to the need of
knowing the size of a polynomial beforehand.

22. (a) (b)
Figure 2.2:Two matrices
8/36
6*65*3
15/15
Sparse Matrix
sparse matrix
data structure?
−
−
−
472748
9812
1164109
2826
4327
−
−
0002800
0000091
000000
006000
0003110
150220015

23. class SparseMatrix
// objects: A set of triples, <row, column, value>, where row and
column are integers and form a unique combinations; value is also
an integer.
public:
SparseMatrix(int MaxRow, int MaxCol);
// the constructor function creates a SparseMatrix that can
hold up to
// MaxInterms = MaxRow x MaxCol and whose maximum
row size is MaxRow
// and whose maximum column size is MaxCol
SparseMatrix Transpose();
// returns the SparseMatrix obtained by interchanging the
row and column value
// of every triple in *this
SPARSE MATRIX ABSTRACT DATA TYPE

24. SparseMatrix Add(SparseMatrix b);
// if the dimensions of a (*this) and b are the same, then the matrix
produced by adding corresponding items, namely those with identical
row and column values is returned
// else error.
SparseMatrix Multiply(SparseMatrix b);
// if number of columns in a (*this) equals number of rows in b then
the matrix d produced by multiplying a by b according to the formula
d[i][j] = Σ(a[i][k] . b[k][j]), where d[i][j] is the (i, j)th element, is returned.
k ranges from 0 to the number of columns in a – 1
// else error

25. Sparse Matrix Representation
Use triple <row, column, value>
Store triples row by row
For all triples within a row, their column
indices are in ascending order.
Must know the number of rows and
columns and the number of nonzero
elements

26. row col value row col value
a[0] 0 0 15 b[0] 0 0 15
[1] 0 3 22 [1] 0 4 91
[2] 0 5 -15 [2] 1 1 11
[3] 1 1 11 [3] 2 1 3
[4] 1 2 3 [4] 2 5 28
[5] 2 3 -6 [5] 3 0 22
[6] 4 0 91 [6] 3 2 -6
[7] 5 2 28 [7] 5 0 -15
(a) (b)
(1) Represented by a two-dimensional array.
Sparse matrix wastes space.
(2) Each element is characterized by <row, col, value>.
row, column in ascending order
transpose

27. class SparseMatrix; // forward declaration
class MatrixTerm {
friend class SparseMatrix
private:
int row, col, value;
};
In class SparseMatrix:
private:
int Rows, Cols, Terms;
MatrixTerm smArray[MaxTerms];

28. Transpose a Matrix
(1) for each row i
take element <i, j, value> and store it
in element <j, i, value> of the transpose.
difficulty: where to put <j, i, value>
(0, 0, 15) ====> (0, 0, 15)
(0, 3, 22) ====> (3, 0, 22)
(0, 5, -15) ====> (5, 0, -15)
(1, 1, 11) ====> (1, 1, 11)
Move elements down very often.
(2) For all elements in column j,
place element <i, j, value> in element <j, i, value>
row

29. SparseMatrix SparseMatrix::Transpose()
// return the transpose of a (*this)
{
SparseMatrix b;
b.Rows = Cols; // rows in b = columns in a
b.Cols = Rows; // columns in b = rows in a
b.Terms = Terms; // terms in b = terms in a
if (Terms > 0) // nonzero matrix
{
int CurrentB = 0;
for (int c = 0; c < Cols; c++) // transpose by columns
for (int i = 0; i < Terms; i++)
// find elements in column c
if (smArray[i].col == c) {
b.smArray[CurrentB].row = c;
b.smArray[CurrentB].col = smArray[i].row;
b.smArray[CurrentB].value = smArray[i].value;
CurrentB++;
}
} // end of if (Terms > 0)
return b;
} // end of transpose
Time Complexity O(terms*cols)
column
term element
matrix
0
c = column
b
column assignment

30. Discussion: compared with 2-D array representation
O(columns*terms) vs. O(columns*rows)
terms--> columns * rows when nonsparse
O(columns*columns*rows)
Problem: Scan the array “columns” times.
Solution:
Determine the number of elements in each column of
the original matrix.
Determine the starting positions of each row in the
transpose matrix.

31. index [0] [1] [2] [3] [4] [5]
RowSize = 3 2 1 0 1 1
RowStart = 0 3 5 6 6 7
row col value row col value
a[0] 0 0 15 b[0] 0 0 15
[1] 0 3 22 [1] 0 4 91
[2] 0 5 -15 [2] 1 1 11
[3] 1 1 11 [3] 2 1 3
[4] 1 2 3 [4] 2 5 28
[5] 2 3 -6 [5] 3 0 22
[6] 4 0 91 [6] 3 2 -6
[7] 5 2 28 [7] 5 0 -15
ba
row
start+size

32. Fast Matrix Transposing
SparseMatrix SparseMatrix::Transpose()
// The transpose of a(*this) is placed in b and is found in Q(terms + columns) time.
{
int *Rows = new int[Cols];
int *RowStart = new int[Cols];
SparseMatrix b;
b.Rows = Cols; b.Cols = Rows; b.Terms = Terms;
int i;
if (Terms > 0) // nonzero matrix
{
// compute RowSize[i] = number of terms in row i of b
for ( i = 0; i < Cols; i++) RowSize[i] = 0; // Initialize
for ( i = 0; i < Terms; I++) RowSize[smArray[i].col]++;
// RowStart[i] = starting position of row i in b
RowStart[0] = 0;
for (i = 1; i < Cols; i++) RowStart[i] = RowStart[i-1] + RowSize[i-1];
O(columns)
O(terms)
O(columns-1)
row size +1
start size

33. Fast Matrix Transposing (cont’d)
for (i =0; i < Terms; i++) // move from a to b
{
int j = RowStart[smArray[i].col];
b.smArray[j].row = smArray[i].col;
b.smArray[j].col = smArray[i].row;
b.smArray[j].value = smArray[i].value;
RowStart[smArray[i].col]++;
} // end of for
} // end of if
delete [] RowSize;
delete [] RowStart;
return b;
} // end of FastTranspose
O(terms)
O(row * column)
Text
row
row start
row start

34. Matrix Multiplication
Definition: Given A and B, where A is mxn and B
is nxp, the product matrix Result has dimension
mxp. Its [i][j] element is
for 0 ≤ i < m and 0 ≤ j < p.
kj
n
k
ikij baresult ∑
−
=
=
1
0

35. Representation of Arrays
Multidimensional arrays are usually
implemented by one dimensional array via
either row major order or column major
order.
Example: One dimensional array
A[0] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] A[9] A[10] A[11]
α α+1 α+2 α+3 α+4 α+5 α+6 α+7 α+8 α+9 α+10 α+12

36. Two Dimensional Array Row Major
Order
X X X X
X X X X
X X X X
Col 0 Col 1 Col 2 Col u2 - 1
Row 0
Row 1
Row u1 - 1
u2
elements
u2
elements
Row 0 Row 1 Row u1 - 1Row i
i * u2 element
row

37. Generalizing Array Representation
The address indexing of Array A[i1][i2],…,[in] is
α+ i1 u2 u3 … un
+ i2 u3 u4 … un
+ i3 u4 u5 … un
:
:
+ in-1 un
+ in
=α+
=
≤≤= ∏∑ +=
=
1
1
1
1
n
n
jk
kj
n
j
jj
a
njua
whereai

38. String
Usually string is represented as a
character array.
General string operations include
comparison, string concatenation, copy,
insertion, string matching, printing, etc.
H e l l o W o r l d 0

39. String Matching: Straightforward
solution
Algorithm: Simple string matching
Input: P and T, the pattern and text strings; m, the
length of P. The pattern is assumed to be nonempty.
Output: The return value is the index in T where a
copy of P begins, or -1 if no match for P is found.
•Worst-case complexity is in θ(mn)
p: pattern query string
p shift

40. Two Phases of KMP
Phase 1：generate an array to indicate the
moving direction.
Phase 2：make use of the array to move and
match string
phase 1 array
//
shift
shift
phase 2 做matching

41. The first Case for the KMP Algorithm

42. The Second Case for the KMP Algorithm
A shift A

43. The Third Case for the KMP Algorithm
AG
shift AG

44. The KMP Alogrithm
a
a
pattern

45. String Matching The Knuth-Morris-Pratt
Algorithm
Definition: If p = p0p1…pn-1 is a pattern, then its
failure function, f, is defined as
−
≥=<
= +−−
.otherwise1
exists0asuchif......thatsuchlargest
)( 110
kppppppjk
jf jkjkjk
Failure Function
k
P
j
k
k
P
j

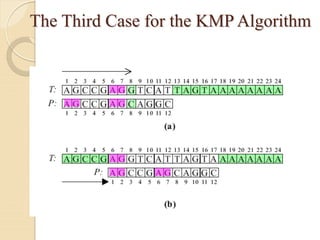
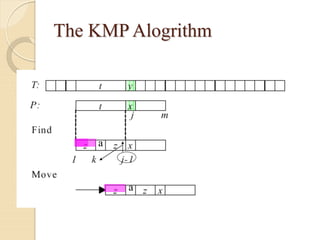
46. The prefix (failure) function, Π
Following pseudocode computes the prefix (i.e., failure) fucnction, Π:
Compute-Prefix-Function (p)
1 m length[p] //’p’ pattern to be matched
2 Π[1] 0
3 k 0
4 for q 2 to m
5 do while k > 0 and p[k+1] != p[q]
6 do k Π[k]
7 If p[k+1] = p[q]
8 then k k +1
9 Π[q] k
10 return Π

47. Example: compute Π for the pattern ‘p’ below:
p a b a b a c a
Initially: m = length[p] = 7
Π[1] = 0
k = 0
Step 1: q = 2, k=0
Π[2] = 0
Step 2: q = 3, k = 0,
Π[3] = 1
Step 3: q = 4, k = 1
Π[4] = 2
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1
q 1 2 3 4 5 6 7
p a b a b a c A
Π 0 0 1 2

48. Step 4: q = 5, k =2
Π[5] = 3
Step 5: q = 6, k = 3
Π[6] = 1
Step 6: q = 7, k = 1
Π[7] = 1
After iterating 6 times, the prefix
function computation is
complete:
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1 2 3
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1 2 3 0
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1 2 3 0 1
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1 2 3 0 1
a =

49. The KMP Alogrithm (cont’d)
jj-1
S
P
Action
k
i
If a partial match is found such that si-j … si-1 =
p0p1…pj-1 and si ≠ pj then matching may be resumed by
comparing si and pf(j–1)+1 if j ≠ 0. If j = 0, we may
continue by comparing si+1 and p0.
fail function pattern array
element = element
f(j-1) +1
f(j-1)
f(j-1) + 1

50. The KMP Matcher
The KMP Matcher, with pattern ‘p’, string ‘S’ and prefix function ‘Π’ as input, finds a match of p in S.
Following pseudocode computes the matching component of KMP algorithm:
KMP-Matcher(S,p)
1 n length[S]
2 m length[p]
3 Π Compute-Prefix-Function(p)
4 q 0 //number of characters matched
5 for i 1 to n //scan S from left to right
6 do while q > 0 and p[q+1] != S[i]
7 do q Π[q] //next character does not match
8 if p[q+1] = S[i]
9 then q q + 1 //next character matches
10 if q = m //is all of p matched?
11 then print “Pattern occurs with shift” i – m
12 q Π[ q] // look for the next match
Note: KMP finds every occurrence of a ‘p’ in ‘S’. That is why KMP does not terminate in step 12,
rather it searches remainder of ‘S’ for any more occurrences of ‘p’.

51. Illustration: given a String ‘S’ and pattern ‘p’ as
follows:
S b a c b a b a b a b a c a c a
p a b a b a c a
Let us execute the KMP algorithm to find
whether ‘p’ occurs in ‘S’.
For ‘p’ the prefix function, Π was computed previously and is as follows:
q 1 2 3 4 5 6 7
p a b a b a c a
Π 0 0 1 2 3 0 1
phase 1 pattern fail function value

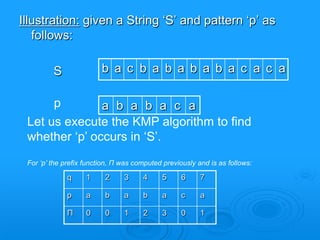
52. b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
a b a b a c a
Initially: n = size of S = 15;
m = size of p = 7
Step 1: i = 1, q = 0
comparing p[1] with S[1]
S
p
P[1] does not match with S[1]. ‘p’ will be shifted one position to the right.
S
p a b a b a c a
Step 2: i = 2, q = 0
comparing p[1] with S[2]
P[1] matches S[2]. Since there is a match, p is not shifted.

53. Step 3: i = 3, q = 1
b a c b a b a b a b a c a a b
Comparing p[2] with S[3]
S
a b a b a c a
b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
a b a b a c a
a b a b a c ap
S
p
S
p
p[2] does not match with S[3]
Backtracking on p, comparing p[1] and S[3] (q= Π[1]+1=0+1=1)
Step 4: i = 4, q = 0
comparing p[1] with S[4] p[1] does not match with S[4]
Step 5: i = 5, q = 0
comparing p[1] with S[5] p[1] matches with S[5]

54. b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
a b a b a c a
a b a b a c a
a b a b a c a
Step 6: i = 6, q = 1
S
p
Comparing p[2] with S[6] p[2] matches with S[6]
S
p
Step 7: i = 7, q = 2
Comparing p[3] with S[7] p[3] matches with S[7]
Step 8: i = 8, q = 3
Comparing p[4] with S[8] p[4] matches with S[8]
S
p

55. Step 9: i = 9, q = 4
Comparing p[5] with S[9]
Comparing p[6] with S[10]
Comparing p[5] with S[11]
Step 10: i = 10, q = 5
Step 11: i = 11, q = 4
S
S
S
p
p
p
b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
a b a b a c a
a b a b a c a
a b a b a c a
p[6] doesn’t match with S[10]
Backtracking on p, comparing p[4] with S[10] because after mismatch q = (Π[5]+1) = 3+1=4
p[5] matches with S[9]
p[5] matches with S[11]
看a fail function = 3
從3+1 開始比

56. b a c b a b a b a b a c a a b
b a c b a b a b a b a c a a b
a b a b a c a
a b a b a c a
Step 12: i = 12, q = 5
Comparing p[6] with S[12]
Comparing p[7] with S[13]
S
S
p
p
Step 13: i = 13, q = 6
p[6] matches with S[12]
p[7] matches with S[13]
Pattern ‘p’ has been found to completely occur in string ‘S’.

57. The analysis of the K.M.P. Algorithm
O(m+n)
– O(m) for computing function f
– O(n) for searching P