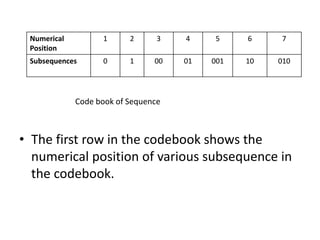
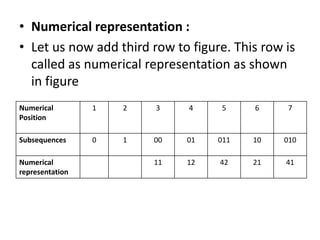
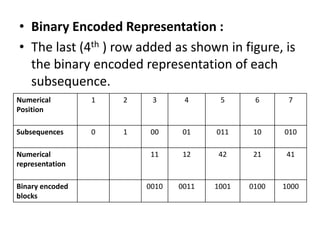
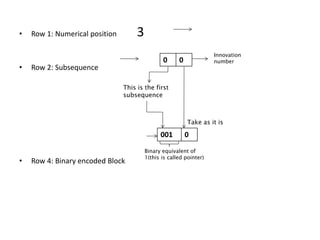
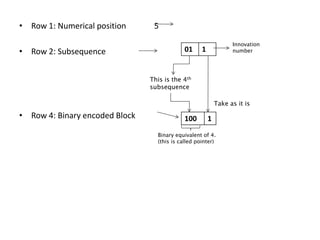
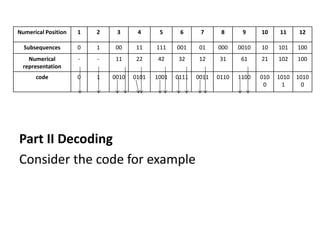
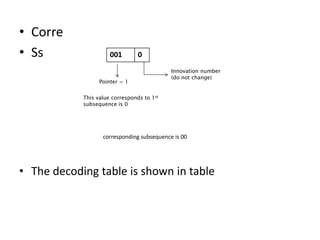
The document provides an introduction to Lempel-Ziv (LZ) algorithms, specifically LZ77 and LZ78, which are lossless data compression techniques. It explains the principles of these algorithms, detailing how they encode and decode data by utilizing previously seen sequences to create a codebook of subsequences. The document also compares the efficiency of LZ algorithms to Huffman coding, illustrating the advantages of LZ in terms of adaptability and implementation simplicity.

1. Introduction to Data communication
Topic : LZ Algorithms
Lecture #14
Dr Rajiv Srivastava
Director
Sagar Institute of Research & Technology (SIRT)
Sagar Group of Institutions, Bhopal
http://www.sirtbhopal.ac.in

2. Unit 1
Lecture 14
2

3. Lampel ZIV (LZ) code
 The Lempel-Ziv algorithm is a variable-to-fixed length
code
 Basically, there are two versions of the algorithm
 LZ77 and LZ78 are the two lossless data compression
algorithms published by Abraham Lempel and Jacob Ziv
in 1977 & 1978. They are also known as LZ1 and LZ2
respectively.
 These two algorithms form the basis for many variations
including LZW, LZSS, LZMA and others. Besides their
academic influence, these algorithms formed the basis of
several ubiquitous compression schemes, including GIF
and the DEFLATE algorithm used in PNG.

4.  They are both theoretically dictionary coders.
 LZ77 keeps track of last n-bytes seen of data & when a
phrase is encountered that already has been seen, it outputs
a pair of values corresponding to the position of pharase in
previously seen buffer data & it moves a fixed size window
over data. It does so by maintaining a sliding window
during compression. This was later shown to be equivalent
to the explicit dictionary constructed by LZ78—however,
they are only equivalent when the entire data is intended to
be decompressed.
 LZ78 decompression allows random access to the input as
long as the entire dictionary is available, while LZ77
decompression must always start at the beginning of the
input.

5.  If we compare it Huffman code then we find the major
disadvantage of the Huffman code is that the symbol
probabilities must be known or estimated if they are
unknown.
 In addition to this, the encoder and Decoder must know
the coding tree.
 Moreover in the modeling text, the storage requirement
prevent the Huffman code from capturing the higher
order relationship between words and phrases.

6. • So we have to compromise the efficiency of
code.
• These practical limitation of Huffman code
can be overcome by using the lampel ZIV
algorithm.
• It is adaptive and simpler to implement as
compared to Huffman coding.

7. • Principal of Lampel ZIV algorithm
• To illustrate this principle let us consider the
example of an input binary sequence specified
as :
000101110010
The encoding in this algorithm is accomplished by parsing
the source data stream into segments that are the shortest
substances not encountered previously.

8. • We assume that the binary symbols 0 and 1 are
already stored in this order in the code book.
Hence we write,
subsequences stored : 0, 1
Data to be parsed : 000101110010
• Now examine the data in above equation from
LHS and find the shortest subsequence which is
not encountered previously. It is 00. so we
include 00 as the next entry in the subsequence
and move00 from data to subsequence as follow :

9. Subsequences stored : 0, 1, 00
Data to be parsed : 010110010
• The next shortest Subsequences which is not
previously repeated is 01. In above equation
Note that we are examining from LHS. Hence
we write,
Subsequences stored : 0, 1, 00, 01
Data to be parsed : 01110010

10. • The next shortest Subsequences which is
previously not encountered is 011. so we
write,
Subsequences stored : 0, 1, 00, 01,011
Data to be parsed : 10010
• Similarly we can continue until the data
stream has been completely parsed. The code
book of binary Subsequences gets ready as
shown in figure

11. Code book of Sequence
• The first row in the codebook shows the
numerical position of various subsequence in
the codebook.
Numerical
Position
1 2 3 4 5 6 7
Subsequences 0 1 00 01 001 10 010

12. • Numerical representation :
• Let us now add third row to figure. This row is
called as numerical representation as shown
in figure
Numerical
Position
1 2 3 4 5 6 7
Subsequences 0 1 00 01 011 10 010
Numerical
representation
11 12 42 21 41

13. The sequences 0 and 1 are originally stored. So
consider the third Subsequences i.e. 00. this is the
first Subsequences in the data stream and it is
made up of concatenation of the first
Subsequences i.e. 0 with itself.
Hence it is represented by 11 in the row of
numerical representation in above figure
Similarly, subsequences 01 obtained by
concatenation of first and second subsequences so
we enter 12 below that.
The remaining subsequences are treated
accordingly.

14. • Binary Encoded Representation :
• The last (4th ) row added as shown in figure, is
the binary encoded representation of each
subsequence.
Numerical
Position
1 2 3 4 5 6 7
Subsequences 0 1 00 01 011 10 010
Numerical
representation
11 12 42 21 41
Binary encoded
blocks
0010 0011 1001 0100 1000

15. • The question is how to obtain binary encoded
blocks.
• the last symbol of each subsequence in the
second row of above figure (called as
codebook) is called as an innovation symbol.
• So the last bit in each binary encoded block
(4th row) is the innovation symbol of the
corresponding subsequence,

16. The remaining bits provide the equivalent
i a y ep ese tatio of the poi te to the
oot su se ue e that at hes the o e i
question except for the innovation symbol.
This can be explained as follow.
1. Consider Numerical position 3 in figure. The
binary encoded block is 0010.
2. Consider Numerical position 5 in figure. It is
partially reproduced below.

17. • Row 1: Numerical position 3
• Row 2: Subsequence
• Row 4: Binary encoded Block
0 0
Innovation
number
001 0
This is the first
subsequence
Take as it is
Binary equivalent of
1(this is called pointer)

18. • Row 1: Numerical position 5
• Row 2: Subsequence
• Row 4: Binary encoded Block
01 1
Innovation
number
This is the 4th
subsequence
100 1
Binary equivalent of 4.
(this is called pointer)
Take as it is

19.  Consider the numerical position 6 in figure.
It is partially reproduced below.
 Row 1: Numerical position 6
 Row 2: Subsequence
 Row 4: Binary encoded Block
 Similarly the other entries in the fourth row are made.
1 0
Innovation
number
This is the 2nd
subsequence
010 0
Take as it is
Binary equivalent of 2.
(this is called pointer)

20. • Decoder
• The decoding is as simple encoding. The steps
followed at the time of decoding are as follows :
• Step 1 : Take the binary encoded block.
For example consider the binary encoded block in
position 5 i.e. 1001
• Step 2 : use the pointer to identify the root
subsequence :

21. • Binary encoded block
• Append the innovation symbol to the subsequence in
step 2:
Append the innovation number i.e. 1 to the root
subsequence of 01 to get the subsequence 011
corresponding to position 5.
100 1
Innovation
numberPointer = 4
Pointer value 4 corresponds
to 4th subsequence i.e. 01

22. Example: Determine the Lempel ZIV code for the following bit
steram
01001111100101000001010101100110000
Recover the original sequence from the encoded stream
• Soln.
• Part 1 : Encoding
• We assume that the binary symbols 0 and1 are
already stored in the code book.
Subsequences stored : 0, 1

23. • Encoding is accomplished by parsing the
source data stream into segment that are
shortest substances, not encountered
previously.
• The given stream of bits can be parsed into
subsequence as shown below :
0, 1, 00, 11, 111, 001, 01, 000, 0010, 10, 101,
100, 110, 000
• The encoding table is as shown in table

24. Part II Decoding
Consider the code for example
Numerical Position 1 2 3 4 5 6 7 8 9 10 11 12
Subsequences 0 1 00 11 111 001 01 000 0010 10 101 100
Numerical
representation
- - 11 22 42 32 12 31 61 21 102 100
code 0 1 0010 0101 1001 0111 0011 0110 1100 010
0
1010
1
1010
0

25. • Corre
• Ss
corresponding subsequence is 00
• The decoding table is shown in table
001 0
Innovation number
(do not change)
Pointer = 1
This value corresponds to 1st
subsequence is 0

26. • Decoding table.
• Thus we get the original sequence back
Code 0010 0101 1001 0111 0011 0110 1100 0100 10101 10100
Innovation bit 0 1 1 1 1 0 0 0 1 0
Pointer 001 010 100 011 001 011 110 010 1010 1010
Decoded
subsequence
0 0 1 1 1 1 1 0 0 1 0 1 0 0 0 0 010 1 0 1 0 1 1 0 0

27. Thank You
Dr Rajiv Srivastava
Director
Sagar Institute of Research & Technology (SIRT)
Sagar Group of Institutions, Bhopal
http://www.sirtbhopal.ac.in