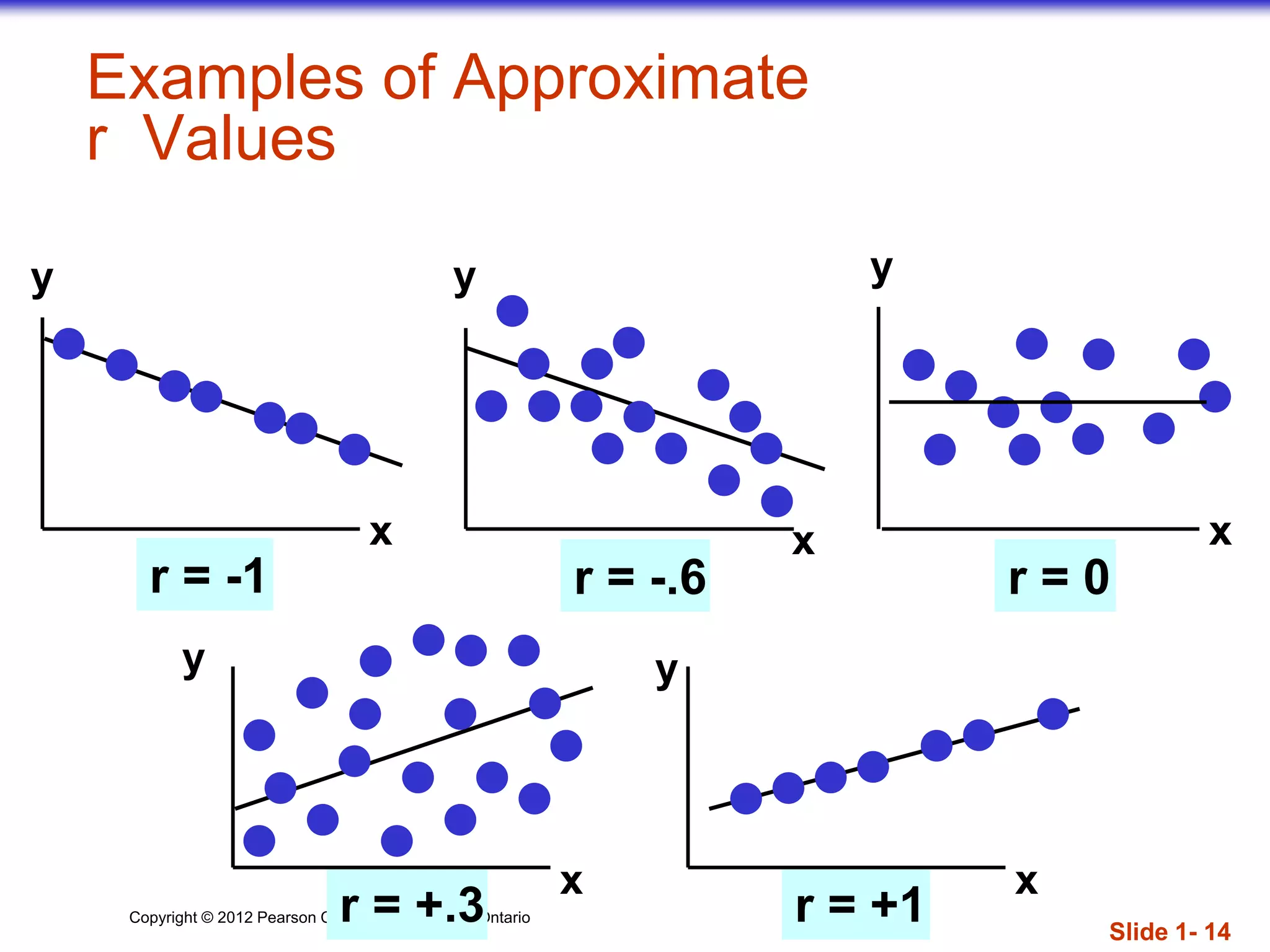
The document discusses correlation and the conditions that must be checked before calculating correlation between two quantitative variables. It explains that correlation measures the strength of the linear association between variables and can only be applied to quantitative, not categorical, variables. Additionally, the relationship must be sufficiently linear for correlation to be valid and outliers can distort results. The document also defines positive and negative correlation and different types of correlation based on the number of variables.

1. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Conditions
 Correlation measures the strength of the linear
association between two quantitative variables.
 Before you use correlation, you must check
several conditions:
 Quantitative Variables Condition
 Straight Enough Condition
 Outlier Condition
Slide 1- 1

2. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Conditions (cont.)
 Quantitative Variables Condition:
 Correlation applies only to quantitative
variables.
 Don’t apply correlation to categorical data
masquerading as quantitative.
 Check that you know the variables’ units and
what they measure.
Slide 1- 2

3. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Conditions (cont.)
 Straight Enough Condition:
 You can calculate a correlation coefficient for
any pair of variables.
 But correlation measures the strength only of
the linear association, and will be misleading if
the relationship is not linear.
Slide 1- 3

4. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Conditions (cont.)
 Outlier Condition:
 Outliers can distort the correlation dramatically.
 An outlier can make an otherwise small
correlation look big or hide a large correlation.
 It can even give an otherwise positive
association a negative correlation coefficient
(and vice versa).
 When you see an outlier, it’s often a good idea
to report the correlations with and without the
point.
Slide 1- 4

5. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Types of correlation
On the basis of
degree of
correlation
On the basis of
number of variables
On the basis of
linearity
•Positive
correlation
•Negative
correlation
•Simple
correlation
•Partial correlation
•Multiple
correlation
•Linear
correlation
•Non – linear
correlation
Slide 1- 5

6. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation : On the basis of degree
 Positive Correlation
if one variable is increasing and with its
impact on average other variable is also
increasing that will be positive correlation.
For example :
Income ( Rs.) : 350 360 370 380
Weight ( Kg.) : 30 40 50 60
Slide 1- 6

7. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation : On the basis of degree
 Negative correlation
if one variable is increasing and with its
impact on average other variable is also
decreasing that will be positive
correlation.
For example :
Income ( Rs.) : 350 360 370 380
Weight ( Kg.) : 80 70 60 50
Slide 1- 7

8. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation : On the basis of number of
variables
 Simple correlation
Correlation is said to be simple when only two
variables are analyzed.
For example :
Correlation is said to be simple when it is done
between demand and supply or we can say
income and expenditure etc.
Slide 1- 8

9. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation : On the basis of number of
variables
 Partial correlation :
When three or more variables are considered for
analysis but only two influencing variables are
studied and rest influencing variables are kept
constant.
For example :
Correlation analysis is done with demand, supply
and income. Where income is kept constant.
Slide 1- 9

10. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation : On the basis of number of
variables
 Multiple correlation :
In case of multiple correlation three or more
variables are studied simultaneously.
For example :
Rainfall, production of rice and price of rice are
studied simultaneously will be known are
multiple correlation.
Slide 1- 10

11. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Properties
 Correlation treats x and y symmetrically:
 The correlation of x with y is the same as the
correlation of y with x.
 Correlation has no units.
 Correlation is not affected by changes in the
centre or scale of either variable.
 Correlation depends only on the z-scores, and
they are unaffected by changes in centre or
scale.
Slide 1- 11

12. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Correlation Properties
 Correlation measures the strength of the linear
association between the two variables.
 Variables can have a strong association but
still have a small correlation if the association
isn’t linear.
 Correlation is sensitive to outliers. A single
outlying value can make a small correlation large
or make a large one small.
Slide 1- 12

13. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Features of the correlation coefficient r
 Unit free
 Range between -1 and 1
 The closer to -1, the stronger the negative linear
relationship
 The closer to 1, the stronger the positive linear
relationship
 The closer to 0, the weaker the linear
relationship
Slide 1- 13

14. Copyright © 2012 Pearson Canada Inc., Toronto, Ontarior = +.3 r = +1
Examples of Approximate
r Values
y
x
y
x
y
x
y
x
y
x
r = -1 r = -.6 r = 0
Slide 1- 14

15. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Calculating the
Correlation Coefficient





])yy(][)xx([
)yy)(xx(
r
22
where:
r = Sample correlation coefficient
n = Sample size
x = Value of the independent variable
y = Value of the dependent variable
   




])y()y(n][)x()x(n[
yxxyn
r
2222
Sample correlation coefficient:
or the algebraic equivalent:
Slide 1- 15

16. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
Calculation Example
Tree
Height
Trunk
Diameter
y x xy y2 x2
35 8 280 1225 64
49 9 441 2401 81
27 7 189 729 49
33 6 198 1089 36
60 13 780 3600 169
21 7 147 441 49
45 11 495 2025 121
51 12 612 2601 144
=321 =73 =3142 =14111 =713
Slide 1- 16

17. Copyright © 2012 Pearson Canada Inc., Toronto, Ontario
0
10
20
30
40
50
60
70
0 2 4 6 8 10 12 14
0.886
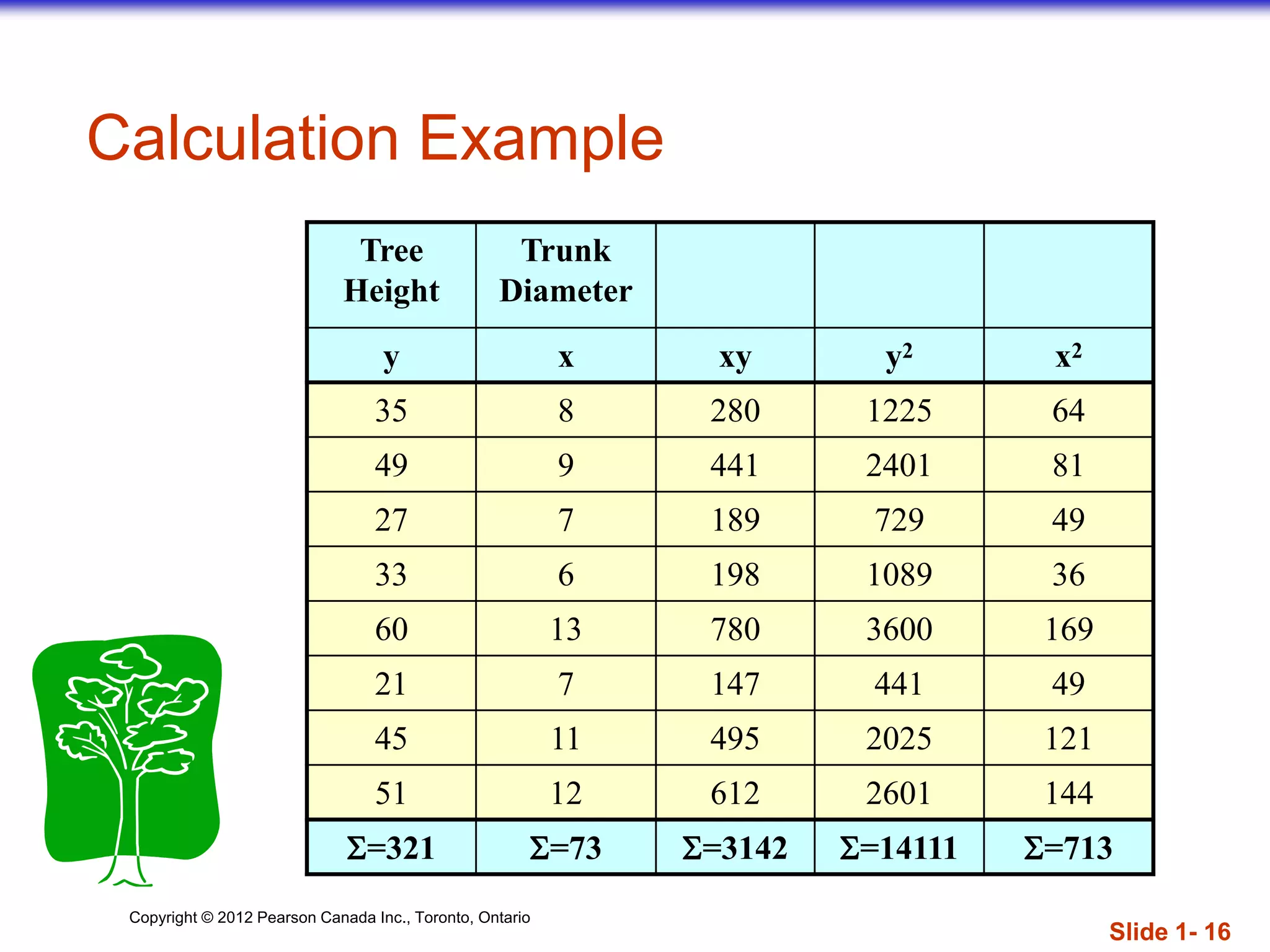
](321)][8(14111)(73)[8(713)
(73)(321)8(3142)
]y)()y][n(x)()x[n(
yxxyn
r
22
2222







   
  
Trunk Diameter, x
Tree
Height,
y
Calculation Example
(continued)
r = 0.886 → relatively strong positive
linear association between x and y
Slide 1- 17