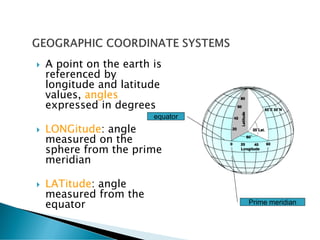
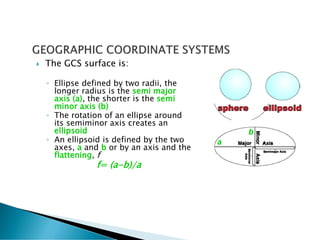
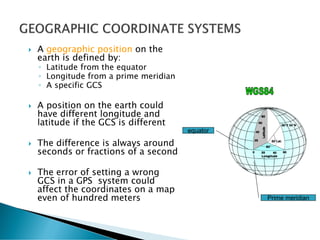
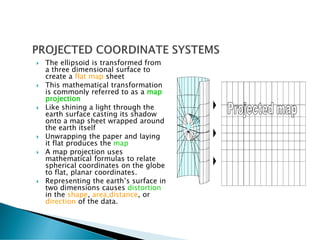
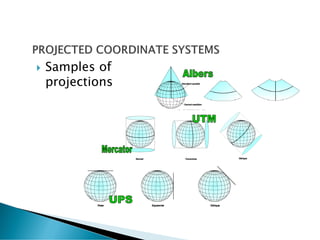
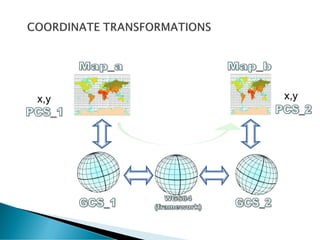
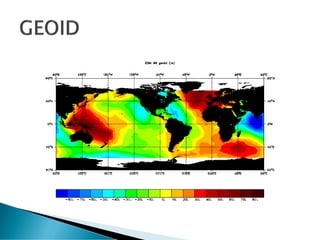
The document discusses coordinate systems and geo-referencing. It describes geographic coordinate systems (GCS) which use latitude and longitude based on an ellipsoid and datum. It also describes projected coordinate systems (PCS) which use x,y coordinates on a flat plane for mapping purposes. The document outlines how different map projections transform the ellipsoid to the flat plane, introducing various types of distortion. It emphasizes the importance of coordinate systems and transformations for accurately locating points on maps and overlaying spatial data.