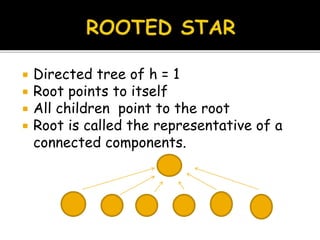
The document discusses connected components labeling algorithms for graphs. It evaluates parallel algorithms on CPU and GPU architectures for different types of graphs. The key algorithms discussed are disjoint set union and depth first search. It proposes a simple auto-tuned approach to select the best technique for a given graph and evaluates the algorithms on real and synthetic datasets ranging from 1-7 million nodes.

1. CONNECTED COMPOUNDS

2.  Studied implemented and evaluated
various parallel algorithms for
connected components labeling in
graphs.
 Two Architectures
 CPU– (OpenMp) and (CUDA)
 Different types of graphs.
 Propose simple auto tuned approach for
choosing best technique for a graph.

3.  Motivation
 Definitions
 Basic Algorithm
 Optimizations
 Datasets and Experiments
 Auto tuning
 Future Scope

4.  Identify vertices that form a
connected set in a graph.
 Used in:
 Pattern Recognition
 Physics
 Biology
 Social Network Analysis

5.  Image Processing
 Pattern Recognition
 Gesture Recognition
Spee
d
Limit
40
Speed
Limit
40
Spee
d
Limit
40

6.  Disjoint Set Union
Make Set
Union
Link
Find Set
 Depth First Search

7.  Directed tree of h = 1
 Root points to itself
 All children point to the root
 Root is called the representative of a
connected components.

8.  ( I,J ) is an edge in the graph.
 If i and j are currently in
differently trees.
 Merge the two trees in to one.
 Make representation of one,
point to the representative of
the other.

9.  Merging two trees T1 and T2.
 Whose representative should be
changed?
 Toss a coin and choose a winner
 Tree with lower index wins always
 Alternate between iterations
(Even, Odd)
 Tree with greater height wins

10.  Move a node higher in the tree.
Single level
Multi level
Final Aim
 EXAMPLE:
 Singletons
 Hooking
 Point jumping

11.  Single instance edge storage
( u,v ) is same as (u,v)
Reduced Memory Footprint
Smaller traversal overhead
 Unconditional Hooking
Calling at appropriate iteration
helps in decreasing the number of
iterations.

12.  Only form stars in every iteration.
 No overhead in determining if a node is
part of a star.

13.  Random graphs
1Mto 7M nodes, average degree 5
 RMAT Graphs
Synthetic Social Networking
1M to 7M nodes
 Real world Data
 Web graphs
Google web
Berkeley Stanford domains

14. Thank you!!!