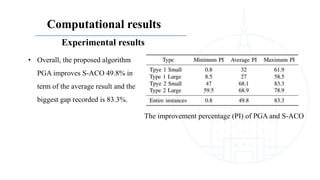
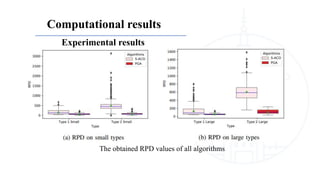
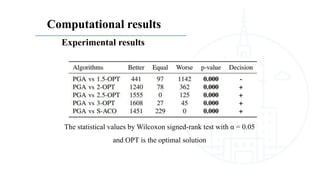
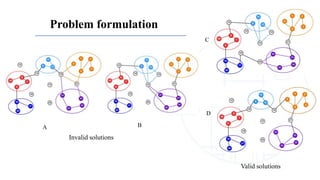
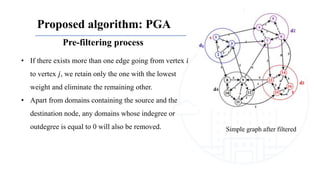
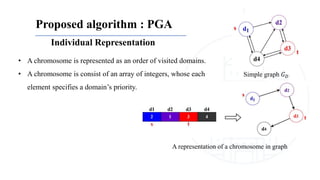
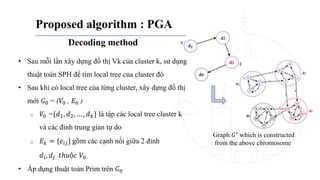
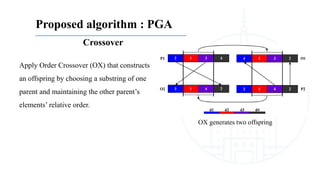
This document describes a genetic algorithm called PGA for solving the clustered Steiner tree problem (CluSteiner). The CluSteiner problem involves finding the minimum cost tree that connects target vertices while satisfying constraints that trees within each cluster are disjoint. PGA uses a two-level approach, first finding local trees for each cluster and then linking the trees. It represents solutions as an ordering of clusters and applies crossover and mutation genetic operators. Computational experiments show PGA improves on previous algorithms by up to 83% on test instances.


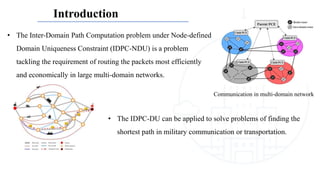
![Related works
• [1] L. Maggi, J. Leguay, J. Cohen, and P. Medagliani, “Domain clustering for inter-domain path
computation speed-up,” Networks, vol. 71, no. 3, pp. 252–270, 2018.
o Introduce two variants of the IDPC-DU and prove their NP-Hard property.
o Propose a dynamic programming approach whose complexity is 𝑂( 𝑉 22|𝐷||𝐷|2) (where 𝑉 is
the number of nodes, and 𝐷 is the number of domains)
• [2] H. T. T. Binh, T. B. Thangy, N. B. Long, N. V. Hoang, and P. D. Thanh, “Multifactorial
evolutionary algorithm for inter-domain path computation under domain uniqueness constraint,” in
2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020, pp. 1–8.
o Adopt Multifactorial evolutionary algorithm (MFEA) to solve the IDPC-EDU.
o Use two-layer encryption based on the Priority-based Encoding.](https://image.slidesharecdn.com/onclusteredsteinertree-slidever1-211228061527/85/On-clusteredsteinertree-slide-ver-1-1-4-320.jpg)




![Computational results
• Instance datasets are generated based on a set of Non-Euclidean CluSPT [1].
• The datasets are categorized into two kinds regarding dimensionality: small
instances, each of which has between 30 and 120 vertices, and large instances, each
of which has over 260 vertices.
Problem instances
[1] Thanh Pham Dinh. “CluSPT Instances,Mendeley Data, V3”. In: (2019). DOI: 10.17632/b4gcgybvt6.3.](https://image.slidesharecdn.com/onclusteredsteinertree-slidever1-211228061527/85/On-clusteredsteinertree-slide-ver-1-1-14-320.jpg)

![Computational results
• The SPH algorithm is compared with an MST algorithm in the previous work [1].
• SGA setups: the random mating probability (pc) is 0.8, the mutation rate (pm) is 0.05.
• All algorithms maintain a population with 100 individuals under 50000 evaluations.
Experimental setup
[10] D. Sudholt and C. Thyssen, “A simple ant colony optimizer for stochastic shortest path problems,” Algorithmica, vol.
64, no. 4, pp. 643–672, 2012](https://image.slidesharecdn.com/onclusteredsteinertree-slidever1-211228061527/85/On-clusteredsteinertree-slide-ver-1-1-16-320.jpg)