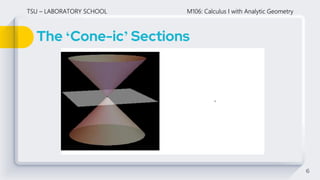
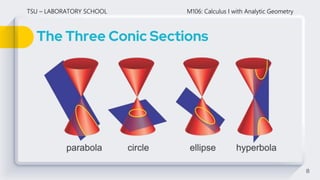
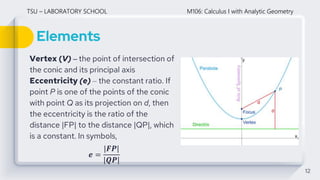
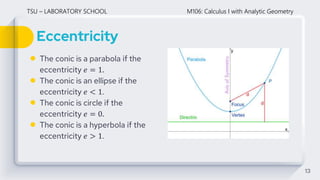
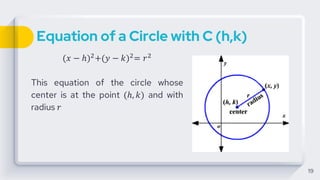
This document discusses conic sections and circles. It defines conic sections as curves formed by the intersection of a plane and a double right circular cone. The main conic sections are parabolas, ellipses, hyperbolas, and circles. Circles are specifically defined as sets of points equidistant from a fixed center point. The document derives the standard and general forms of the equation of a circle, and provides examples of writing equations of circles given properties like center and radius.

1. CONIC
SECTIONS
Jay-Art F. Agustin
TSU – LABORATORY SCHOOL Pre-Calculus for Grade 11 STEM

2. Objectives:
2
● Illustrate the different types of conic sections – parabola,
hyperbola, ellipse, circle, and degenerate cases;
● Define a circle;
● Determine the standard from of equation of a circle; and
● Graph a circle in the rectangular coordinate plane.
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

3. Conic Sections
1
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

4. The Origin
4
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry
Apollonius of Perga
● Greek Geometer
● Studies the curves formed
by the intersection of a
plane and a double right
circular cone.

5. The ‘Cone-ic’ Sections
5
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry
● Conic section is a curve
formed by the
intersection of a plane
and a double right circular
cone.

6. The ‘Cone-ic’ Sections
6
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

7. The Three Conic Sections
7
● Parabola is formed if the cutting plane is parallel to one and
only one generator
● Ellipse is formed if the cutting of the plane is not parallel to
any generator.
○ Circle is formed if the cutting of the plane is not parallel
to any to any generator but is perpendicular to the axis.
● Hyperbola is formed if the cutting plane is parallel to two
generators.
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

8. The Three Conic Sections
8
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

9. Degenerate Conic Sections
9
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

10. Conic Sections as Defined
10
● A conic is a set of points
whose distances from a
fixed point are in constant
ratio to their distances
from a fixed line that is not
passing through the fixed
point.
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

11. Elements
11
Focus (F) – the fixed point of a conic
Directrix (d) – the fixed line d
corresponding to the focus.
Principal axis (a) – a line that
passes through the focus and
perpendicular to the directrix. Every
conic is symmetric with respect to its
principal axis.
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

12. Elements
12
Vertex (V) – the point of intersection of
the conic and its principal axis
Eccentricity (e) – the constant ratio. If
point P is one of the points of the conic
with point Q as its projection on d, then
the eccentricity is the ratio of the
distance |FP| to the distance |QP|, which
is a constant. In symbols,
𝒆 =
|𝑭𝑷|
|𝑸𝑷|
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

13. Eccentricity
13
● The conic is a parabola if the
eccentricity 𝑒 = 1.
● The conic is an ellipse if the
eccentricity 𝑒 < 1.
● The conic is circle if the
eccentricity 𝑒 = 0.
● The conic is a hyperbola if the
eccentricity 𝑒 > 1.
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

14. Circles
2
TSU – LABORATORY SCHOOL M106: Calculus I with Analytic Geometry

15. Circle Defined
A circle is a set of all coplanar
points such that the distance from
a fixed point is constant. The fixed
point is called the center of the
circle and the constant distance
from the center is called the
radius of the circle.
15

16. Circle Defined
A circle is a set of all coplanar points
such that the distance from a fixed
point is constant. The fixed point is
called the center of the circle and
the constant distance from the
center is called the radius of the
circle.
16

17. Equation of a Circle with C (0, 0)
𝑥2
+ 𝑦2
= 𝑟2
This equation is referred to as the
standard form of equation of a circle
whose center is at the origin with
radius r.
This can be derived using the
distance formula.
17

18. Derivation
𝑥2
+ 𝑦2
= 𝑟2
The distance of C (0,0) to P (x, y) is equal to the radius.
18

19. Equation of a Circle with C (h,k)
(𝑥 − ℎ)2
+(𝑦 − 𝑘)2
= 𝑟2
This equation of the circle whose
center is at the point (ℎ, 𝑘) and with
radius 𝑟
19

20. Exercise
Determine the standard form of equation of the following circles
and the radius. Draw the graph.
1. Center 𝐶(0, 0), radius: 9;
2. Center 𝐶(−5,7), radius: 6;
3. Center 𝐶( 7, 3 3), radius: 8.
20

21. Exercise
1. Center 𝐶(0, 0), radius: 9
21

22. Exercise
1. Center 𝐶(−5,7), radius: 6
22

23. Exercise
1. Center 𝐶( 7, 3 3), radius: 8
23

24. Equation of a Circle in GF
𝒙𝟐 + 𝒚𝟐 + 𝑫𝒙 + 𝑬𝒚 + 𝑭 = 𝟎,
where 𝐷 = −2ℎ, E = −2k, and F = ℎ2
+ 𝑘2
− 𝑟2
This general form was derived by expanding the standard form of
the equation.
24

25. Derivation
𝒙𝟐 + 𝒚𝟐 + 𝑫𝒙 + 𝑬𝒚 + 𝑭 = 𝟎,
where 𝐷 = −2ℎ, E = −2k, and F = ℎ2
+ 𝑘2
− 𝑟2
25
(𝑥 − ℎ)2
+(𝑦 − 𝑘)2
= 𝑟2

26. Examples
Write the equation of a circle in general form with center at (−3, −2) and
radius of 4.
26

27. Examples
Write the equation of a circle in general form with center at (−4, 6) and
radius of 5.
27

28. Examples
Write the equation of a circle in general form with center at (2, −4) and
radius of 5.
28

29. Examples
Determine the center and radius of the circle in general form.
𝑥2 + 𝑦2 − 4𝑥 − 2𝑦 − 4 = 0
29

30. Examples
Determine the center and radius of the circle in general form.
𝑥2 + 𝑦2 − 10𝑥 − 6𝑦 − 18 = 0
30

31. Examples
Determine the center and radius of the circle in general form.
2𝑥2 + 2𝑦2 − 16𝑥 + 12𝑦 − 4 = 0
31

32. Equation of a Circle in GF
𝒙𝟐 + 𝒚𝟐 + 𝑫𝒙 + 𝑬𝒚 + 𝑭 = 𝟎,
where 𝐷 = −2ℎ, E = −2k, and F = ℎ2
+ 𝑘2
− 𝑟2
Solving for r in terms of D, E, and F in the general form:
If
𝐷2
4
+
𝐸2
4
− 𝐹 > 0, then the graph of the equation is a circle.
If
𝐷2
4
+
𝐸2
4
− 𝐹 = 0, then the graph of the equation is a point circle.
If
𝐷2
4
+
𝐸2
4
− 𝐹 < 0, the equation has no graph.
32

33. Examples
Determine whether the equation represents a circle, a point circle, or
has no graph.
𝑥2 + 𝑦2 + 8𝑥 + 15 = 0
33

34. Examples
Determine whether the equation represents a circle, a point circle, or
has no graph.
𝑥2 + 𝑦2 + 87𝑥 + 5𝑦 + 16 = 0
34

35. Examples
Determine whether the equation represents a circle, a point circle, or
has no graph.
𝑥2 + 𝑦2 + 2𝑥 − 6𝑦 + 12 = 0
35

36. Examples
Find the general equation of a circle.
The center of the circle is at ( -3, 7) and goes through the origin.
36

37. Examples
Find the general equation of a circle.
The center of the circle is at (7, 4) and goes through the point (4, 8)
37

38. Examples
Find the equation of a circle
The circle passes through the origin, and contain the points (0, 5), and (3, 3).
𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0
38

39. Examples
Find the equation of a circle
The circle passes through the origin, and contain the points (0, 8), and (5, 5).
𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0
39

40. Examples
Find the equation of a circle
The circle passes through the points (2, 3), (6, 1), and (4, -3).
𝑥2
+ 𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0
40

41. Examples
A particular cellphone tower is designed to service a 15-km radius. The tower is located at
(5, -3) on a coordinate plane whose units represents km.
● What is the standard form equation of the outer boundary of the region serviced by
the tower?
● What is the general form equation of the region serviced by the tower?
● Draw the graph of the region serviced by the tower.
41

42. Meronnnn paaaa!
42