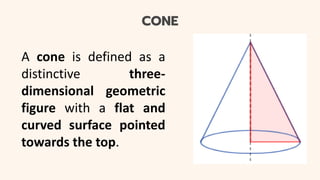
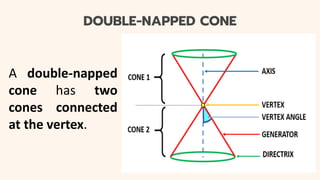
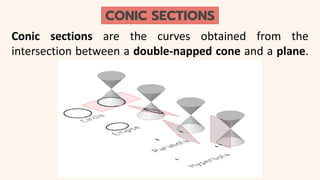
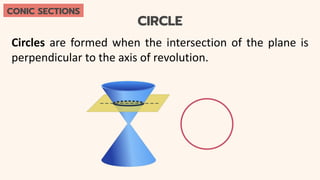
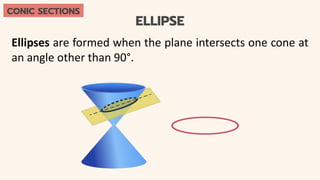
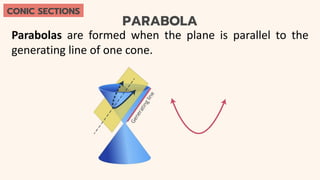
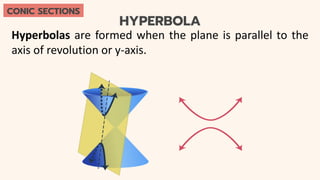
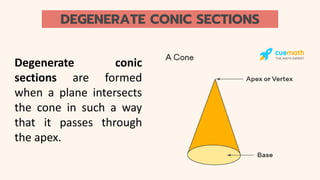
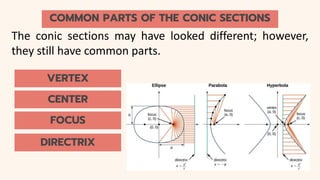
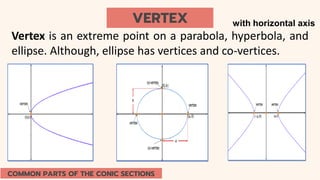
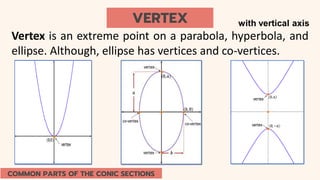
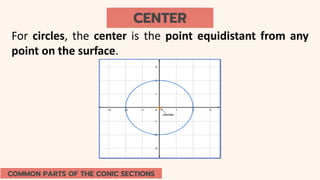
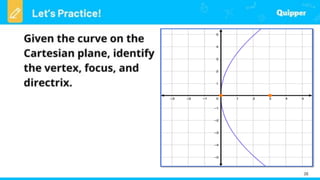
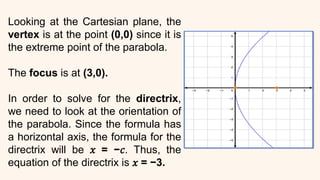
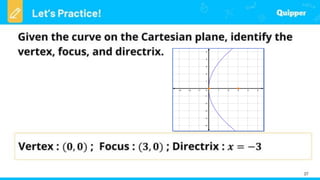
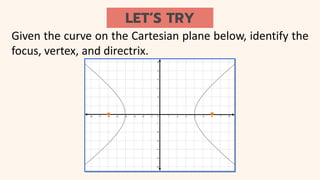
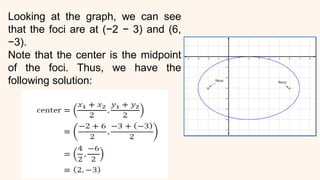
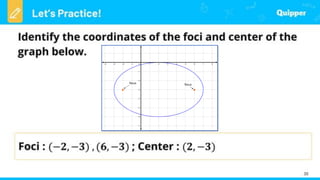
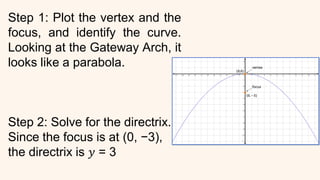
This document provides an introduction to conic sections, including circles, ellipses, parabolas, hyperbolas, and degenerate cases. It defines key terms like cones, double-napped cones, vertices, foci, directrices, and centers. Examples are given of different conic sections formed by varying the intersection of planes with double-napped cones. The common elements of conic sections are discussed and illustrated. Examples are worked through to identify the foci, vertices and directrices of parabolas based on their graphs. An assessment with questions is included to test understanding.

1. INTRODUCTION
TO CONIC
SECTIONS
PRE-CALCULUS
STEM 11

2. LEARNING OBJECTIVES
At the end of this lesson, you are expected to:
• illustrate the different types of conic sections: parabola,
ellipse, circle, hyperbola, and degenerate cases
• define a circle
• determine the standard form of equation of a circle
• define a parabola
• determine the standard form of equation of a parabola

3. TYPES OF
CONIC
SECTIONS
01

4. CONE
A cone is defined as a
distinctive three-
dimensional geometric
figure with a flat and
curved surface pointed
towards the top.

5. DOUBLE-NAPPED CONE
A double-napped
cone has two
cones connected
at the vertex.

6. ACTIVITY: DRAW THAT CURVE

7. CONIC SECTIONS
Conic sections are the curves obtained from the
intersection between a double-napped cone and a plane.

8. CIRCLE
Circles are formed when the intersection of the plane is
perpendicular to the axis of revolution.
CONIC SECTIONS

9. ELLIPSE
Ellipses are formed when the plane intersects one cone at
an angle other than 90°.
CONIC SECTIONS

10. PARABOLA
Parabolas are formed when the plane is parallel to the
generating line of one cone.
CONIC SECTIONS

11. HYPERBOLA
Hyperbolas are formed when the plane is parallel to the
axis of revolution or y-axis.
CONIC SECTIONS

12. DEGENERATE CONIC SECTIONS
Degenerate conic
sections are formed
when a plane intersects
the cone in such a way
that it passes through
the apex.

13. DEGENERATE CONIC SECTIONS
Degenerate conic sections are formed when a plane
intersects the cone in such a way that it passes through
the apex.

14. INTERACTIVE 3D OF CONIC
SECTIONS
https://www.intmath.com/plane-analytic-
geometry/conic-sections-summary-interactive.php

15. COMMON PARTS OF THE CONIC SECTIONS
The conic sections may have looked different; however,
they still have common parts.
VERTEX
CENTER
FOCUS
DIRECTRIX

16. COMMON PARTS OF THE CONIC SECTIONS
VERTEX
Vertex is an extreme point on a parabola, hyperbola, and
ellipse. Although, ellipse has vertices and co-vertices.
with horizontal axis

17. COMMON PARTS OF THE CONIC SECTIONS
VERTEX
Vertex is an extreme point on a parabola, hyperbola, and
ellipse. Although, ellipse has vertices and co-vertices.
with vertical axis

18. COMMON PARTS OF THE CONIC SECTIONS
FOCUS AND DIRECTRIX
The focus and directrix are the point and the line on a conic section
that are used to define and construct the curve respectively. The
distance of any point on the curve from the focus to the directrix is
proportion as shown on the images below by the green lines. In a
plane, the circle has no defined directrix.
with horizontal axis

19. COMMON PARTS OF THE CONIC SECTIONS
FOCUS AND DIRECTRIX
The focus and directrix are the point and the line on a conic section
that are used to define and construct the curve respectively. The
distance of any point on the curve from the focus to the directrix is
proportion as shown on the images below by the green lines. In a
plane, the circle has no defined directrix.
with vertical axis

20. COMMON PARTS OF THE CONIC SECTIONS
CENTER
For circles, the center is the point equidistant from any
point on the surface.

26. Looking at the Cartesian plane, the
vertex is at the point (0,0) since it is
the extreme point of the parabola.
The focus is at (3,0).
In order to solve for the directrix,
we need to look at the orientation of
the parabola. Since the formula has
a horizontal axis, the formula for the
directrix will be 𝑥 = −𝑐. Thus, the
equation of the directrix is 𝑥 = −3.

28. LET’S TRY
Given the curve on the Cartesian plane below, identify the
focus, vertex, and directrix.

30. Looking at the graph, we can see
that the foci are at (−2 − 3) and (6,
−3).
Note that the center is the midpoint
of the foci. Thus, we have the
following solution:

32. LET’S TRY
Identify the coordinates of the foci and the center of the
graph below.

34. Step 1: Plot the vertex and the
focus, and identify the curve.
Looking at the Gateway Arch, it
looks like a parabola.
Step 2: Solve for the directrix.
Since the focus is at (0, −3),
the directrix is 𝑦 = 3

43. ASSESSMENT

44. A. Identify the conic section or the part that is being
described.
1. These are the conic sections that are formed when the
plane intersects the double-napped cone in such a way that
it passes through the apex.
2. This conic section is formed when the plane is parallel to
the axis of revolution.
3. It is the midpoint of the two foci for ellipse and hyperbola.
4. It refers to the extreme point of a parabola.
5. These are the curves that are obtained between the
intersection of a double-napped cone and a plane.
ASSESSMENT

45. B.Using the image below, complete the table and
solve for the directrix given the vertices and foci.

48. Assignment: Challenge Yourself
Answer the following questions:
1. You saw Albert playing with a double-napped cone and a paper. He
put the paper on top of one cone and said that he was able to form a
conic section. Do you agree with him? Explain your answer.
2. A glass was placed on the table. If you hold a flashlight as shown
below, what kind of curve will be formed by its shadow?
3. If you shift a parabola with vertex at the origin, two units to the right,
what will be the new vertex?