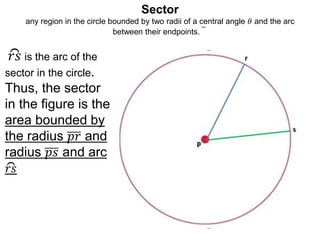
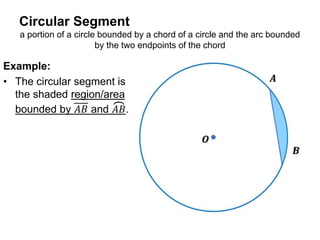
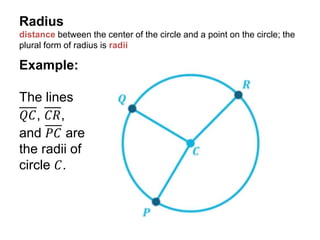
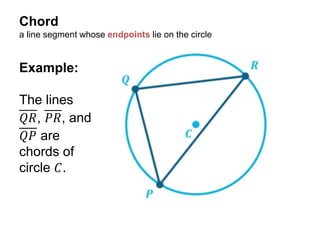
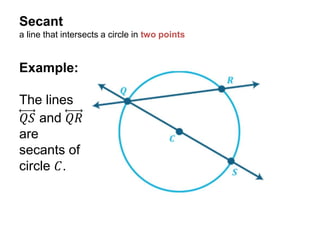
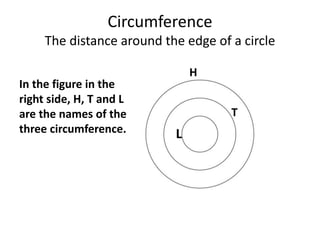
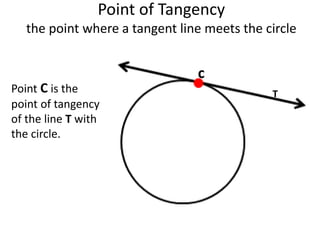
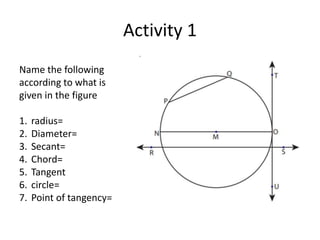
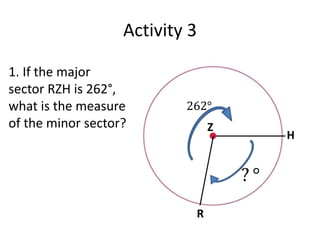
This document defines and provides examples of key terms used in geometry to describe parts of a circle, including radius, diameter, chord, secant, tangent, sector, arc, circular segment, circumference, point of tangency, and circle. It also includes example problems asking the reader to name these parts based on diagrams and calculate values like the measure of an angle or area of a segment.

1. Naming parts of a Circle
Naming parts of a circle is practically
and technically important in such a
way that it systematically allows us
to compute areas, linear measure of
arcs and circumference, and lengths
of segments in a circle.

3. Sector
any region in the circle bounded by two radii of a central angle 𝜃 and the arc
between their endpoints.
𝑟𝑠 is the arc of the
sector in the circle.
Thus, the sector
in the figure is the
area bounded by
the radius 𝑝𝑟 and
radius 𝑝𝑠 and arc
𝑟𝑠

4. Arc
a portion of the circle’s circumference.
Example:
• The curve line
connecting
points A and B
is an example
of an arc. This
is 𝐴𝐵.

5. Circular Segment
a portion of a circle bounded by a chord of a circle and the arc bounded
by the two endpoints of the chord
Example:
• The circular segment is
the shaded region/area
bounded by 𝐴𝐵 and 𝐴𝐵.

6. Radius
distance between the center of the circle and a point on the circle; the
plural form of radius is radii
Example:
The lines
𝑄𝐶, 𝐶𝑅,
and 𝑃𝐶 are
the radii of
circle 𝐶.

7. Chord
a line segment whose endpoints lie on the circle
Example:
The lines
𝑄𝑅, 𝑃𝑅, and
𝑄𝑃 are
chords of
circle 𝐶.

8. Diameter
a chord that passes through the center of the circle; the diameter is also the
longest chord in a circle
Example:
The line
𝑄𝑆 is the
diameter
of circle 𝐶.

9. Secant
a line that intersects a circle in two points
Example:
The lines
𝑄𝑆 and 𝑄𝑅
are
secants of
circle 𝐶.

10. Tangent
a line that intersects a circle at only one point; the point where it
intersects the circle is called the point of tangency
Example:
The line 𝑈𝑉
is tangent to
circle 𝐶, and
the point of
tangency is
point 𝑇.

11. Circumference
The distance around the edge of a circle
H
T
L
In the figure in the
right side, H, T and L
are the names of the
three circumference.

12. Point of Tangency
the point where a tangent line meets the circle
c
Point C is the
point of tangency
of the line T with
the circle.
T

13. Circle
a set of all points equidistant from a fixed point called
the center of the circle
P
P is the name
of the circle

14. How many degrees is there in the
Circle?
There is a total of
360°within a circle.
Therefore, if in figure
, the minor sector CAB
is 145°, the remaining
major sector is 360° -
145° = 215°
A
C
B
145°
?

15. Activity 1
Name the following
according to what is
given in the figure
1. radius=
2. Diameter=
3. Secant=
4. Chord=
5. Tangent
6. circle=
7. Point of tangency=

16. Acitvity 2
Name the following
according to what is
given in the figure
1. Circle=
2. Centre=
3. Circular segment=
4. Line segment=
5. Circumference =
6. Sector=
7. Arc=
K

17. Activity 3
Z
R
H
262°
? °
1. If the major
sector RZH is 262°,
what is the measure
of the minor sector?

18. 2. If the total area
of the circle is 350
sq. cm and the
major Circular
Segment AB is
330, what is the
area of the minor
Circular Segment
AB?
Activity 3