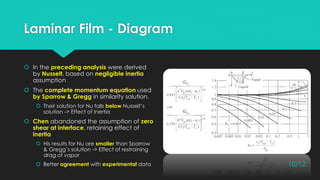
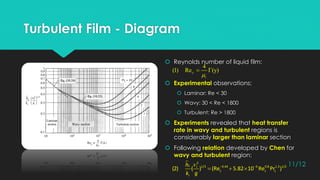
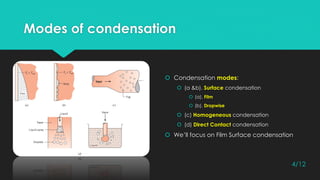
This document discusses condensation and film surface condensation on vertical surfaces. It defines condensation as the phase change from gas to liquid, and describes different types including surface, homogeneous, and direct contact condensation. For film surface condensation, it notes there are three regions - laminar, wavy, and turbulent - depending on the Reynolds number of the liquid film. It reviews the derivation of the laminar film condensation equation first solved by Nusselt, and improvements made by Sparrow and Gregg and Chen to account for inertia effects and vapor drag. Finally, it presents Chen's developed relation for calculating the heat transfer coefficient in the wavy and turbulent film regions.

1. Condensation on
vertical surface
Convective Heat Transfer Seminar
Mostafa Ghadamyari
M. SC. Student
Spring 2014 - Tarbiat Modares university

2. Outline
 Here, We will discuss about:
 Condensation definition
 Different types of condensation
 Film Surface Condensation
 Laminar film equation derivation
 Laminar film heat transfer coefficient diagram
 Turbulent Film heat transfer coefficient diagram
2/12

3. Condensation definition
 A phase is a region of space (a
thermodynamic system), throughout
which all physical properties of a material
are essentially uniform.
 A phase transition is the transformation of
a thermodynamic system from one phase
or state of matter to another one by heat
transfer.
 Condensation is the change of the
physical state of matter from gas phase
into liquid phase, and is the reverse of
vaporization
3/12

4. Modes of condensation
 Condensation modes:
 (a &b). Surface condensation
 (a). Film
 (b). Dropwise
 (c) Homogeneous condensation
 (d) Direct Contact condensation
 We’ll focus on Film Surface condensation
4/12

5. Dropwise and Film Surface condensation
 (a) Dropwise condensation occurs if the
surface is coated with a substance that
inhibits wetting, Silicones, Teflon,
assortment of waxes and fatty acids
 (b) Film condensation is generally
characteristic of clean, uncontaminated
surfaces
 The condensate provides a resistance to
heat transfer between the vapor and the
surface
 It’s desirable but difficult to maintain
dropwise condensation, so calculations
are often based on Film condensation
5/12

6. Film condensation
 Film condensation has Three distinct regions:
 1. Laminar region, near the top, the film is
relatively thin
 2. Wavy region, The film becomes thick enough
to show the signs of transition
 3. Turbulent region, Ripples appear irregular in
both space and time
 Laminar Region complexities:
 Flow of liquid interacts with layer of vapor
 Tinterface= Saturation temperature of local P
 Tw < Saturation temperature < Tvapor
6/12

7. Laminar Film – Momentum Equation
 Momentum equation for simplified laminar film:
 Because of slenderness of the film:
 Substituting:
 Assuming negligible Inertia [Solved by Nusselt]:
  
   
        
2
2
(1) l l l
v v dP v
u v g
x y dy x
   

   
       
2
2
(3) ( )l l l v
Sinking Effect
FrictionInertia
v v v
u v g
x y x
(2) / vdP dy g
 



 
    
2 21
(4) ( , ) ( ) ( )
2
l g
l
g x x
v x y 7/12

8. Laminar Film – First thermodynamics law
 The first law of thermodynamics:
 Substituting conduction & (2):
 Substituting (1)
 Integrating from y=0
 Local mass flow rate:
 Vertical enthalpy inflow:
 Assume linear temperature distribution:
 
   

   
3
0
(1) (y) ( )
3
l
l l v
l
g
vdx

   ,0
(2) [ ( )]l f P l satH v h c T T dx
      ''
(3) 0 ( ) hg wH H dH d q dy

  
'
,
3
[ ( )]
8
(4) ( )
fg
fg P l sat ts
h
a w
l
w h c T T
k
T T dy d
 
 



3
'
( )
(5)
( )
l l sat w
fg l v
kv T T
dy d
h g

 
 
  
  
1/4
'
4 (T T )
(6) ( )
( )
l l sat w
fg l v
kv
y y
h g


 

1sat
sat w
T T x
T T
8/12

9. Laminar flow – Results
 Now we can calculate Heat transfer
coefficients:
 Similar results can be obtained by Scale
Analysis (Similar to laminar boundary
layer natural convection)
 Rohsenow refined preceding analysis by
discarding linear profile assumption and
performing an integral analysis.
 Rohsenow recommends:
 Jacob number = relative measure of
subcooling:
 To summarize:
 

 
    
  
1/43 '''
( )
(1)
4 ( )
l fg l vl
y
sat w l sat w
k h gq k
h
T T yv T T

4
(2)
3
L y Lh h
  
   
 
1/43 '
( )
(3) 0.943
( T )
fg l vL
L
l l l sat w
L h gh L
Nu
k kv T
    '
,(4) 0.68 ( ) (1 0.68 )fgfg p l sat w fgh h c T h JaT

 , ( )
(5) P l sat w
fg
c T T
Ja
h
  '
(6) ( ) ( )l
sat w L
fg
k
L T T Nu
h
  '
(7) ( ) (1 0.68 )fgq L h Ja 9/12

10. Laminar Film - Diagram
 In the preceding analysis were derived
by Nusselt, based on negligible inertia
assumption
 The complete momentum equation used
by Sparrow & Gregg in similarity solution.
 Their solution for Nu falls below Nusselt’s
solution -> Effect of Inertia
 Chen abandoned the assumption of zero
shear at interface, retaining effect of
inertia
 His results for Nu are smaller than Sparrow
& Gregg’s solution -> Effect of restraining
drag of vapor
 Better agreement with experimental data 10/12

11. Turbulent Film - Diagram
 Reynolds number of liquid film:
 Experimental observations:
 Laminar: Re < 30
 Wavy: 30 < Re < 1800
 Turbulent: Re > 1800
 Experiments revealed that heat transfer
rate in wavy and turbulent regions is
considerably larger than laminar section
 Following relation developed by Chen for
wavy and turbulent region:
4
(1) Re (y)y
l
 
  
  
2
1/3 0.44 6 0.8 1.3 1/2
(2) ( ) (Re 5.82 10 Re Pr )
L l
L L L
l
h
k g
11/12

12. Summary
 Condensation is phase change from Gas to Liquid
 There’re different types of condensation:
 Surface (Film, Droplet), Homogeneous, Direct contact
 Film surface condensation has three regions:
 Laminar, Wavy, Turbulent
 Laminar film condensation first solved by Nusselt by neglecting Inertia effect
 Complete momentum equation used by Sparrow and Gregg in similarity solution
 Chen Solution for laminar film contains vapor drag effect and inertia effect of liquid
 Chen reviewed and developed a relation for Wavy and Turbulent regions
12/12

13. Thank you!
13