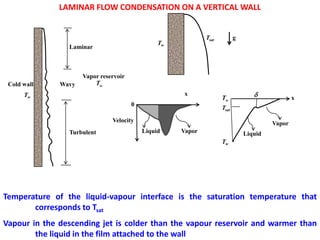
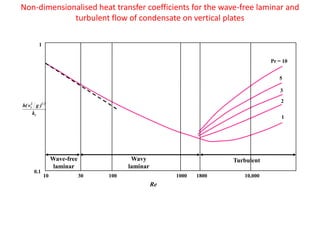
- Condensation occurs when a vapor is cooled and changes phase to a liquid. This happens in power plants, oil refineries, and desalination plants. - Condensation can occur through either film condensation or dropwise condensation. Film condensation involves a liquid film forming on the surface, while dropwise condensation involves discrete liquid droplets. - Dropwise condensation is more efficient with higher heat transfer rates, but is difficult to maintain as the droplet-promoting coating washes off over time. Most condensers are designed for the more conservative film condensation process.

1. Condensation

2. CONDENSERS
Power plant – water is boiled in boiler and condensed in condenser
Oil refinery - oil is evaporated in distillation column and condensed
into liquid fuels like gasoline and kerosene
Desalination plant – water vapor is produced by evaporation from
brine and condensed as pure water
Condensation – enthalpy of phase change to be removed by a coolant
Enthalpy of phase change is relatively large, for water (2.5 106 J/kg)
and associated heat transfer rates are also large
Heat transfer to phase interface – convective process – complicated by
an irregular surface – bubbles and drops

3. CONDENSATION HEAT TRANSFER
• Film condensation
• Dropwise condensation
FILM CONDENSATION
Condensate wets the surface and forms a liquid film
on the surface that slides down under the influence
80° C
of gravity.
Surface is blanketed by a liquid film of increasing
thickness, and this “liquid wall” between the solid
surface and the vapor serves as a resistance to heat
transfer
Liquid film

4. • Condensate film thickness are thin – heat transfer coefficients are large
• Example - steam at a saturation temperature of 305 K condenses on a 2 cm – O.D
tube with a wall temperature of 300 K
•Average film thickness - 50m (0.05 mm) and the average heat transfer coefficient –
11,700 W/m2.K
• If the condensate flow rate is small, the surface of the film will be smooth and the
flow laminar because
• Temperature difference is small
• Wall is short
• If the condensate flow rate is high, waves will form on the surface to give wavy
laminar flow
•If the condensate flow rate is yet higher, the flow becomes turbulent

5. DROPWISE CONDENSATION
80°C
Droplets
If the condensate does not wet the wall, because either it is dirty or it has been
treated with a non-wetting agent, droplets of condensate nucleate at small pits and
other imperfections on the surface, and they grow rapidly by direct vapor
condensation upon them and by coalescence
When the droplets become sufficiently large, they flow down the surface under the
action of gravity and expose bare metal in their tracks, where further droplet
nucleation is initiated
THIS IS CALLED DROPWISE CONDENSATION

6. Droplets slide down when they reach a certain size, clearing the surface and
exposing it to vapor.
There is no liquid film in this case to resist heat transfer.
Heat transfer rates that are more than 10 times larger than those associated with
film condensation can be achieved with dropwise condensation
Most of the heat transfer is through drops of less than 100m diameter
Thermal resistance of such drops is small; hence, heat transfer coefficients for
dropwise condensation are large; values of upto 30000 W/m2.K have been
measured.
Hence, dropwise condensation is preferred over filmwise condensation
Considerable efforts are put for non-wetting heat exchanger surfaces
If the surface is treated with non-wetting agent (stearic acid) to promote dropwise
condensation, the effect lasts only few days, until the promoter is washed off or
oxidised.
Continuous adding of the promoter to the vapour is expensive and contaminates the
condensate.

7. Bonding a polymer such as teflon to the surface is expensive and adds additional
thermal resistance
Gold plating is also expensive
Because of lack of sustainability of dropwise condensation, present day condensers
are designed based on filmwise condensation
Filmwise condensation – conservative estimate

8. LAMINAR FLOW CONDENSATION ON A VERTICAL WALL
Tsat g
Tw
Laminar
Vapor reservoir
Cold wall Wavy T
Tw x
T  x
0
Tsat
Velocity Vapor
Turbulent Liquid Vapor Liquid
Tw
Temperature of the liquid-vapour interface is the saturation temperature that
corresponds to Tsat
Vapour in the descending jet is colder than the vapour reservoir and warmer than
the liquid in the film attached to the wall

9. LAMINAR FLOW CONDENSATION ON A VERTICAL WALL
Consider a vertical wall exposed to a saturated vapour at pressure p and saturation
temperature Tsat = Tsat(P).
The wall could be flat or could be the outside surface of a vertical tube
If the surface is maintained at a temperature Tw < Tsat, vapour will continuously
condense on the wall, and if the liquid phase wets the surface well, will flow
down the wall in a thin film
Provided the condensation rate is not too large, there will be no discernable waves
on the film surface, and the flow in the film will be laminar
• Fluid dynamics of the flow of a thin liquid film
• Heat transfer during the flow of a thin liquid film

10. 0
x
Laminar film of
condensate  x
0
T
Tsat
u
Zero shear , 0
v y
u
Tw
v
x = δ(y)
Interface
T = Tsat
Tsat

Tw x
y H 
y + dy From reservoir of
hg d
saturated vapor
  d
T  Tsat
H + dH

11. ASSUMPTIONS
• Laminar flow and constant properties are assumed for the liquid film
• Gas is assumed to be pure vapour and at a uniform temperature equal to Tsat. The
merit of this simplification is that it allows us to focus exclusively on the
flow of the liquid film and to neglect the movement of the nearest layers of
vapour
• Shear stress at the liquid-vapour interface is assumed to be negligible
• With no temperature gradient in the vapour, heat transfer to the liquid-vapour
interface can occur only by condensation at the interface and not by
conduction from the vapour

12. Steady state two dimensional incompressible flow
 u u  P   2u  2u 
L u  v   
 x   L  2  2 
 y  x  x y 
 v v  P   2v  2v 
L u  v   
 x   L  2  2    L g
 y  y  x y 
x ~ ;y ~ L
u  v , Hence , x  momentum equation vanishes
Neglected, y<<x
 v v  dP  v  v
2 2
L u  v   
 x   L  2  2    L g
 y  dy  x y 
dP
 pressure imposed from the inviscid potion   v g  Hydrostatic pressure
dy
 v v   2v
 L  u  v    L   v g   L 2
 x
 y 
 x

13.  v v   2v
L u  v 
 x   L   v g   L 2
 
 y     
x
  SINKING EFFECT
FRICTION
INERTIA
Assuming inertia is negligible
 2v
 L 2   L   v g  0
x
Boundary conditions x0 v0
v
x  0
x
Integrating v
 L  g   L   v  x  C1
x
x2
 L v  g  L   v   C1 x  C 2
2
x  0 v  0  C2  0
v v
x   0  L  g  L   v x  C1  g  L   v   C1
x x

14. x2
 L v  g  L   v   C1 x  C 2
2
C2  0
C1  g  L   v 
x2
 L v  g   L   v   g   L   v  x
2
g  L   v   x2 
v  x  

L  2 
g  L   v  2 
 x 1  x 2 
vx , y       
L  2  
 
Film thickness is unknown function of (y)

15. Local mass flow rate per unit width  (y)
    y

  y     Lv dx
0
 g  L   v   x 1  x 2 
  y    L  2      dx
L  2  
0
 

g  L   v  2  x 2 1  x 3  
  y   L     3 
L  2 6   
  0
 L g  L   v  2    
  y     
L 2 6
 L g  L   v  2 
  y  
L 3
 L g  L   v   3
  y 
L 3

16.  L g  L   v   3
  y 
L 3
b L g L   v   3
m  b  y  

L 3
B – width of the plate perpendicular to the plane of paper
Flow rate is proportional to the sinking effect - g(L-v)
Flow rate is inversely proportional to the liquid viscosity (Friction)
HEAT TRANSFER PROBLEM
Film velocity is low
Temperature gradients in the y-direction are negligible since both wall and film
surface are isothermal
d 2T
0
dx 2
dT
 C1 ; T  C1 x  C 2
dx

17. T  C1 x  C 2
x   T  Tsat
x  0 T  Tw  C 2  Tw
Tsat  Tw
T  C1 x  Tw  Tsat  C1  Tw  C1 

T  Tsat  Tw 
x
 Tw

This is a linear temperature profile similar to the conduction in a plane
wall

18. Heat flux into the wall = Heat flux across the film
Q k l Tsat  Tw 

 hTsat  Tw   
dT
kl
dx w A 
kl
dT k l Tsat  Tw 
h
dx w
  k
 l
Tsat  Tw  Tsat  Tw  
kl
h

Determination of film thickness
 L g  L   v   b L g L   v   3
m  b  y  
3
  y  ; 
L 3
L 3
 b L g L   v  3 2 d Rate of condensation of
 b  y  
dm
dy L 3 dy vapour over a vertical
distance dy

19. Rate of heat transfer from the vapour = Heat releasead as vapour is condensed
to the plate through the liquid film
  dmh  k b dy Tsat  Tw
dQ  fg l

dm k l b Tsat  Tw


dy h fg 
 b L g  L   v  3 2 d k l b Tsat  Tw
 b  y  
dm

dy L 3 dy h fg 
 L g  L   v  3 2 d k T  Tw
 l sat
L 3 dy h fg 
 L k l Tsat  Tw 
 3 d  dy
 L g  L   v h fg
4  L k l Tsat  Tw 
 yC y  0,   0C  0
4  L g  L   v h fg

20. 4  L k l Tsat  Tw 
 y
4  L g  L   v h fg
1
 4 k 4 T  T  4
  y    L l sat w
y
  L g  L   v h fg 
 
1
  g   L   v h fg k l4  4
h   L
kl 
  4 L k l Tsat  Tw  y 
 
1 1
  L g   
L  L   v h fg k l3  4
 g L  L   v h fg k l3  4 L 1
1
hL   
dy    1
 L
y 4 dy
L 0 4 L Tsat  Tw  y   4 L Tsat  Tw 
    0

21. 1

  
g L  L   v h fg k l3  4

hL  0.943
 4 T  T L 
 L sat w 
1
b L g L   v   3  4 k 4 T  T  4
m  b  y  
   y    L l sat w
y
L 3   L g  L   v h fg 
 
3
b L g  L   v   4 L k l4 Tsat  Tw  4
m
  y
3 L   L g  L   v h fg 
 
All liquid properties evaluated at
Tsat  Tw
Tf 
2

22. Effect of subcooling
Rohsenow refined
• avoided linear temperature profile
• Integral analysis of temperature distribution across the film
Temperature profile whose curvature increases with the degree of subcooling
Cp,L(Tsat-Tw)
h'fg  h fg  0.68C p ,L Tsat  Tw 
Replace in previous equations h fg by h'fg
All liquid properties evaluated at Tsat  Tw
Tf 
2
hfg and v are evaluated at the saturation temperature Tsat

23. JAKOB NUMBER
Is a measure of degree of subcooling experienced by the liquid film
C p ,L Tsat  Tw 
Ja 
h fg
hfg  h fg  0.68C p ,L Tsat  Tw 
hfg  h fg 1  0.68 Ja 

24. Reynolds Number
 L um Dh  4 Ac 4b
Re  ; um  ; Dh    4
L  L P b
 4 4
Re   L 
 L  L  L
4
Re 
L
 L g  L   v   3
  y 
L 3
4 4  L g  L   v   3
Re  
L 3 L L
4  L g 3
2
4 g 3
 L   v  Re  
3 L
2
3 L
2

25. 4  L g 3
2
 L   v  Re 
3 L
2
   x  L  l
kl k
 
h hx  L
3
hx  L  havg
4
3
 
2 
kL 
3
4 g L  k L 
2
4 g L
Re  2 
    

3  L  hx  L  3 L  3
2

 havg 
4 
1
1
  g 3
havg  1.47 k l Re 3 
 2 
 l 

26. Hydraulic diameter
D
P  2L
PL P D Ac  2 L
Ac  L Ac   D 4 Ac
Dh   4
4 Ac P
4A
Dh  c  4 Dh   4
P P

27. Wavy Laminar flow over vertical plates
At Reynolds number greater than about 30, it is observed that waves form at the
liquid vapour interface although the flow in liquid film remains laminar. The flow in
this case is Wavy Laminar
Kutateladze (1963) recommended the following relation for wavy laminar
condensation over vertical plates
1
 g
Re k l 3
hvert ,wavy   
1.08 Re 1.22  2 
 5.2  l 
30  Re  1800 ,  v   l
0.82
 1
 3.70 Lk l Tsat  Tw   g  3 
  
Re vert ,wavy  4.81 
  l hfg  2  
 l 

 


28. Turbulent flow over vertical plates (Re > 1800)
Labuntsov proposed the following relation
1
Re k l  g 3
 
hvert ,turbulent 

8750  58 Pr  0.5 Re 0.75  253   l2 
  
Film condensation on an inclined Plates
hinclined  hvert cos  Condensate

1 1
 1 2
hL   l2  3

kl  g 
 
  Re L0.44 

  3
5.82  10  6 Re L.88 PrL 
0

   

29. Non-dimensionalised heat transfer coefficients for the wave-free laminar and
turbulent flow of condensate on vertical plates
1
Pr = 10
5
3
2
h( vl2 g )1 3
kl
1
Wave-free Wavy Turbulent
laminar laminar
0.1
10 30 100 1000 1800 10,000
Re

30. Problem: Saturated steam at atmospheric pressure condenses on a 2 m high and 3 m
wide vertical plate that is maintained at 80C by circulating cooling water through
the other side. Determine (a) the rate of heat transfer by condensation to the plate
(b) the rate at which the condensate drips off the plate at the bottom
Solution: saturated steam at 1 atm condenses on a vertical plate. The rats of heat
transfer and condensation are to be determined
Assumptions: 1. steady operating conditions exist 2. The plate is isothermal. 3. The
condensate flow is wavy laminar over the entire plate (will be verified). 4. The
density of vapour is much smaller than the density of the liquid v<<l
Properties: The properties of water at the saturation temperature of 100C are hfg =
2257 103 J/g and v = 0.6 kg/m3. The properties of liquid water at the film
temperature 90C are
T  Tw 100  80
T f  sat   90
2 2 hfg  h fg  0.68C p ,L Tsat  Tw 
 l  965 .3 kg / m 3
3
 l  0.315  10 Pa .s hfg  2257 103  0.68 4206 100 80

 l  l  0.326  10  6 m 2 / s
l hfg  2314103 J / kg
C pl  4206 J / kg .K
k l  0.675 W / m .K
Pr  1.9628

31. 1 1
 g     9.81  965 .3  965 .32314  1000 
 v h fg k l3  4 0.675 3  4
 L L   
hL  0.943  0.943 
 4  T  T L   4  0.315  10  3 100  80 4 
 L sat w   
W
hL  2656 .2
m2K
Q  hL As Tsat  Tw   2562 .2  2  3  100  80   307464 W

 
Q  mh  307464  m  2314  10 3  m  0.1329 kg / s
 
sf
4 4 m 4  0.1329 
Re        562.5
L  L  b  0.315  10 3  3 

32. 1 1
 1 2
hL   l2  3

kl  g 
 
  Re L0.44 

  3
5.82  10  6 Re L.88 PrL 
0

   
1 1


hL  0.326  10  
6 2  3 


  562 .5  0.44  
1 2
5.82  10  6  562 .50.88  1.9628 3


0.675 
 9.81   
   
W
hL  7691 .4
m2K
Q  hL As  Tsat  Tw   7691.4  2  3   100  80   2307420 W

 
Q  mhsf  2307420  m  2314  103  m  0.9972 kg / s
 
4 4 m 4  0.9972 
Re    b  0.315  103  3   4221

L L    
This confirms that condensation is in turbulent region
Comments: This Reynolds number confirms that condensation is in Wavy laminar
domain