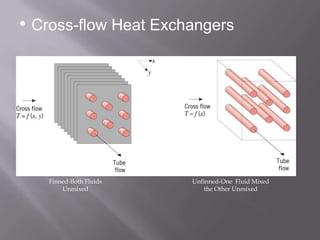
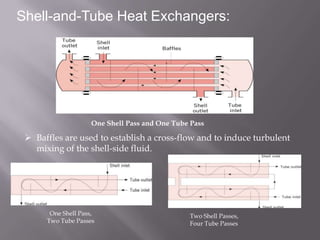
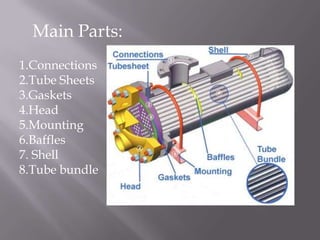
This document discusses heat exchangers and provides details on shell-and-tube heat exchangers. It describes the basic components and design of shell-and-tube heat exchangers, including tubes, tube sheets, baffles, and shells. Equations for heat transfer and thermal analysis of shell-and-tube exchangers are presented. An example problem demonstrates the design calculations to determine the required heat exchanger area and fluid flow rates.

1. Prepared By: Guided By:
Khalasi Bharat K. Dr. Prabhakaran Sir

2.  HEAT EXCHANGER
 Types Of Heat Exchangers
 Shell-and-Tube Heat Exchangers
 Thermal Analysis
 Example
 References

3.  A heat exchanger is a device that is used to
transfer thermal energy between
 two or more fluids,
 a solid surface and a fluid,
 solid particulates and a fluid
 Typical applications involve heating or cooling
of a fluid stream of concern and evaporation or
condensation of single- or multicomponent
fluid streams.

4.  Double-pipe heat exchanger
 Shell and tube heat exchanger
 Plate and frame heat exchanger
 Spiral heat exchanger
 Pipe coil exchanger
 Air-cooled heat exchangers

5. Heat Exchanger Types
• Concentric-Tube Heat Exchangers
Parallel Flow Counterflow

6. • Cross-flow Heat Exchangers
Finned-Both Fluids Unfinned-One Fluid Mixed
Unmixed the Other Unmixed

7. Compact Heat Exchangers
• Achieve large heat rates per unit volume
• Large heat transfer surface areas per unit volume, small flow
passages, and laminar flow.

8. Shell and Tube Heat
Exchangers
• The shell and tube heat exchanger is the most
common style found in industry.
• As the tube-side flow enters the exchanger,
flow is directed into tubes that run parallel to
each other. these tubes run through a shell
that has a fluid passing through it.
• Heat energy is transferred through the tube
wall into the cooler fluid.
• Heat transfer occurs primarily through
conduction and convection.

9. Shell-and-Tube Heat Exchangers:
One Shell Pass and One Tube Pass
 Baffles are used to establish a cross-flow and to induce turbulent
mixing of the shell-side fluid.
One Shell Pass, Two Shell Passes,
Two Tube Passes Four Tube Passes

10. Main Parts:
1.Connections
2.Tube Sheets
3.Gaskets
4.Head
5.Mounting
6.Baffles
7. Shell
8.Tube bundle

11. The Thermal Analysis:
The fundamental equations for heat transfer across a surface are given by:
Q = U A ΔTlm
= w Cp(t) (t2 − t1)
= W Cp(s) (T1 − T2) or W L
Where Q = heat transferred per unit time (kJ/h, Btu/h)
U = the overall heat transfer coefficient (kJ/h-m2 oC, Btu/hft2-ºF)
A = heat-transfer area (m2, ft2)
Δtlm = log mean temperature difference (oC, ºF)
Cp(t) = liquid specific heat tube side,
Cp(s) = liquid specific heat shell side (kJ/kg-ºK, Btu/lb-ºF)
w = tube side flow
W = shell side flow (kg/h, lb/h)
The log mean temperature difference ΔTlm (LMTD) for counter current flow is
given by:

12. • A correction factor is applied to the LMTD to allow for the departure
from true counter current flow to determine the true temperature
difference.
ΔTm = Ft ΔTlm
• The correction factor is a function of the fluid temperatures and the
number of tube and shell passes and
• Correlated as a function of two dimensionless temperature ratios

13. • The correction factor Ft for a 1-2 heat exchanger which has 1
shell pass and 2 or more even number of tube passes is given
by:
• The overall heat transfer coefficient U is the sum of several
individual resistances as follows:
• The combined fouling coefficient hf can be
defined as follows:

14. Area of Flow:
• Shell side cross flow area aS is given by
Spacing Required:
• Spacing does not normally exceed the shell diameter
• Maximum spacing is given by:

15. Shell side Film Coefficient Methods for Single
Component Condensation in Laminar Flow:
• Horizontal condenser sub coolers are less adaptable to rigorous
calculation
• But give considerably higher overall clean coefficients than vertical
condenser sub coolers which have the advantage of well defined
zones.
The Nusselt Method:
• The mean heat transfer coefficient for horizontal condensation
outside a single tube is given by the relationship developed by
Nusselt.
• This correlation takes no account of the influence of vapour flow
which, in addition to the effect of vapour shear, acts to
redistribute the condensate liquid within a tube bundle.

16. The Kern Method:
• Kern adapted the Nusselt equation to allow evaluation of
fluid conditions at the film temperature
• For horizontal tube surfaces from 0° to 180° the above
equation can be further developed to give

17. • McAdam extended the Kern equation to allow for
condensate film and splashing affects.
• The loading per tube is taken to be inversely
proportional to the number tubes to the power of 0.667.
• This equation requires the film to be in streamline
flow
• Reynolds Numbers in range 1800 to 2100

18. Example:
Problem : Design of a two-pass, shell-and-tube heat exchanger to
supply vapour for the turbine of an ocean thermal energy
conversion system based on a standard (Rankine) power
cycle. The power cycle is to generate 2 MW at an
efficiency of 3%. Ocean water enters the tubes of the
exchanger at 300K, and its desired outlet temperature is
292K. The working fluid of the power cycle is evaporated
in the tubes of the exchanger at its phase change
temperature of 290K, and the overall heat transfer
coefficient is known.
FIND: (a) Evaporator area, (b) Water flow rate.
SCHEMATIC:

19. ASSUMPTIONS: (1) Negligible heat loss to surroundings, (2) Negligible kinetic and potential
energy changes, (3) Constant properties.
PROPERTIES: Water ( Tm = 296 K): cp = 4181 J/kg K.
ANALYSIS: (a) The efficiency is

W 2 MW
0.03.
q q
Hence the required heat transfer rate is
2 MW
q 66.7 MW.
0.03
Also
300 290 292 290 C
Tm,CF 5C
300 290
n
292 290
and, with P = 0 and S = , from Fig. it follows that F = 1. Hence

20. q 6.67 107 W
A
U F Tm,CF 1200 W / m 2 K 1 5 C
A 11,100 m2.
b) The water flow rate through the evaporator is
q 6.67 107 W

mh
cp,h Th,i Th,o 4181 J / kg K 300 292

mh 1994 kg / s.
COMMENTS: (1) The required heat exchanger size is enormous due to the small
temperature differences involved,
(2) The concept was considered during the energy crisis of the mid 1970s
but has not since been implemented.

21. REFERANCES:
1. Design And Rating Shell And Tube Heat
Exchangers , By John E. Edwards
2. Engineering Data Book, By Professor John R.
Thome
3. www.pidesign.co.uk
4. en.wikipedia.org

22. THANK YOU

23. Any Question ?