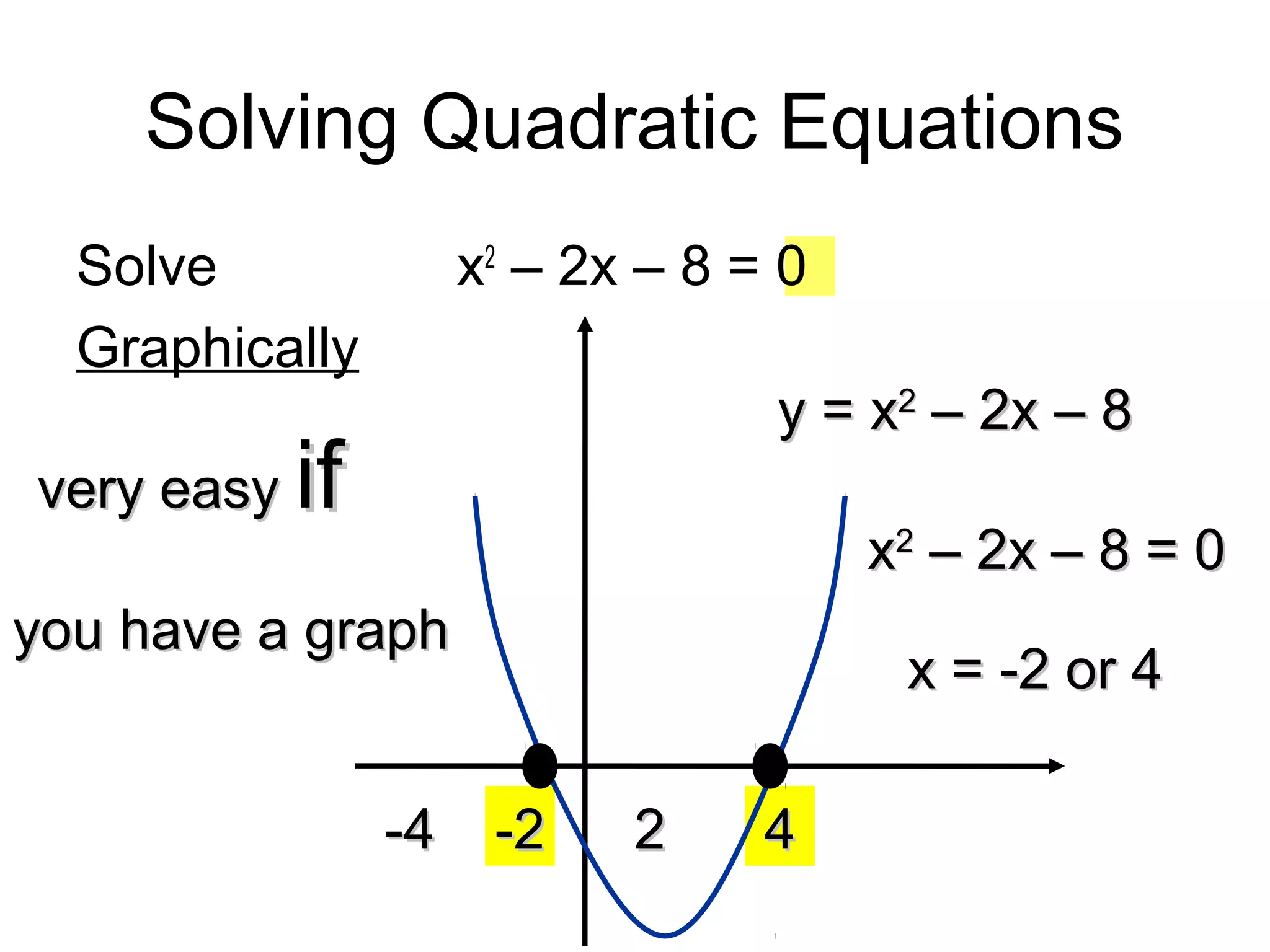
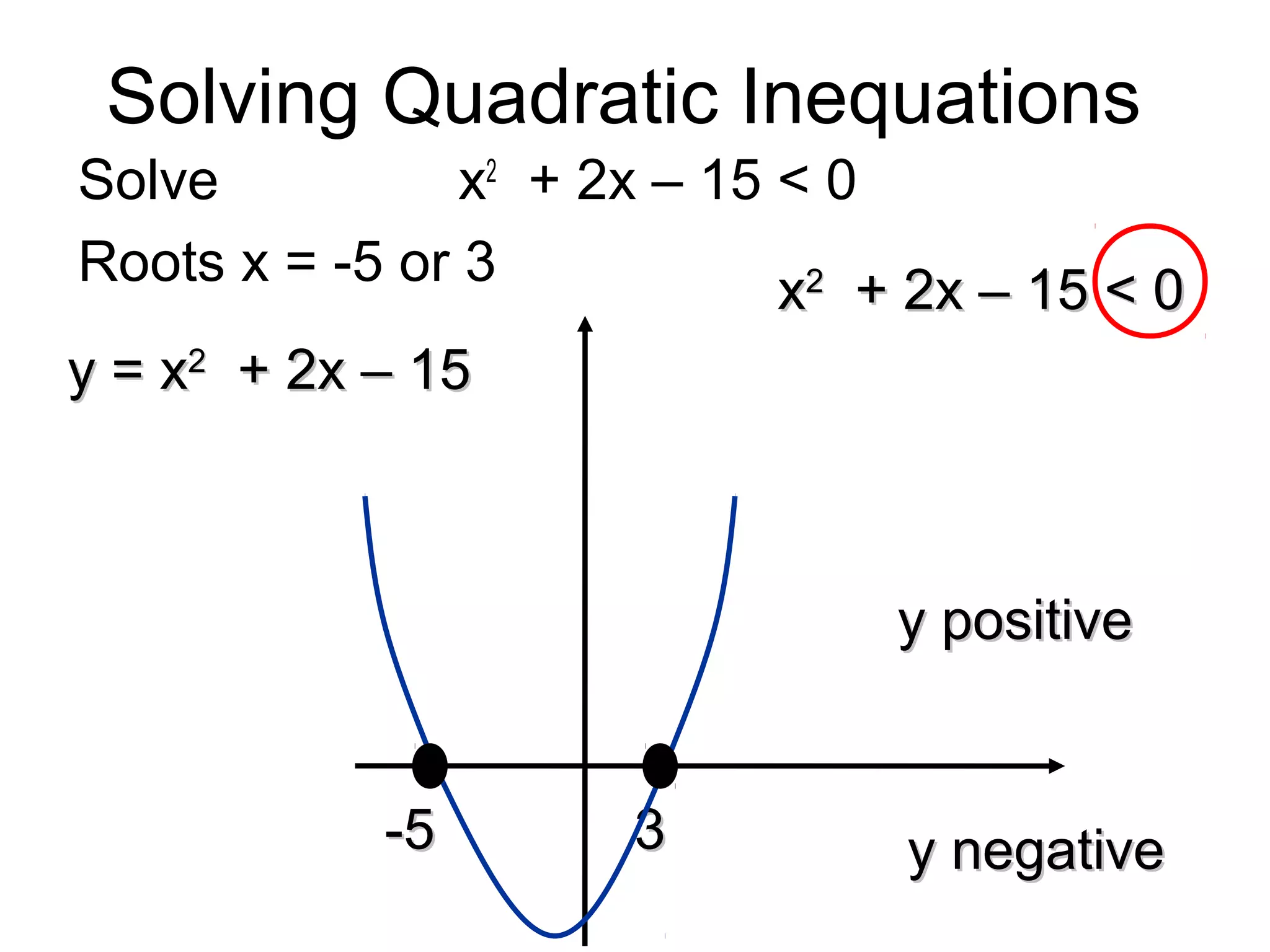
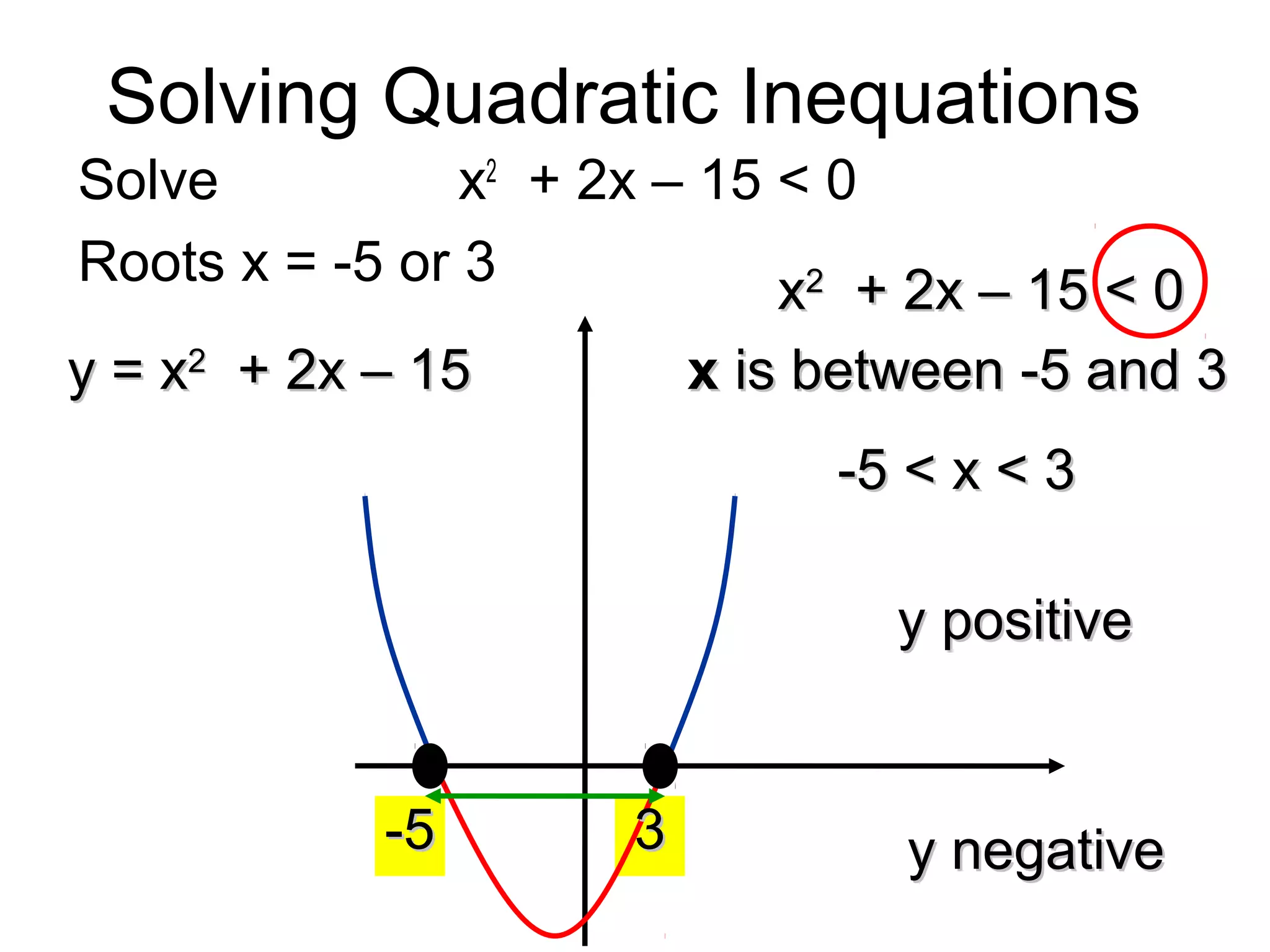
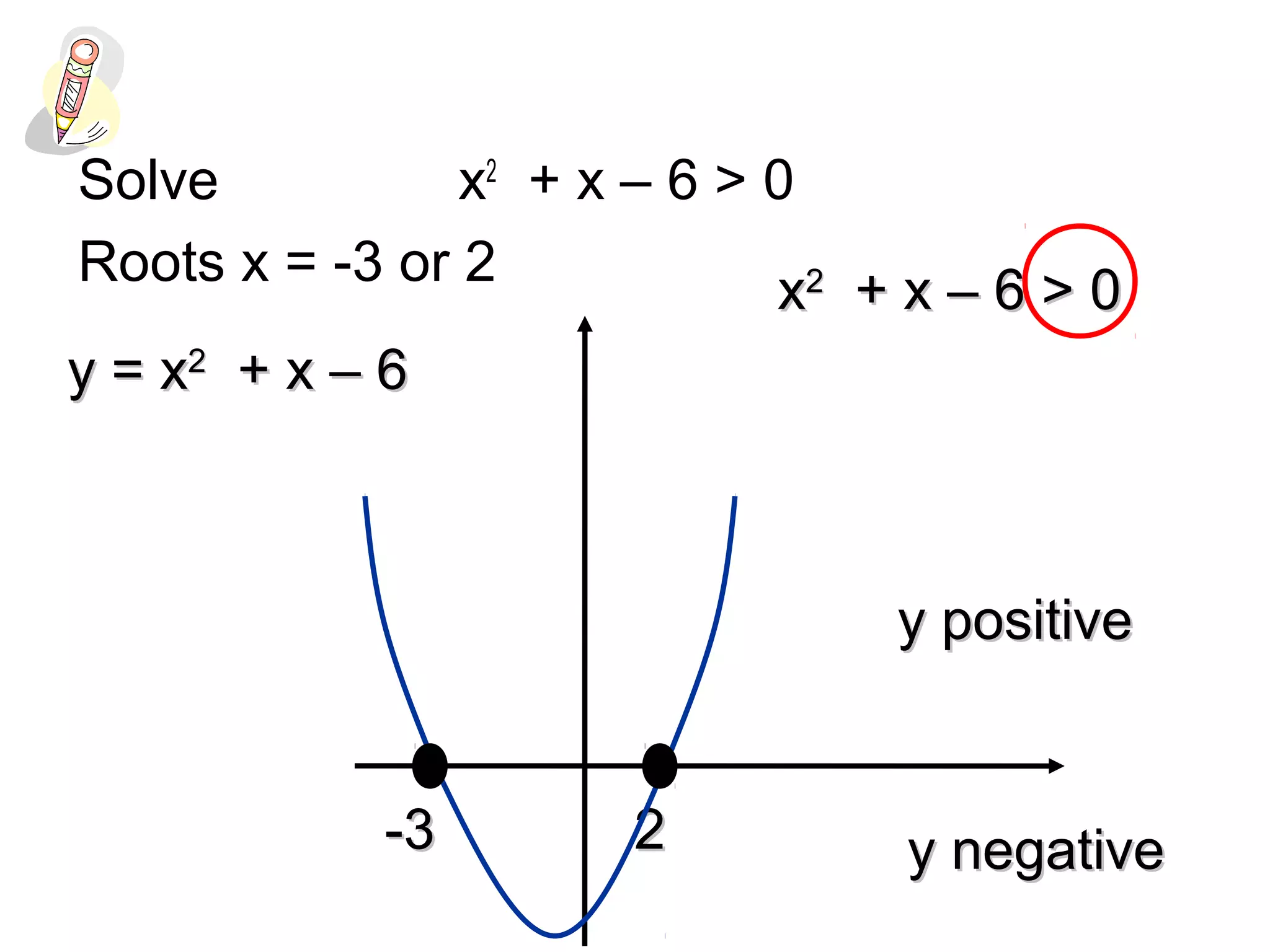
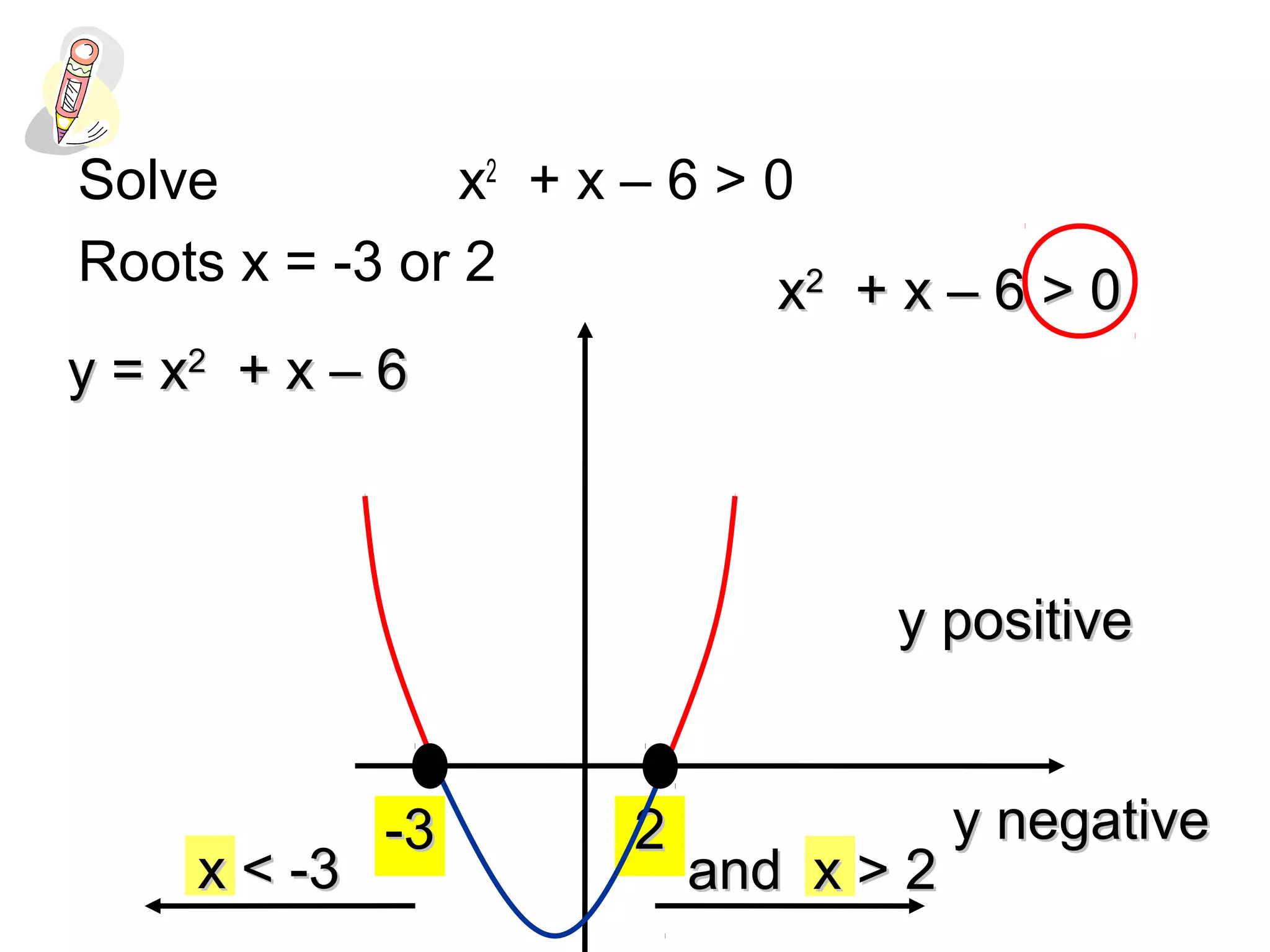
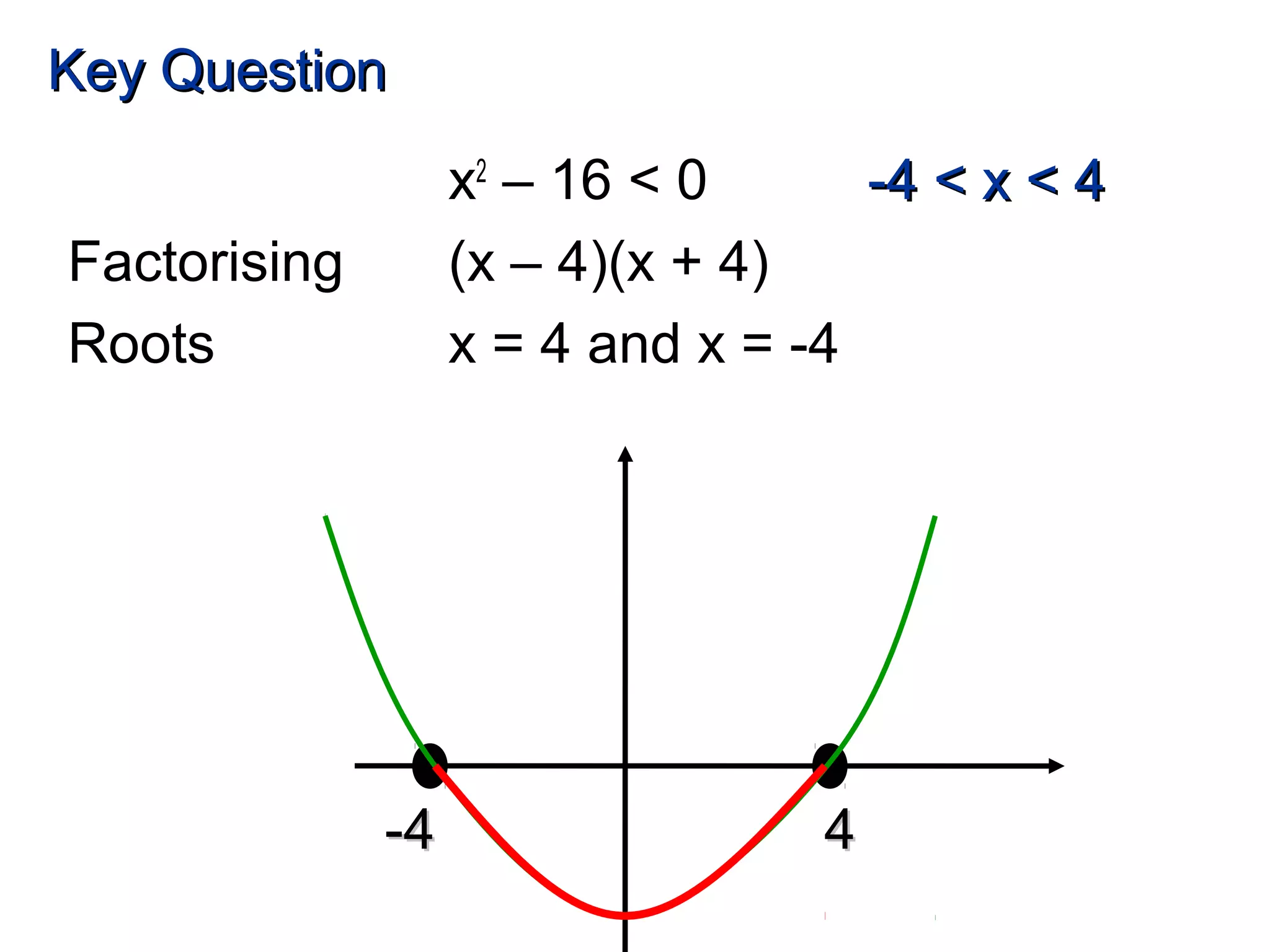
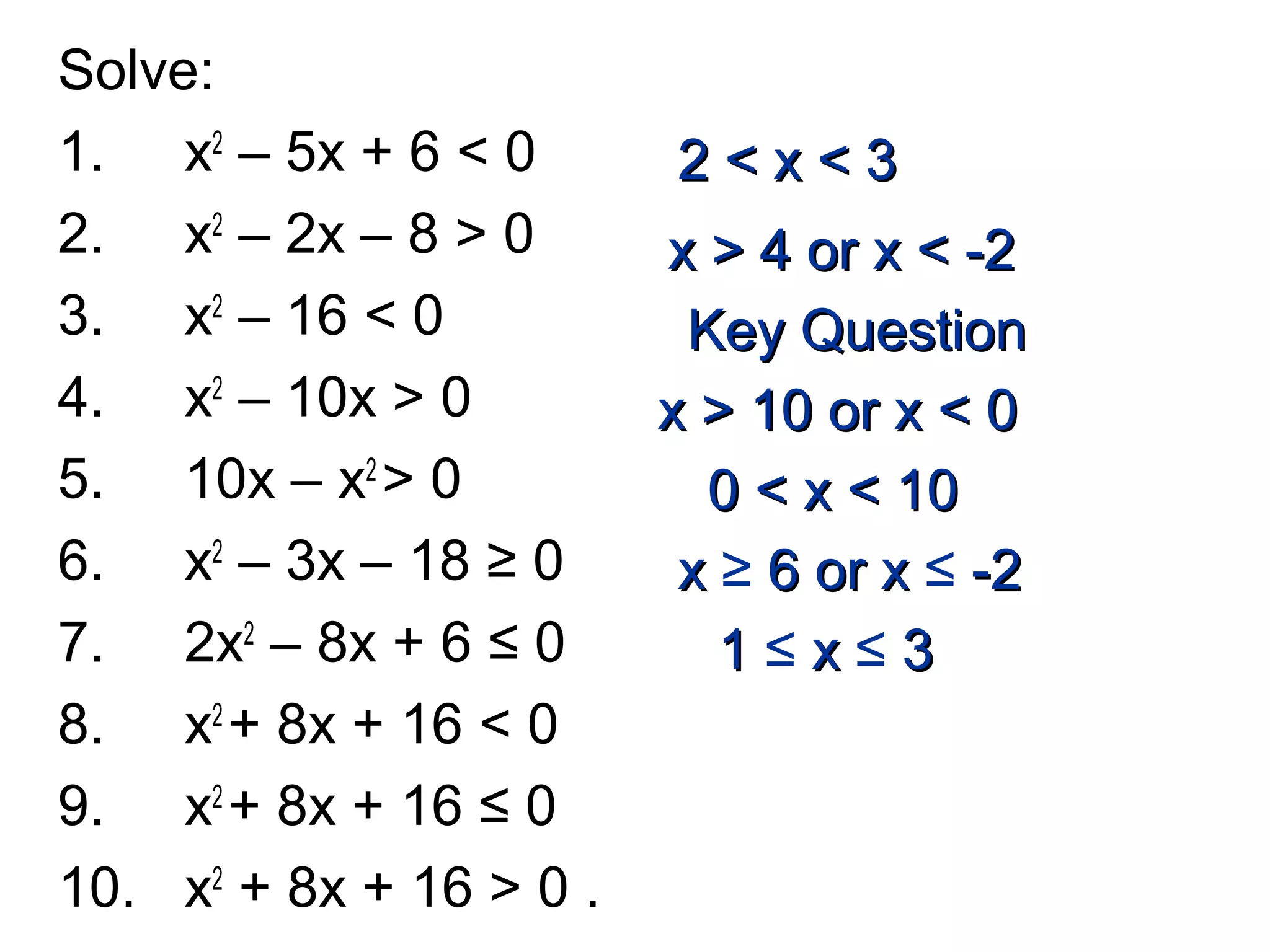This document discusses solving quadratic inequalities by graphing. It explains that the best method is to draw the graph of the quadratic function and find where it is positive and negative based on the roots. The roots are found by factorizing the quadratic expression. Several examples are worked through step-by-step to demonstrate this process. Key questions are provided for students to practice solving various quadratic inequalities graphically.

1. Block 2
Solving Quadratic Inequations

2. What is to be learned?
• The best tactic for solving quadratic
inequations

3. Solving Quadratic Equations
Solve x2
– 2x – 8 = 0
Factorise
(x – 4)(x + 2) = 0
x = 4 or x = -2
Big Nasty Formula
Big L
Trial and Error
Try x = 2 22
– 2(2) – 8 = -8 
Try x = 4  42
– 2(4) – 8 = 0 

4. 22
Solving Quadratic Equations
Solve x2
– 2x – 8 = 0
Graphically
y = xy = x22
– 2x – 8– 2x – 8
-2-2 44-4-4
xx22
– 2x – 8 = 0– 2x – 8 = 0
x = -2 or 4x = -2 or 4
very easyvery easy ifif
you have a graphyou have a graph

5. Graphically is the way to go
Solve x2
+ 2x – 15 < 0
Need graph y = xy = x22
+ 2x – 15+ 2x – 15
Find RootsFind Roots FactoriseFactorise
(x + 5)(x – 3)(x + 5)(x – 3)
roots x=-5 or 3roots x=-5 or 3
Solving Quadratic Inequations

6. 33
Solving Quadratic Inequations
Solve x2
+ 2x – 15 < 0
Roots x = -5 or 3
-5-5
xx22
+ 2x – 15 < 0+ 2x – 15 < 0
y = xy = x22
+ 2x – 15+ 2x – 15
y positivey positive
y negativey negative

7. Solving Quadratic Inequations
Solve x2
+ 2x – 15 < 0
Roots x = -5 or 3
-5-5
xx22
+ 2x – 15 < 0+ 2x – 15 < 0
xx is between -5 and 3is between -5 and 3y = xy = x22
+ 2x – 15+ 2x – 15
y positivey positive
y negativey negative
-5 < x < 3-5 < x < 3
33

8. Solving Quadratic Inequations
Best done by drawing a graph
For graph, need
For roots
rootsroots
FactoriseFactorise

9. Solve x2
+ x – 6 > 0
Need graph y = xy = x22
+ x – 6+ x – 6
Find RootsFind Roots FactoriseFactorise
(x + 3)(x – 2)(x + 3)(x – 2)
roots x= -3 or 2roots x= -3 or 2

10. 22
Solve x2
+ x – 6 > 0
Roots x = -3 or 2
-3-3
xx22
+ x – 6 > 0+ x – 6 > 0
y = xy = x22
+ x – 6+ x – 6
y positivey positive
y negativey negative

11. 22
Solve x2
+ x – 6 > 0
Roots x = -3 or 2
-3-3
xx22
+ x – 6 > 0+ x – 6 > 0
y = xy = x22
+ x – 6+ x – 6
y positivey positive
y negativey negative
x < -3x < -3 and x > 2and x > 2

12. Solve:
1. x2
– 5x + 6 < 0
2. x2
– 2x – 8 > 0
3. x2
– 16 < 0
4. x2
– 10x > 0
5. 10x – x2
> 0
6. x2
– 3x – 18 ≥ 0
7. 2x2
– 8x + 6 ≤ 0
8. x2
+ 8x + 16 < 0
9. x2
+ 8x + 16 ≤ 0
10. x2
+ 8x + 16 > 0 .
2 < x < 32 < x < 3
x > 4 or x < -2x > 4 or x < -2
Key QuestionKey Question
x > 10 or x < 0x > 10 or x < 0
0 < x < 100 < x < 10
xx ≥ 6 or x6 or x ≤ -2-2
11 ≤ xx ≤ 33

13. x2
– 16 < 0
Factorising (x – 4)(x + 4)
Roots x = 4 and x = -4
Key QuestionKey Question
44-4-4
-4 < x < 4-4 < x < 4