1) Completing the square allows quadratic expressions to be written in the form x + a^2 + b. This is useful for solving quadratic equations and finding the turning point of parabolas. 2) To solve the equation x^2 + 4x - 7 = 0 by completing the square: a) Write the expression in the form x + a^2 + b as x + 2^2 - 11 b) Set this equal to 0 and solve for x, obtaining the solutions x = -2 ± √11. 3) Completing the square and writing quadratic expressions in the form x + a^2 + b allows them to be more easily solved and for properties like the

1. GCSE Completing The Square
Dr J Frost (jfrost@tiffin.kingston.sch.uk)
www.drfrostmaths.com
@DrFrostMaths
Last modified: 5th March 2018

2. 𝑥 + 1 2
= 𝑥2
+ 𝟐𝑥 + 1
𝑥 + 3 2
= 𝑥2
+ 𝟔𝑥 + 9
𝑥 − 4 2
= 𝑥2
− 𝟖𝑥 + 16
𝑥 + 𝑎 2
= 𝑥2
+ 𝟐𝒂𝑥 + 𝑎2
Expand the following brackets.
Do you notice any relationship between the original expression
and coefficient of 𝑥 in the expanded expression in each case?
Starter
Key Term: The coefficient of a term
is the number on front of it. So the
coefficient of 3𝑥 is 3 and the
coefficient of 5𝑥2
is 5.
?
?
?
?
The coefficient of 𝒙 is double the number after the 𝒙 in the bracket.
? Relationship

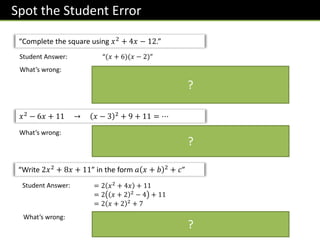
3. Therefore…
Therefore, it seems as if we can halve the coefficient of 𝒙 to get the
missing number in 𝑥 + __ 2
𝑥2
+ 10𝑥 → 𝑥 + 5 2
− 25
Consider the expansion of 𝑥 + 5 2
:
𝑥 + 5 2
= 𝑥2
+ 10𝑥 + 25
We only want the “𝑥2
+ 10𝑥” so we
‘throw away’ the 25 by subtracting it.
𝑥2 + 8𝑥 → 𝑥 + 4 2 − 16
𝑥2
+ 2𝑥 → 𝑥 + 1 2
− 1
𝑥2 + 𝑥 → 𝑥 +
1
2
2
−
1
4
Put the following in the form 𝑥 + 𝑎 2 + 𝑏
Because the form required was
“ 𝑥 + 𝑎 2
+ 𝑏”, we might expect to
have to write our answer as:
𝑥 + 5 2
+ [−25]
However, since this is effectively the
same as 𝑥 + 5 2
− 25, this form is
preferred; it is cleaner!
𝑥2 − 6𝑥 → 𝑥 − 3 2 − 9 Because of the − sign, you might be
tempted to think that the answer is
𝑥 − 3 2
+ 9. But note that:
𝑥 − 3 2
= 𝑥2
− 6𝑥 + 9
We don’t want the +9, so we subtract
just as before.
𝑥2 − 20𝑥 → 𝑥 − 10 2 − 100
𝑥2 − 12𝑥 → 𝑥 − 6 2 − 36
?
?
?
?
?
?
?

4. Further Examples
! Putting a quadratic expression in the form 𝑥 + 𝑎 2 + 𝑏 is known as
‘completing the square’.
The key motivation is that while 𝑥2
+ 4𝑥 + 9 contains an 𝑥2
term and a 𝑥
term, its ‘completed square’ 𝑥 + 2 2 + 5 only contains a single 𝒙. We will see
later why this has a number of useful applications.
Put the following in the form 𝑥 + 𝑎 2
+ 𝑏
𝑥2 + 8𝑥 + 3 → 𝑥 + 4 2 − 16 + 3
= 𝑥 + 4 2 − 13
The +3 is still there!
𝑥2 − 2𝑥 + 10 → 𝑥 − 1 2 − 1 + 10
= 𝑥 + 4 2 + 9
𝑥2
+ 12𝑥 − 1 → 𝑥 + 6 2
− 36 − 1
= 𝑥 + 4 2 − 37
𝑥2
− 𝑥 + 1 → 𝑥 −
1
2
2
−
1
4
+ 1 = 𝑥 −
1
2
2
+
3
4
?
?
?
?

5. Test Your Understanding
Put the following in the form 𝑥 + 𝑎 2 + 𝑏
𝑥2 + 16𝑥 → 𝑥 + 8 2 − 16
𝑥2 + 10𝑥 + 31 → 𝑥 + 5 2 − 25 + 31
= 𝑥 + 5 2 + 6
𝑥2 − 6𝑥 − 5 → 𝑥 − 3 2 − 9 − 5
= 𝑥 − 3 2 − 14
?
?
?

6. Exercise 1
N
1
Put the following in the form 𝑥 + 𝑎 2 + 𝑏
a
b
𝑥2 + 20𝑥 = 𝒙 + 𝟏𝟎 𝟐 − 𝟏𝟎𝟎
𝑥2 − 2𝑥 = 𝒙 − 𝟏 𝟐 − 𝟏
𝑥2 + 4𝑥 − 1 = 𝒙 + 𝟐 𝟐 − 𝟓
𝑥2 + 6𝑥 + 3 = 𝒙 + 𝟑 𝟐 − 𝟔
𝑥2 − 2𝑥 + 5 = 𝒙 − 𝟏 𝟐 + 𝟒
𝑥2
− 10𝑥 − 2 = 𝒙 − 𝟓 𝟐
− 𝟐𝟕
𝑥2 + 20𝑥 + 100 = 𝒙 + 𝟏𝟎 𝟐
𝑥2
− 8𝑥 + 1 = 𝒙 − 𝟒 𝟐
− 𝟏𝟓
𝑥2
+ 3𝑥 = 𝒙 +
𝟑
𝟐
𝟐
−
𝟗
𝟒
𝑥2
− 5𝑥 + 1 = 𝒙 −
𝟓
𝟐
𝟐
−
𝟐𝟏
𝟒
c
d
e
f
g
2 a
b
h
𝑥2 + 𝑎𝑥 = 𝒙 +
𝒂
𝟐
𝟐
−
𝒂𝟐
𝟒
𝑥2
+ 2𝑎𝑥 + 𝑎2
= 𝒙 + 𝒂 𝟐
a
b
?
?
?
?
?
?
?
?
?
?
?
?
3 𝑥2
+ 7𝑥 + 2 = 𝒙 +
𝟕
𝟐
𝟐
−
𝟒𝟏
𝟒
𝑥2
− 𝑥 + 3 = 𝒙 −
𝟏
𝟐
𝟐
+
𝟏𝟏
𝟒
𝑥2
−
1
3
𝑥 +
1
4
= 𝒙 −
𝟏
𝟔
𝟐
+
𝟐
𝟗
a
b
c
?
?
?

7. What if the coefficient of 𝑥2
is not 1?
Put 2𝑥2
+ 8𝑥 + 7 in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
2 𝑥2 + 4𝑥 + 7
= 2 𝑥 + 2 2
− 4 + 7
= 2 𝑥 + 2 2 − 8 + 7
= 2 𝑥 + 2 2 − 1
Factorise the coefficient of 𝑥2
out of the first two
terms (leave last term outside brackets)
?
? Complete the square within brackets
(you should have a bracket within a bracket)
Expand outer bracket
Final simplification.
?
?
Put 3𝑥2 − 6𝑥 + 11 in the form
𝑎 𝑥 + 𝑏 2 + 𝑐
3 𝑥2 − 2𝑥 + 11
= 3 𝑥 − 1 2 − 1 + 11
= 3 𝑥 − 1 2 − 3 + 11
= 3 𝑥 − 1 2 + 8
Put 4𝑥2 + 40𝑥 − 5 in the form
𝑎 𝑥 + 𝑏 2 + 𝑐
4 𝑥2
− 2𝑥 + 11
= 4 𝑥 − 1 2 − 1 + 11
= 4 𝑥 − 1 2
− 4 + 11
= 4 𝑥 − 1 2 + 7
? ?

8. Harder Examples
Put 3 − 12𝑥 − 𝑥2
in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
−1𝑥2 − 12𝑥 + 3
= −1 𝑥2 + 12𝑥 + 3
= −1 𝑥 + 6 2 − 36 + 3
= − 𝑥 + 6 2 + 36 + 3
= − 𝑥 + 6 2 + 39 𝑜𝑟 39 − 𝑥 + 6 2
?
Put
1
10
𝑥2
+ 4𝑥 − 3 in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
=
1
10
𝑥2
+ 40𝑥 − 3
=
1
10
𝑥 + 20 2 − 400 − 3
=
1
10
𝑥 + 20 2
− 40 − 3
=
1
10
𝑥 + 20 2
− 43
?

9. Test Your Understanding
Put 5𝑥2
+ 20𝑥 + 7 in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
Put
1
4
𝑥2
− 3𝑥 + 7 in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
= 5 𝑥2 + 4𝑥 + 7
= 5 𝑥 + 2 2 − 4 + 7
= 5 𝑥 + 2 2
− 20 + 7
= 5 𝑥 + 2 2
− 13
=
1
4
𝑥2
− 12𝑥 + 7
=
1
4
𝑥 − 6 2 − 36 + 7
=
1
4
𝑥 − 6 2 − 9 + 7
=
1
4
𝑥 − 6 2 − 2
?
?

10. Exercise 2
1
Put the following in the form 𝑎 𝑥 + 𝑏 2 + 𝑐
a 3𝑥2
+ 6𝑥 − 2 = 𝟑 𝒙 + 𝟏 𝟐
− 𝟓
2𝑥2 − 12𝑥 + 1 = 𝟐 𝒙 − 𝟑 𝟐 − 𝟏𝟕
4𝑥2
− 40𝑥 + 11 = 𝟒 𝒙 − 𝟓 𝟐
− 𝟖𝟗
2𝑥2
+ 24𝑥 + 70 = 𝟐 𝒙 + 𝟔 𝟐
− 𝟐
5𝑥2 − 60𝑥 + 10 = 𝟓 𝒙 − 𝟔 𝟐 − 𝟏𝟕𝟎
3𝑥2
+ 12𝑥 − 1 = 𝟑 𝒙 + 𝟐 𝟐
− 𝟏𝟑
b
c
d
e
f
2 a −𝑥2 + 8𝑥 + 6 = − 𝒙 − 𝟒 𝟐 + 𝟐𝟐
−𝑥2
− 10𝑥 + 5 = − 𝒙 + 𝟓 𝟐
+ 𝟑𝟎
−𝑥2
+ 6𝑥 − 2 = − 𝒙 − 𝟑 𝟐
+ 𝟕
1 − 2𝑥 − 𝑥2 = − 𝒙 + 𝟏 𝟐 + 𝟐
−2𝑥2
+ 12𝑥 − 20 = −𝟐 𝒙 − 𝟑 𝟐
− 𝟐
5 + 10𝑥 − 5𝑥2
= −𝟓 𝒙 − 𝟏 𝟐
+ 𝟏𝟎
b
c
d
e
f
3 a
1
3
𝑥2
+ 2𝑥 + 1 =
𝟏
𝟑
𝒙 + 𝟑 𝟐
− 𝟐
1
5
𝑥2
− 4𝑥 + 13 =
𝟏
𝟓
𝒙 − 𝟏𝟎 𝟐
− 𝟕
1
6
𝑥2 + 𝑥 − 1 =
𝟏
𝟔
𝒙 + 𝟑 𝟐 −
𝟓
𝟐
b
c
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?

11. Why complete the square?
There are 3 major applications of completing the square, two of which we will look at:
1 :: Solving Equations
“(a) Write 𝑥2
+ 4𝑥 − 7 in the form 𝑥 + 𝑎 2
+ 𝑏.
(b) Hence determine the exact solutions of:
𝑥2
+ 4𝑥 − 7 = 0
Solving quadratic equations in this way also allows us to derive
the quadratic formula! (The proof is later in these slides)
2 :: Finding the Turning
Point of a Parabola
“Determine the turning point of the line with equation
𝑦 = 𝑥2 − 4𝑥 + 5”
Key Term: A parabola is the name of a line
which has a quadratic equation.
3 :: (Further Maths A Level)
Integrating reciprocals of
quadratics
“Determine
1
𝑥2−4𝑥+5
𝑑𝑥”
means “integrate”. This allows us to find
the area under a graph. You won’t need to
worry about this for some time!

12. Application #1 :: Solving by Completing the Square
a) Write 𝑥2
+ 4𝑥 − 7 in the form 𝑥 + 𝑎 2
+ 𝑏
b) Hence, determine the exact solutions of 𝑥2 + 4𝑥 − 7 = 0
𝑥 + 2 2 − 4 − 7
= 𝑥 + 2 2
− 11
𝑥 + 2 2
− 11 = 0
𝑥 + 2 2
= 11
𝑥 + 2 = ± 11
𝑥 = −2 ± 11
Because 𝑥 now only appears once in the
equation, we can use our ‘changing the
subject’ skills to make 𝑥 the subject.
Don’t forget the ±. Suppose for example we were
solving 𝑥2
= 4. 𝑥 = ±2 because 22
= 4 and −2 2
= 4
We tend to write 𝑎 ± 𝑏 rather than ± 𝑏 + 𝑎 to avoid
ambiguity of what is included under the √.
?
a
b
?
?
?

13. Further Examples
a) Write 𝑥2
− 6𝑥 + 3 in the form 𝑥 + 𝑎 2
+ 𝑏
b) Hence, determine the exact solutions of 𝑥2 − 6𝑥 + 3 = 0
𝑥 − 3 2 − 9 + 3 = 0
𝑥 − 3 2
− 6 = 0
𝑥 − 3 2
= 6
𝑥 − 3 = ± 6
𝑥 = 3 ± 6
a) Write 2𝑥2
+ 8𝑥 − 1 in the form 𝑎 𝑥 + 𝑏 2
+ 𝑐
b) Hence, determine the exact solutions of 2𝑥2
+ 8𝑥 + 1 = 0
2 𝑥2
+ 4𝑥 − 1
= 2 𝑥 + 2 2
− 4 − 1
= 2 𝑥 + 2 2
− 8 − 1
= 2 𝑥 + 2 2
− 9
2 𝑥 + 2 2
− 9 = 0
2 𝑥 + 2 2
= 9
𝑥 + 2 2
=
9
2
𝑥 + 2 = ±
3
2
𝑥 = −2 ±
3 2
2
?
?

14. Test Your Understanding
a) Write 𝑥2
+ 10𝑥 − 4 in the form 𝑥 + 𝑎 2
+ 𝑏
b) Hence, determine the exact solutions of 𝑥2 + 10𝑥 − 4 = 0
𝑥 + 5 2
− 29 = 0
𝑥 + 5 = ± 29
𝑥 = −5 ± 29
a) Write 3𝑥2 − 30𝑥 + 71 in the form 𝑎 𝑥 + 𝑏 2 + 𝑐
b) Hence, determine the exact solutions of 3𝑥2
− 30𝑥 + 11 = 0
3 𝑥2 − 10𝑥 + 71
= 3 𝑥 − 5 2
− 25 + 71
= 3 𝑥 − 5 2 − 75 + 71
= 3 𝑥 − 5 2 − 4
3 𝑥 − 5 2
− 4 = 0
𝑥 − 5 2
=
4
3
𝑥 − 5 = ±
2
3
𝑥 = 5 ±
2 3
3
?
?

15. Application #2 :: Minimum/Maximum Values
For the quadratic expression 𝑥2
− 4𝑥 + 11,
(a) Determine its minimum value.
(b) Determine the value of 𝑥 for which this minimum occurs.
Completing the square also allows us to find the minimum or maximum
value of a quadratic.
𝑥 − 2 2
− 4 + 11
= 𝑥 − 2 2 + 7
First complete the square.
Let’s experiment with different values of 𝑥 to see what gives us the smallest value:
𝑥 = 0 → 0 − 2 2
+ 7 = 11
𝑥 = 1 → 1 − 2 2
+ 7 = 8
𝑥 = 2 → 2 − 2 2
+ 7 = 7
𝑥 = 3 → 32 2
+ 7 = 8
So the minimum value of 𝑥2
− 4𝑥 + 11 appears to be 7, which occurs when 𝑥 = 2.
But why is this?
Anything squared is at least 0. So we choose 𝒙 such that the squared term is 0 in
order to minimise it.
?
?
?
?
?
? ?
?

16. Further Examples
For the quadratic expression 𝑥2
+ 6𝑥 + 5,
(a) Determine its minimum value.
(b) Determine the value of 𝑥 for which this minimum occurs.
= 𝑥 + 3 2 − 9 + 5
= 𝑥 + 3 2
− 4
We want the squared term to be 0. This occurs when
𝑥 = −3. Then the minimum value will be
02
− 4 = −4
! The minimum
value of 𝑥 + 𝑎 2 + 𝑏
is 𝑏, which occurs
when 𝑥 = −𝑎.
?
For the quadratic expression −𝑥2
+ 8𝑥 + 3,
(a) Determine its maximum value.
(b) Determine the value of 𝑥 for which this maximum occurs.
= − 𝑥2
− 8𝑥 + 3
= − 𝑥 − 4 2
− 16 + 3
= − 𝑥 − 4 2
+ 19
= 19 − 𝑥 − 4 2
We are subtracting a number which is at least 0. Therefore to
maximise the result, we should subtract 0.
Max value: 19 𝑥 at which this occurs: 4
?

17. Turning Points of Quadratics
𝑃
A curve with equation 𝑦 = 𝑥2
− 8𝑥 + 17
has a turning point at 𝑃. Determine the
coordinates of 𝑃.
At the turning point, the value of 𝑦, i.e. 𝑥2
− 8𝑥 + 17, is
minimised. We know how to do this!
𝑦 = 𝑥 − 4 2
− 16 + 17
= 𝑥 − 4 2 + 1
∴ 𝑃(4,1)
?
Quickfire Questions
𝑦 = 𝑥2
+ 2𝑥 + 8 = 𝑥 + 1 2
+ 7 −1,7
𝑦 = 𝑥2 − 6𝑥 + 3 = 𝑥 − 3 2 − 6 3, −6
𝑦 = 𝑥2
+ 10𝑥 + 4 = 𝑥 + 5 2
− 21 −5, −21
𝑦 = 2𝑥2
+ 8𝑥 + 1 = 2 𝑥 + 2 2
− 7 (−2, −7)
Completed Square Turning Point
? ?
? ?
? ?
? ?

18. Test Your Understanding
𝒚 = 𝒙 + 𝟓 𝟐
− 𝟕
−𝟓, −𝟕
= 𝒙 − 𝒎 𝟐
− 𝒎𝟐
Minimum value: −𝒎𝟐
(which occurs when 𝒙 = 𝒎)
?
?

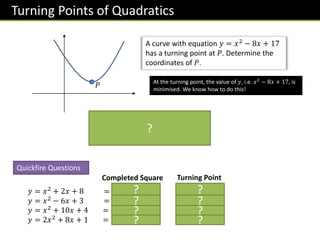
19. Exercise 3
Find the turning point of the curves
with the following equations:
𝑦 = 𝑥2
+ 6𝑥 + 1 −𝟑, −𝟖
𝑦 = 𝑥2 − 4𝑥 + 13 𝟐, 𝟗
𝑦 = 𝑥2
+ 10𝑥 + 31 −𝟓, 𝟔
𝑦 = 𝑥2 − 12𝑥 + 30 𝟔, −𝟔
𝑦 = 3𝑥2
+ 12𝑥 + 1 −𝟐, −𝟏𝟏
𝑦 = 2𝑥2 − 12𝑥 + 21 𝟑, 𝟑
𝑦 = 8 − 4𝑥 − 𝑥2
−𝟐, 𝟏𝟐
𝑦 = 1 − 8𝑥 − 2𝑥2
−𝟐, 𝟗
Find the minimum value of the
following expressions:
𝑥2
+ 2𝑥 + 2 𝟏
𝑥2
+ 10𝑥 + 4 − 𝟐𝟏
𝑥2 − 4𝑥 + 7 𝟑
𝑥2
+ 𝑥 + 2
𝟕
𝟒
𝑥2
+ 𝑎𝑥 − 𝒂𝟐
1
a
b
c
d
e
f
g
h
2
a
b
c
d
e
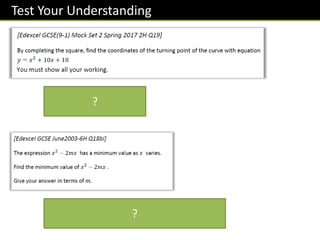
[Edexcel GCSE(9-1) Mock Set 1 Autumn 2016 -
1H Q15]
Here is a sketch of a vertical cross section through the
centre of a bowl.
The cross section is the shaded region between the
curve and the 𝑥 -axis.
The curve has equation 𝑦 =
𝑥2
10
− 3𝑥 where 𝑥 and 𝑦
are both measured in centimetres.
Find the depth of the bowl.
𝒚 =
𝟏
𝟏𝟎
𝒙𝟐
− 𝟑𝟎𝒙
=
𝟏
𝟏𝟎
𝒙 − 𝟏𝟓 𝟐
− 𝟐𝟐𝟓
=
𝟏
𝟏𝟎
𝒙 − 𝟏𝟓 𝟐
− 𝟐𝟐. 𝟓
Minimum point is 𝟏𝟓, −𝟐𝟐. 𝟓
Therefore depth is 22.5 cm
?
?
?
?
?
?
?
?
?
?
?
?
?
?
3

20. Spot the Student Error
“Complete the square using 𝑥2 + 4𝑥 − 12.”
Student Answer: “(𝑥 + 6)(𝑥 − 2)”
What’s wrong: The student factorised rather than completed the square.
• We factorise when we want to find the roots of a quadratic.
• Meanwhile, we complete the square when we want to find the
turning point of a quadratic.
𝑥2 − 6𝑥 + 11 → 𝑥 − 3 2 + 9 + 11 = ⋯
What’s wrong: The 9 should have been subtracted (and it should always be a
subtraction regardless of whether the coefficient of 𝑥 is positive or
negative.
“Write 2𝑥2 + 8𝑥 + 11” in the form 𝑎 𝑥 + 𝑏 2 + 𝑐”
Student Answer: = 2 𝑥2
+ 4𝑥 + 11
= 2 𝑥 + 2 2
− 4 + 11
= 2 𝑥 + 2 2
+ 7
What’s wrong: In the last line of working, they did −4 + 11 → +7
They forgot to multiply the −4 by 2.
?
?
?

21. Proof of the Quadratic Formula
By completing the square, show that the solution of 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0 is
𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
𝑥2 +
𝑏
𝑎
𝑥 +
𝑐
𝑎
= 0
𝑥 +
𝑏
2𝑎
2
−
𝑏2
4𝑎2
+
𝑐
𝑎
= 0
𝑥 +
𝑏
2𝑎
2
=
𝑏2
4𝑎2 −
𝑐
𝑎
=
𝑏2
− 4𝑎𝑐
4𝑎2
𝑥 +
𝑏
2𝑎
= ±
𝑏2 − 4𝑎𝑐
4𝑎2
= ±
𝑏2 − 4𝑎𝑐
2𝑎
𝑥 = −
𝑏
2𝑎
±
𝑏2 − 4𝑎𝑐
2𝑎
=
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
?