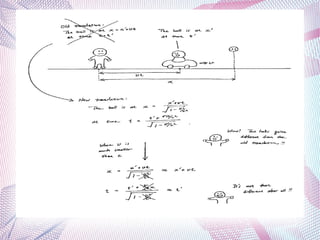
The document discusses Lorentz transformations, which relate the space and time coordinates between frames of reference moving at constant velocities. It states that Lorentz transformations supersede Galilean transformations by accounting for velocities close to the speed of light. The key equations for Lorentz transformations and their inverse are presented, along with an example showing how the transformations ensure light speed remains constant between frames.

1. CONTENT:
➢ Lorentz Transformation
➢ Superseding of Lorentz Transformation to Galilean
Transformation
➢ Inverse Lorentz Transformation
➢ Relativity Equations

2. LORENTZ
TRANSFORMATION
The set of equations which in Einstein's special
theory of relativity relate the space and time
coordinates of one frame of reference to those of
other.
Or,
The Lorentz transformation are coordinate
transformations between two coordinate frames that
move at constant velocity relative to each other.
Note: The 'Lorentz Transformations' only refers
to transformations between inertial frames,
usually in the context of special relativity.
The transformations are named after the Dutch
Physicist Hendrik Lorentz

3. Superseding of Lorentz Transformation to Galilean
Transformation
Lorentz transformation supersede(replace) the
Galilean transformation of Newtonian physics, which
assumes an absolute space and time. The Galilean
transformation is a good approximation only at relative
speeds much smaller than the speed of light.
What Einstein's special theory of relativity says is that
to understand why the speed of light is constant, we
have modify the way in which we relate the
observation in one inertial frame to that of another.
The Galilean transformation is,
x'=x-vt, t'=t
which is wrong. The correct relation is,

4. These are called the Lorentz transformation of space and
time respectively.

6. We can see that if the relative velocity v between the two
frames are much smaller than the speed of light c, then
the ratio v/c can be neglected in this relation and we
recover the Galilei transformation. So the reason why we
did not have any problems with the Galilei transformation
up to now is that v was small enough for it to be good
approximation of the Lorentz transformation.
Let's check that this relation does indeed show that the
speed of light is same in both frames (x,t) and (x',t'). Let's
say that a beam of light started out from the origin x'=x=0
at time t'=t=0. Since the speed of light is c,at time t=T,
the beam of light would have travelled to the point x=cT
in the (x,t) frame. In the other frame, this point is
observed as,

7. So the speed of light in the (x',t') frame would also be:

8. Inverse Lorentz
Transformation
If we want to transform the coordinates from system S to
S', then the transformation equations are :
(Replace v by -v)
These equations are known as Inverse Lorentz
Transformation

9. Relativity
Equations

10. Relativity
Equations