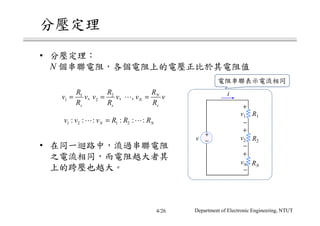
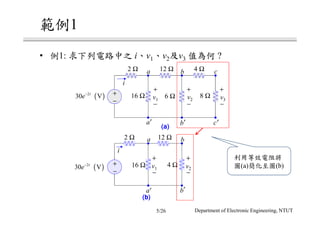
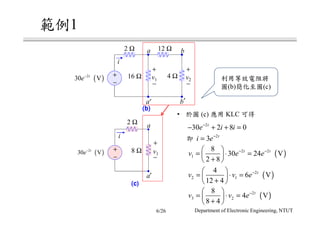
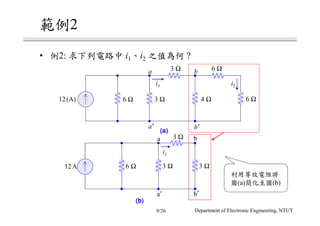
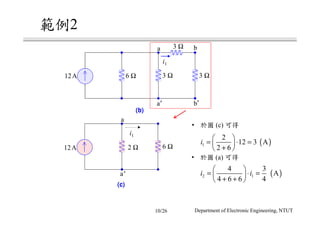
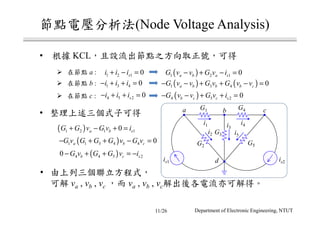
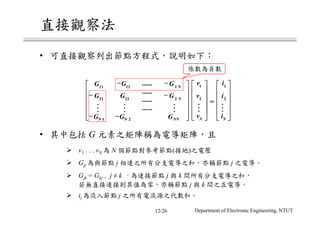
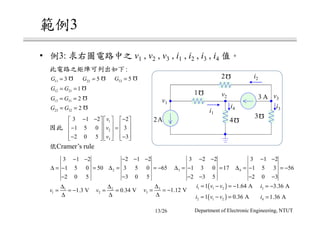
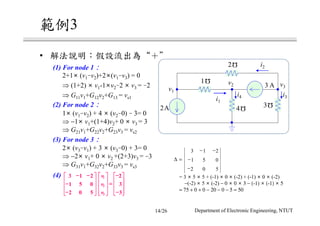
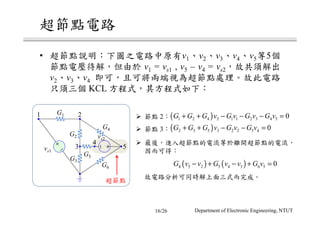
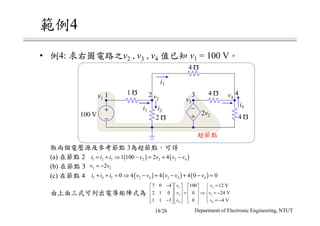
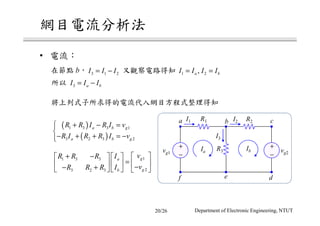
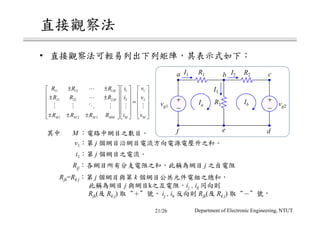
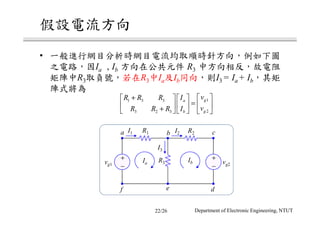
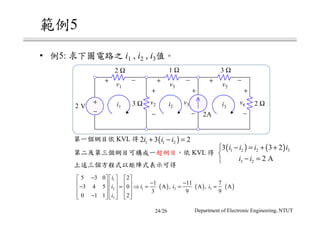
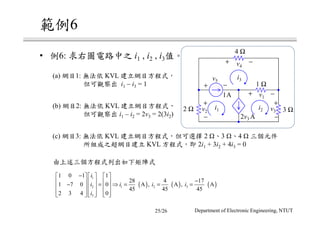
The document discusses different circuit analysis techniques including node voltage analysis, mesh current analysis, and the use of conductance matrices. It provides examples of applying these techniques to solve for unknown voltages and currents in circuits containing multiple nodes and meshes. Key steps include setting up systems of equations using Kirchhoff's laws and the conductance matrix representation of the circuit to solve for the unknown variables. Solutions are obtained using techniques like Cramer's rule.

1. Department of Electronic Engineering
National Taipei University of Technology

2. •
•
• (Node Voltage Analysis)
• (Mesh Current Analysis)
Department of Electronic Engineering, NTUT2/26

3. •
N KVL
N =
Department of Electronic Engineering, NTUT
1 2 Nv v v v= + + +⋯
1 1 2 2, , , N Nv R i v R i v R i= = =⋯
1 2 Nv R i R i R i= + + +⋯
1 2 N
v
i
R R R
=
+ + +⋯
1 2
1
N
s N n
n
R R R R R
=
= + + + = ∑⋯
+
+
−
+
−
+
−
v
i
v1
−
vN
v2
R1
R2
RN
3/26

4. •
N
•
Department of Electronic Engineering, NTUT
1 2
1 2, , , N
N
s s s
RR R
v v v v v v
R R R
= = =⋯
1 2 1 2: : : : : :N Nv v v R R R=⋯ ⋯
+
+
−
+
−
+
−
v
i
v1
−
vN
v2
R1
R2
RN
4/26

5. 1
• 1: i v1 v2 v3 ?
Department of Electronic Engineering, NTUT
(a)(a)(a)(a)
+
−
16 Ω
+
−
6 Ω
+
−
8 Ω
+
−
2 Ω 12 Ω 4 Ω
v1
i
′a
b c
′b ′c
a
v2 v3
( )2
30 Vt
e−
(b)(b)(b)(b)
+
−
+
−
+
−
i
a b
′a ′b
2 Ω 12 Ω
16 Ω 4 Ωv1 v2( )2
30 Vt
e− (a) (b)
5/26

6. 1
Department of Electronic Engineering, NTUT
(b)(b)(b)(b)
+
−
+
−
+
−
i
a b
′a ′b
2 Ω 12 Ω
16 Ω 4 Ωv1 v2( )2
30 Vt
e−
(c)(c)(c)(c)
+
−
+
−
i
a
′a
( )2
30 Vt
e−
2 Ω
8 Ω v1
(b) (c)
• (c) KLC
2
30 2 8 0t
e i i−
− + + =
2
3 t
i e−
=
( )2 2
1
8
30 24 V
2 8
t t
v e e− − 
= ⋅ = 
+ 
( )2
2 1
4
6 V
12 4
t
v v e− 
= ⋅ = 
+ 
( )2
3 2
8
4 V
8 4
t
v v e− 
= ⋅ = 
+ 
6/26

7. • :
N i = i1 + i2 + ... + iN
• R1 R2
Department of Electronic Engineering, NTUT
1 1 2 2, , , N Ni G v i G v i G v= = =⋯
1 2 Ni G v G v G v= + + +⋯
1 2 N
i
v
G G G
=
+ + +⋯
11 2
1 1 1 1 1N
np N nR R R R R=
= + + + = ∑⋯
1 2
1 2
1 2
||eq
R R
R R R
R R
= =
+
+
−
vi G1 G2 GN
i1 i2
iN
7/26

8. •
Department of Electronic Engineering, NTUT
1 2
1 2
1 2
, , ,p p pN
N
p p p N
R R RGG G
i i i i i i i i i
G R G R G R
= = = = = =⋯
1 2 1 2
1 2
1 1 1
: : : : : : : : :N N
N
i i i G G G
R R R
= =⋯ ⋯ ⋯
+
−
vi G1 G2 GN
i1 i2
iN
8/26

9. 2
• 2: i1 i2 ?
Department of Electronic Engineering, NTUT
6 Ω3 Ω
6 Ω 3 Ω 4 Ω 6 Ω
a b
a′ b′
(a)(a)(a)(a)
(A)12
i1 i2
3 Ω
3 Ω3 Ω6 ΩA12
a b
a′ b′
(b)(b)(b)(b)
i1
(a) (b)
9/26

10. 2
Department of Electronic Engineering, NTUT
3 Ω
3 Ω3 Ω6 ΩA12
a b
a′ b′
(b)(b)(b)(b)
i1
a
A12
a′
(c)(c)(c)(c)
6 Ω2 Ω
i1
( )1
2
12 3 A
2 6
i
 
= ⋅ = 
+ 
• (c)
( )2 1
4 3
A
4 6 6 4
i i
 
= ⋅ = 
+ + 
• (a)
10/26

11. (Node Voltage Analysis)
• KCL
•
•
va , vb , vc va , vb , vc
Department of Electronic Engineering, NTUT
a : 1 2 1 0si i i+ − = ( )1 2 1 0a b a sG v v G v i− + − =
1 3 4 0i i i− + + = ( ) ( )1 3 4 0a b b b cG v v G v G v v− − + + − =b :
4 5 2 0si i i− + + = ( )4 5 2 0b c c sG v v G v i− − + + =c :
( )1 2 1 10a b sG G v G v i+ − + =
( )1 1 3 4 4 0a b cG v G G G v G v− + + − =
( )4 4 5 20 b c sG v G G v i− + + = −
is1
a b
d
G2
i2 G3
i3
i5
i4i1
G1 G4 c
is2
G5
11/26

12. •
• G
Department of Electronic Engineering, NTUT
v1 . . . vN N ( )
Gjj j j
Gjk = Gkj , j ≠ k ， j k
j k
ij j
G G G
G G G
G G G
v
v
v
i
i
i
N
N
N N NN N N
11 12 1
21 22 2
1 2
1
2
1
2
−−−− −−−−
−−−− −−−−
−−−− −−−−
























====












......
......
......
......
...
...
...
...
...
12/26

13. 3
• 3: v1 , v2 , v3 , i1 , i2 , i3 , i4
Department of Electronic Engineering, NTUT
Cramer’s rule
A2
3 A
v1
i22
Ω
1
Ω
4
Ω
v2 v3
i3i4
i1
11 3G = ℧ 22 5G = ℧ 33 5G = ℧
12 21 1G G= = ℧
13 31 2G G= = ℧
23 32 2G G= = ℧
1
2
3
3 1 2 2
1 5 0 3
2 0 5 3
v
v
v
− − −    
    − =    
    − −    
3 1 2
1 5 0 50
2 0 5
− −
∆ = − =
−
2
2 1 2
3 5 0 65
3 0 5
− − −
∆ = = −
−
3
3 2 2
1 3 0 17
2 3 5
− −
∆ = − =
− −
4
3 1 2
1 5 3 56
2 0 3
− −
∆ = − = −
− −
1
1 1.3 Vv
∆
= = −
∆
2
2 0.34 Vv
∆
= =
∆
3
3 1.12 Vv
∆
= = −
∆
( )1 1 21 1.64 Ai v v= − = −
( )2 1 21 0.36 Ai v v= − =
3 3.36 Ai = −
4 1.36 Ai =
13/26
Ω
3

14. 3
•
Department of Electronic Engineering, NTUT
= 3 × 5 × 5 + (-1) × 0 × (-2) + (-1) × 0 × (-2)
−(-2) × 5 × (-2) − 0 × 0 × 3 − (-1) × (-1) × 5
= 75 + 0 + 0 − 20 − 0 − 5 = 50
502
051
213
−
−
−−
=∆
(4) 3 1 2
1 5 0
2 0 5
2
3
3
1
2
3
−−−− −−−−
−−−−
−−−−




















====
−−−−
−−−−










v
v
v
(1) For node 1：
2+1× (v1 v2)+2×(v1 v3) = 0
⇒ (1+2) × v1-1×v2 2 × v3 = 2
⇒ G11v1+G12v2+G13 = vs1
(2) For node 2：
1× (v1 v2) + 4 × (v2 0) 3= 0
⇒ −1× v1+(1+4)v2+ 0 × v3 = 3
⇒ G21v1+G22v2+G23v3 = vs2
(3) For node 3：
2× (v3 v1) + 3 × (v3 0) + 3= 0
⇒ −2× v1+ 0 × v2 +(2+3)v3 = 3
⇒ G31v1+G32v2+G33v3 = vs3
A2
3 A
v1
i22
Ω
1
Ω
4
Ω
v2 v3
i3i4
i1
14/26
Ω
3

15. •
M (M-1)
(M-1) (M-1)
(Supernode)
KCL
Department of Electronic Engineering, NTUT15/26

16. • v1 v2 v3 v4 v5 5
v1 = vs1 , v5 – v4 = vs2
v2 v3 v4
KCL
Department of Electronic Engineering, NTUT
2
3
( )1 2 4 2 1 1 2 3 4 5 0G G G v G v G v G v+ + − − − =
( )2 3 5 3 2 2 5 4 0G G G v G v G v+ + − − =
( ) ( )4 5 2 5 4 3 6 5 0G v v G v v G v− + − + =
+
−
1 2
3
4
5vs1
G1
G4
G6
G5
G3
G2 vs2
16/26

17. •
KVL
KCL
KCL
1 2 3 KCL ( )
Department of Electronic Engineering, NTUT
+
−
1 2
3
44 sv v=
( )1 2 3 1 2 2 3 3 1 0sG G G v G v G v G v+ + − − − =
( ) ( )2 1 2 5 2 1 3 0G v G G v v vβ− + + + − =
( ) ( )3 1 3 4 3 1 3 0G v G G v v vβ− + + − − =
vs
G1 G2
G3
G4
( )1 3v vβ −
G5
17/26

18. 4
• 4: v2 , v3 , v4 v1 = 100 V
Department of Electronic Engineering, NTUT
3
(a) 2
(b) 3
(c) 4
( ) ( )1 2 3 2 2 2 41 100 2 4i i i v v v v= + ⇒ − = + −
3 22v v= −
( ) ( ) ( )3 4 5 2 4 3 4 40 4 4 4 0 0i i i v v v v v+ + = ⇒ − + − + − =
2 2
3 3
4 4
7 0 4 100 12 V
2 1 0 0 24 V
1 1 3 0 4 V
v v
v v
v v
− =      
     = ⇒ = −     
     − = −      
+
−
+
−
1
Ω
4
32
V100
4v1
Ω
1
Ω
4
Ω
4
Ω
2
2v2
v3
v4
i5i1 i2
v2
i3
18/26

19. (Mesh Current Analysis)
•
KVL
IR
KVL
• 2 2
Ia Ib KVL
Department of Electronic Engineering, NTUT
1 (a-b-e-f-a) ⇒
2 (b-c-d-e-b) ⇒
+
−
+
−
vg1
a b c
def
I1
vg2
I2
I3
R1
R3
R2
Ia Ib
1 1 1 3 3 0gv I R I R− + + =
3 3 2 2 2 0gI R I R v− + + =
1 1 3 3 1gI R I R v+ =
2 2 3 3 2gI R I R v+ =
19/26

20. •
Department of Electronic Engineering, NTUT
b
+
−
+
−
vg1
a b c
def
I1
vg2
I2
I3
R1
R3
R2
Ia Ib
3 1 2I I I= − 1 2,a bI I I I= =
3 a bI I I= −
( )
( )
1 3 3 1
3 2 3 2
a b g
a b g
R R I R I v
R I R R I v
 + − =

− + + = −
11 3 3
23 2 3
ga
gb
vR R R I
vR R R I
+ −     
=      −− +     
20/26

21. •
Department of Electronic Engineering, NTUT
M
v1 j
i1 j
Rjj j
Rjk=Rk j j k
j k ij , ik
Rjk( Rk j) ij , ik Rjk( Rk j) 。
+
−
+
−
vg1
a b c
def
I1
vg2
I2
I3
R1
R3
R2
Ia Ib
11 12 1 1 1
21 22 2 2 2
1 2 3
M
M
M M M MM M M
R R R i v
R R R i v
R R R R i v
± ±     
     ± ±
     =
     
     
± ± ±     
⋯
⋯
⋮ ⋮ ⋱ ⋮ ⋮ ⋮
21/26

22. •
Ia , Ib R3
R3 R3 Ia Ib I3 = Ia + Ib
Department of Electronic Engineering, NTUT
+
−
+
−
vg1
a b c
def
I1
vg2
I2
I3
R1
R3
R2
Ia Ib
11 3 3
23 2 3
ga
gb
vR R R I
vR R R I
+     
=     +     
22/26

23. •
KVL
Department of Electronic Engineering, NTUT23/26

24. 5
• 5: i1 , i2 , i3
Department of Electronic Engineering, NTUT
KVL
KVL
+
−
V2
2 Ω 1 Ω 3 Ω
2 Ω
+
−
+ −
A2
+
−
+
−
3 Ω
+ −+ −
v1 v3 v5
v3v2 v6i1 i2 i3
( )1 1 22 3 2i i i+ − =
( ) ( )1 2 2 3
3 2
3 3 2
2 A
i i i i
i i
 − = + +

− =
( ) ( ) ( )
1
2 1 2 3
3
5 3 0 2
1 11 7
3 4 5 0 A , A , A
3 9 9
0 1 1 2
i
i i i i
i
−     
− −    − = ⇒ = = =    
    −    
24/26

25. 6
• 6: i1 , i2 , i3
Department of Electronic Engineering, NTUT
(a) 1: KVL
i1 – i3 = 1
(b) 2: KVL
i1 – i2 = 2v3 = 2(3i2)
(c) 3: KVL 2 3 4
KVL 2i1 + 3i2 + 4i3 = 0
4 Ω
+ −
A1
+
−
+
−
+ −
+ −
v4
2 Ω 3 Ω
v5
v2
v1
v3
1 Ω
i3
i1 i2
2v3 A
( ) ( ) ( )
1
2 1 2 3
3
1 0 1 1
28 4 17
1 7 0 0 A , A , A
45 45 45
2 3 4 0
i
i i i i
i
−     
−    − = ⇒ = = =    
        
25/26

26. •
(KCL)
(KVL)
•
•
( ) ( )
Department of Electronic Engineering, NTUT26/26