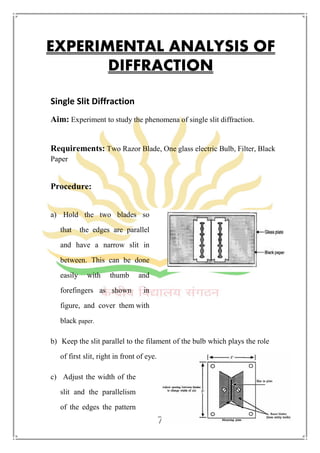
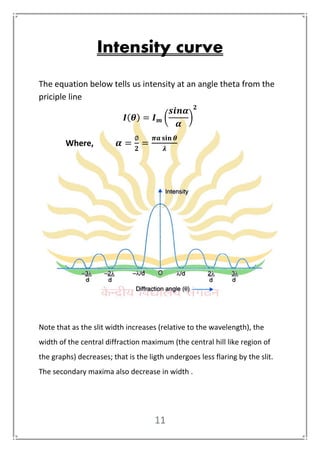
The document is an investigatory project on diffraction, exploring its intensity curve, authored by Saurabh Yadav under the guidance of Mr. Gaurav Agarwal. It covers the concepts of diffraction, types including Fresnel and Fraunhofer diffraction, and includes experimental analyses of single slit diffraction and diffraction by circular apertures. Additionally, it provides information on the dependence of diffraction patterns on wavelength and includes a bibliography for further reading.

1. PHYSICS INVESTIGATORY
PROJECT
ON
“To study Diffraction and
Explain its intensity curve”
PREPARED BY:- GUIDED BY:-
Saurabh Yadav Mr. Gaurav Agarwal
Class: XII
Roll No.

2. 2
ACKNOWLEDGEMENT
It is my foremost duty to express my deep regards to
my Physics teacher Mr. Gaurav Agarwal under
whose guidance and supervision I am able to
undertake this project. It is he who has been my
primary source of inspiration and who motivated,
guided and encouraged me at different stages to make
this project. I am also thankful for the help rendered
by our lab teacher who made available the various
apparatus and chemicals needed for the experiments,
else it would have been a difficult task to perform this
project successfully. I also want to thank the lab
attendant for their invaluable help.
Saurabh Yadav
2019-20

3. 3
CERTIFICATE
This to certify that “Saurabh Yadav” of class
XII bearing roll no- who is going to
appear for AISSCE-2020 has successfully
completed all the practicals and projects in
Chemistry during the session 2019-2020 as
per the prescribed syllabus of C.B.S.E., New
Delhi.
Internal Examiner:__________ Principal:__________
External Examiner:__________ Date:__________

4. 4
Contents
Introduction
Types of Diffraction
Experimental Analysis
Single Slit Diffraction
Diffraction by Circular Aperture
Intensity Curve
Bibiliography

5. 5
Introduction
Diffraction refers to various phenomena that occur when a wave
encounters an obstacle or a slit. It is defined as the bending of waves
around the corners of an obstacle or through an aperture into the
region of geometrical shadow of the obstacle/aperture. The
diffracting object or aperture effectively becomes a secondary source
of the propagating wave. Italian scientist Francesco Maria Grimaldi
coined the word "diffraction" and was the first to record accurate
observations of the phenomenon in 1660.
In classical physics, the diffraction phenomenon is described by the
Huygens–Fresnel principle that treats each point in a propagating
wave-front as a collection of individual spherical wavelets. The
characteristic banding pattern is most pronounced when a wave
from a coherent source (such as a laser) encounters a slit/aperture
that is comparable in size to its wavelength, as shown in the inserted
image. This is due to the addition, or interference, of different points
on the wave-front (or, equivalently, each wavelet) that travel by
paths of different lengths to the registering surface. However, if there
are multiple, closely spaced openings, a complex pattern of varying
intensity can result.
Diffraction and interference are closely related and are nearly – if not
exactly – identical in meaning. Richard Feynman observes that
"diffraction" tends to be used when referring to many wave sources,
and "interference" when only a few are considered.
The effects of diffraction are often seen in everyday life. The most
striking examples of diffraction are those that involve light; for
example, the closely spaced tracks on a CD or DVD act as a
diffraction grating to form the familiar rainbow pattern seen when
looking at a disc. This principle can be extended to engineer a
grating with a structure such that it will produce any diffraction
pattern desired; the hologram on a credit card is an example.

6. Types of Diffraction
There are two ways in which analysis of diffraction of light is done which are
given below :
1. Fresenel Diffraction:
When diffraction of light is analysed for a light source at finite distance
from the diffracting device and point of observation or screen is also
located at finite distance from the device as show in figure 6.73, then in
such conditions mostly the diffraction analysis is done with some specific
methods called as “Fresnel’s Diffraction”.
2. Fraunhoffer Diffraction:
When diffraction is analysed for a source at very large distance from the
diffracting device and point of observation or screen is also at very large
distance from the device as shown in figure 6.74, then in such conditions
mostly the diffraction analysis is done with some specific methods called
as “Fraunhoffer Diffraction”

7. EXPERIMENTAL ANALYSIS OF
DIFFRACTION
Single Slit Diffraction
Aim: Experiment to study the phenomena of single slit diffraction.
Requirements: Two Razor Blade, One glass electric Bulb, Filter, Black
Paper
Procedure:
a) Hold the two blades so
that the edges are parallel
and have a narrow slit in
between. This can be done
easily with thumb and
forefingers as shown in
figure, and cover them with
black paper.
b) Keep the slit parallel to the filament of the bulb which plays the role
of first slit, right in front of eye.
c) Adjust the width of the
slit and the parallelism
of the edges the pattern

8. the pattern of light and
dark bands is visible.
d) As the position of the bands (except the central one) depends on the
wavelength, they will show some colours. e) Use a filter for red and blue to
make fringes clearer, Compare the fringes.
Observations: Since the
position of all the bands
depends on wavelength so they
will show some colour. More
the wavelength, More they will
diffract. Result: Fringes are
wider for red
compared to blue.
Precaution: Protect your eyes by using spectacles while performing the
experiment. Don’t use sunlight instead of the bulb as sun also produces
infrared rays harmful to our eyes.
*By repeating the above experiment with aluminium foil we can easily
show double slit diffraction.*

10. To produce the first dark fringe they must be out of phase by l/2 when they
reach at P1.
This pahse difference is due to path
length difference travelled by wavelets.
Therefore the above result can be generalised for every dark fringe as :
Diffraction by Circular Aperture
Here we consider diffraction by a circular aperture that is a
circular opening, such as circular lens through which light can
pass. Figure 36.10 shows the image formed by light from a laser
that was directed onto a circular aperture with a very small
diameter. This image is not apoint as geometrical optics would
suggest but a circular disk surrounded by several progressively
fainter secondary rings.
The analysis of such patterns shows that the first minimum for the
diffraction pattern of a circular aperture of diameter d is located by
The angle theta is the angle from the central axis to any point on that
circular minimum.

11. Intensity curve
The equation below tells us intensity at an angle theta from the
priciple line
Where,
∅
Note that as the slit width increases (relative to the wavelength), the
width of the central diffraction maximum (the central hill like region of
the graphs) decreases; that is the ligth undergoes less flaring by the slit.
The secondary maxima also decrease in width .

12. Bibiliography
Websites:
1.www.wikipedia .org
2.www.physics.usyd.edu.au
Books:
1.Physics Galaxy (Book)
2.Comprehensive Practical Guide (Book)
3.Fundamental Of Physics (Halliday
&Resnick)