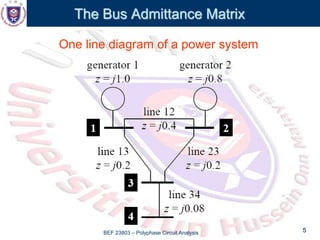
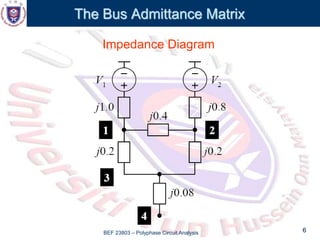
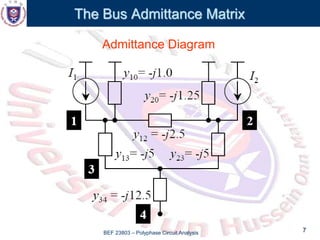
This document discusses the admittance and impedance bus models used in power flow analysis. It outlines the bus admittance matrix method for relating nodal voltages to branch currents using the admittance values. The bus admittance matrix is a square matrix with dimensions equal to the number of buses. Node elimination methods like Kron reduction can be used to reduce the matrix by eliminating buses with no current injection. The document provides an example of applying Kron reduction to eliminate a node from the bus admittance matrix.

1. BEF 23803
Polyphase Circuit Analysis
Chapter 5
The Admittance and Impedance Model

2. BEF 23803 – Polyphase Circuit Analysis 2
Outlines
 Introduction
 The Bus Admittance Matrix
 Power Flow Methods
– Gaussian Elimination
– Kron Reduction
 The Bus Impedance Matrix

3. BEF 23803 – Polyphase Circuit Analysis 3
Introduction
 The knowledge of admittance and impedance bus
construction are essential in power flow study.
 In general, each of power system network consist of
several buses:
 Load Bus or PQ Bus
– known real (P) and reactive (Q) power injections.
– No generator attach to load bus.
 Generator Bus or PV Bus
– known real (P) power injection and the voltage
magnitude (V).
 Slack Bus or Swing Bus
– known voltage magnitude (V) and voltage angle (),
often it is taken to be 10 p.u.
– must have one generator as the slack bus.
– takes up the power slack due to losses in the network.

4. BEF 23803 – Polyphase Circuit Analysis 4
The Bus Admittance Matrix
 The matrix equation for relating the nodal voltages
to the currents that flow into and out of a network
using the admittance values of circuit branches.
V1
Vi
Ii
yi1
yi2
yin
…
yi0
V2
Vn
Iinj = YbusVnode
ij
ij
ij
ij
jx
r
z
y



1
1






































n
nn
n
n
n
n
n V
V
V
Y
Y
Y
Y
Y
Y
Y
Y
Y
I
I
I









2
1
2
1
2
22
21
1
12
11
2
1

5. BEF 23803 – Polyphase Circuit Analysis 5
The Bus Admittance Matrix
One line diagram of a power system

6. BEF 23803 – Polyphase Circuit Analysis 6
The Bus Admittance Matrix
Impedance Diagram

7. BEF 23803 – Polyphase Circuit Analysis 7
The Bus Admittance Matrix
Admittance Diagram

8. BEF 23803 – Polyphase Circuit Analysis 8
The Bus Admittance Matrix
Kirchhoff’s current law:

9. BEF 23803 – Polyphase Circuit Analysis 9
The Bus Admittance Matrix
Rearranging the KCL Equations:
Matrix Formation of the Equations:

10. BEF 23803 – Polyphase Circuit Analysis 10
The Bus Admittance Matrix
Completed Matrix Equation:






































n
nn
n
n
n
n
n V
V
V
Y
Y
Y
Y
Y
Y
Y
Y
Y
I
I
I









2
1
2
1
2
22
21
1
12
11
2
1
bus
bus
bus V
Y
I .


11. BEF 23803 – Polyphase Circuit Analysis 11
Y-Bus Matrix Building Rules
 Square matrix with dimensions equal to the number of buses.
 Convert all network impedances into admittances.
 Diagonal elements:
 Off-diagonal elements:
 Matrix is symmetrical along the leading diagonal.
 When the bus currents are known,
bus
bus
bus I
Y
V 1



12. BEF 23803 – Polyphase Circuit Analysis 12
Node Elimination (Kron Reduction)
 Current injection is always zero at busses of network which there is no
external load or generating source connected.
 It is usually not necessary to calculate the voltage at that bus, thus can
be eliminated from the system representation.
 System in which nodes with zero current injection are eliminated is said
to be Kron Reduced.
 For the nodal equation of N bus system, the elements of new reduced
bus admittance can be calculated using
pp
pk
jp
jk
new
jk
Y
Y
Y
Y
Y 

)
(
Where
j and k are the integer value from 1 to N except p
since row p and column p are going to eliminated.
p = node to eliminated.

13. BEF 23803 – Polyphase Circuit Analysis 13
Node Elimination (Kron Reduction)
Example
 Find the Ybus new using Kron Reduction method when node 2 for the
network given by nodal admittance equation in matrix form below is
removed.















































135
68
.
0
90
00
.
1
0
0
30
.
8
00
.
0
00
.
5
5
.
2
00
.
0
80
.
5
5
.
2
5
.
2
00
.
5
50
.
2
25
.
19
75
.
11
50
.
2
50
.
2
75
.
11
75
.
16
4
3
2
1
V
V
V
V
j
j
j
j
j
j
j
j
j
j
j
j
j
j

14. BEF 23803 – Polyphase Circuit Analysis 14
Node Elimination (Kron Reduction)
Example Solution
 The new row one elements after node 2 is eliminated
pu
j
j
j
j
j
Y
Y
Y
Y
Y new 57792
.
9
25
.
19
)
75
.
11
)(
75
.
11
(
25
.
16
22
21
12
11
)
(
11 







pu
j
j
j
j
j
Y
Y
Y
Y
Y new 02957
.
4
25
.
19
)
50
.
2
)(
75
.
11
(
50
.
2
22
23
12
13
)
(
13 





pu
j
j
j
j
j
Y
Y
Y
Y
Y new 55195
.
5
25
.
19
)
00
.
5
)(
75
.
11
(
5
.
2
22
24
12
14
)
(
14 






15. BEF 23803 – Polyphase Circuit Analysis 15
Node Elimination (Kron Reduction)
Example Solution
 Similar calculation for the next row would give








































135
68
.
0
90
00
.
1
0
00130
.
7
64935
.
0
55195
.
5
64935
.
0
47532
.
5
02597
.
4
55195
.
5
02597
.
4
7791
.
9
4
3
1
V
V
V
j
j
j
j
j
j
j
j
j